Sub-exponential Growth of New Words and Names Online: A Piecewise Power-Law Model

The diffusion of ideas and language in society has conventionally been described by S-shaped models, such as the logistic curve. However, the role of sub-exponential growth -- a slower-than-exponential pattern known in epidemiology -- has been largely overlooked in broader social phenomena. Here, we present a piecewise power-law model to characterize complex growth curves with a few parameters. We systematically analyzed a large-scale dataset of approximately one billion Japanese blog articles linked to Wikipedia vocabulary, and observed consistent patterns in web search trend data (English, Spanish, and Japanese). Our analysis of 2,963 items, selected for reliable estimation (e.g., sufficient duration/peak, monotonic growth), reveals that 1,625 (55%) diffusion patterns without abrupt level shifts were adequately described by one or two segments. For single-segment curves, we found that (i) the mode of the shape parameter $α$ was near 0.5, indicating prevalent sub-exponential growth; (ii) the peak diffusion scale is primarily determined by the growth rate $R$, with minor contributions from $α$ or the duration $T$; and (iii) $α$ showed a tendency to vary with the nature of the topic, being smaller for niche/local topics and larger for widely shared ones. Furthermore, a micro-behavioral model of outward (stranger) vs. inward (community) contact suggests that $α$ can be interpreted as an index of the preference for outward-oriented communication. These findings suggest that sub-exponential growth is a common pattern of social diffusion, and our model provides a practical framework for consistently describing, comparing, and interpreting complex and diverse growth curves.

A minor extension of the logistic equation for growth of word counts on online media: Parametric description of diversity of growth phenomena in society

To understand the growing phenomena of new vocabulary on nationwide online social media, we analyzed monthly word count time series extracted from approximately 1 billion Japanese blog articles from 2007 to 2019. In particular, we first introduced the extended logistic equation by adding one parameter to the original equation and showed that the model can consistently reproduce various patterns of actual growth curves, such as the logistic function, linear growth, and finite-time divergence. Second, by analyzing the model parameters, we found that the typical growth pattern is not only a logistic function, which often appears in various complex systems, but also a nontrivial growth curve that starts with an exponential function and asymptotically approaches a power function without a steady state. Furthermore, we observed a connection between the functional form of growth and the peak-out. Finally, we showed that the proposed model and statistical properties are also valid for Google Trends data (English, French, Spanish, and Japanese), which is a time series of the nationwide popularity of search queries.

Empirical observations of ultraslow diffusion driven by the fractional dynamics in languages: Dynamical statistical properties of word counts of already popular words

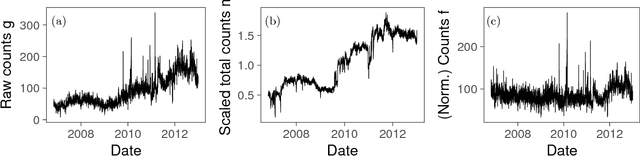
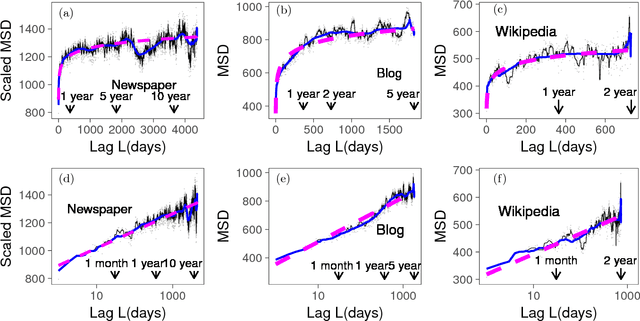
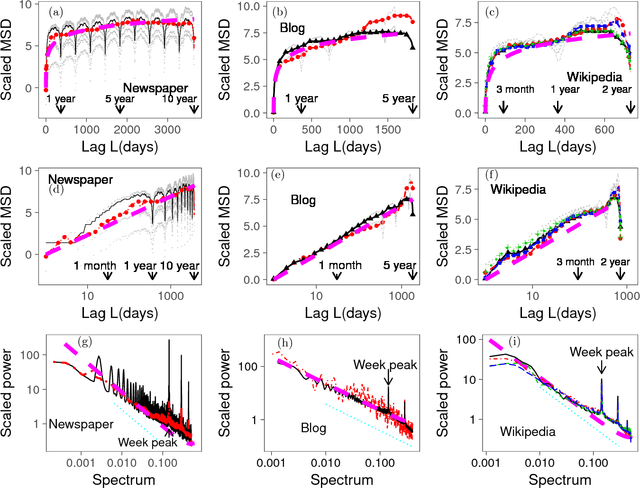
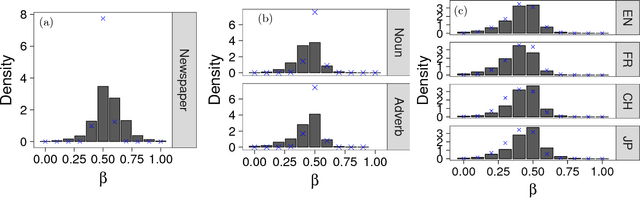
Ultraslow diffusion (i.e. logarithmic diffusion) has been extensively studied theoretically, but has hardly been observed empirically. In this paper, firstly, we find the ultraslow-like diffusion of the time-series of word counts of already popular words by analysing three different nationwide language databases: (i) newspaper articles (Japanese), (ii) blog articles (Japanese), and (iii) page views of Wikipedia (English, French, Chinese, and Japanese). Secondly, we use theoretical analysis to show that this diffusion is basically explained by the random walk model with the power-law forgetting with the exponent $\beta \approx 0.5$, which is related to the fractional Langevin equation. The exponent $\beta$ characterises the speed of forgetting and $\beta \approx 0.5$ corresponds to (i) the border (or thresholds) between the stationary and the nonstationary and (ii) the right-in-the-middle dynamics between the IID noise for $\beta=1$ and the normal random walk for $\beta=0$. Thirdly, the generative model of the time-series of word counts of already popular words, which is a kind of Poisson process with the Poisson parameter sampled by the above-mentioned random walk model, can almost reproduce not only the empirical mean-squared displacement but also the power spectrum density and the probability density function.

Ultraslow diffusion in language: Dynamics of appearance of already popular adjectives on Japanese blogs

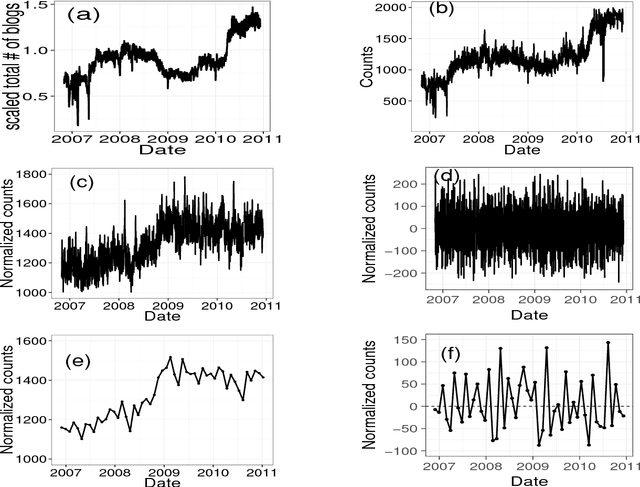
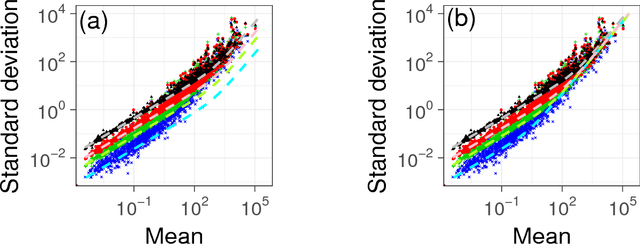
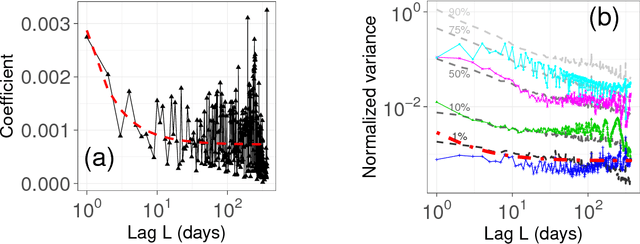
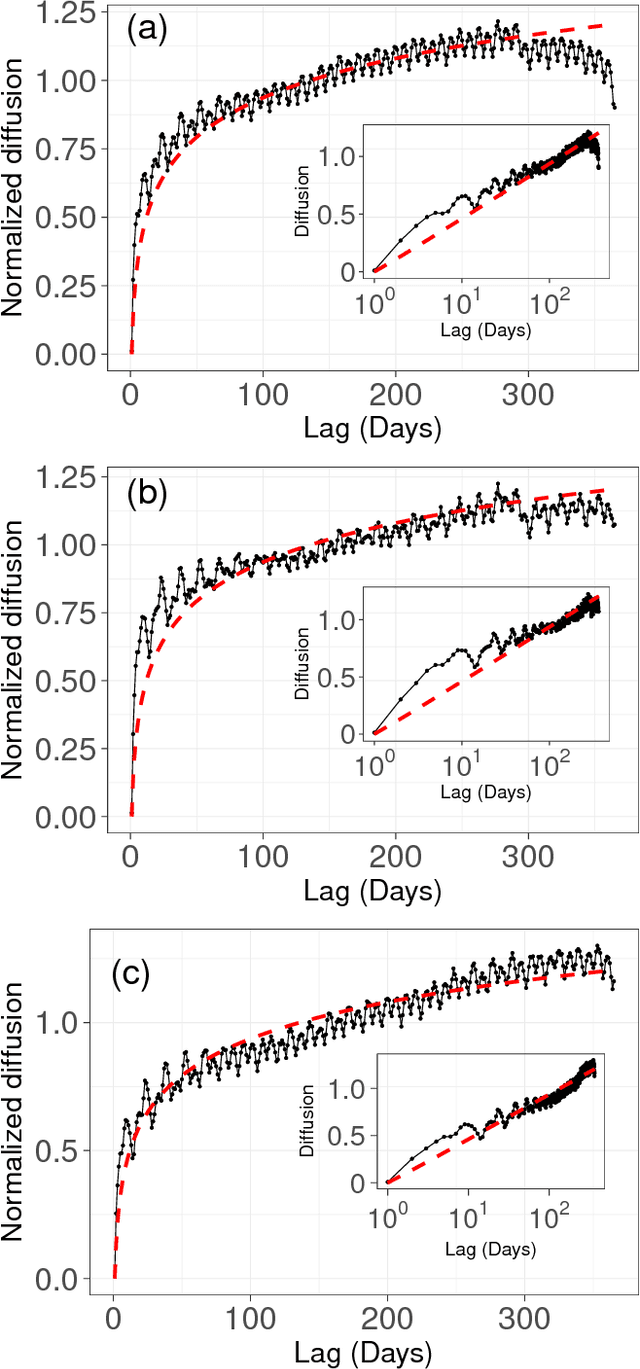
What dynamics govern a time series representing the appearance of words in social media data? In this paper, we investigate an elementary dynamics, from which word-dependent special effects are segregated, such as breaking news, increasing (or decreasing) concerns, or seasonality. To elucidate this problem, we investigated approximately three billion Japanese blog articles over a period of six years, and analysed some corresponding solvable mathematical models. From the analysis, we found that a word appearance can be explained by the random diffusion model based on the power-law forgetting process, which is a type of long memory point process related to ARFIMA(0,0.5,0). In particular, we confirmed that ultraslow diffusion (where the mean squared displacement grows logarithmically), which the model predicts in an approximate manner, reproduces the actual data. In addition, we also show that the model can reproduce other statistical properties of a time series: (i) the fluctuation scaling, (ii) spectrum density, and (iii) shapes of the probability density functions.