Hans R. G. W. Verstraete
Online Optimization with Costly and Noisy Measurements using Random Fourier Expansions
Sep 29, 2016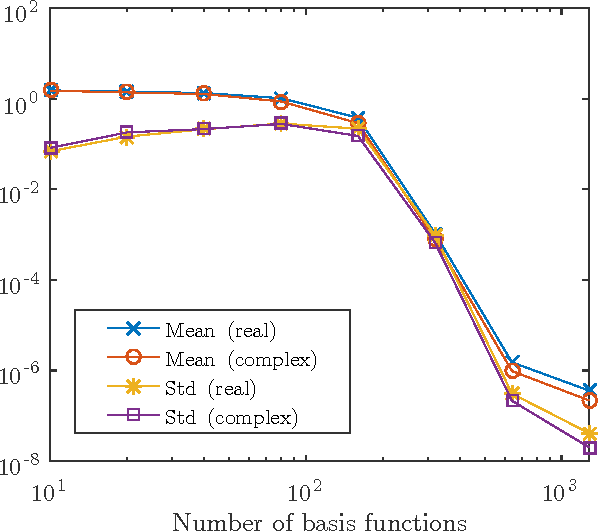
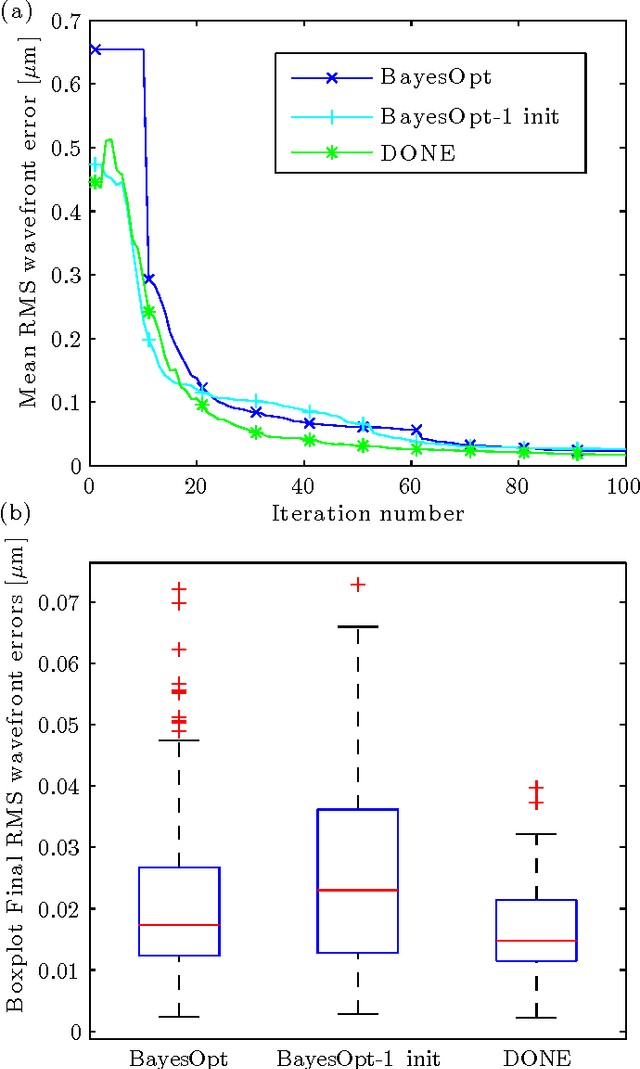
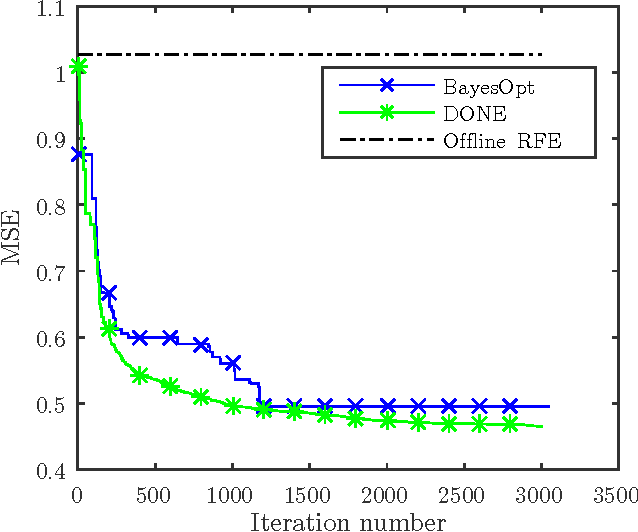
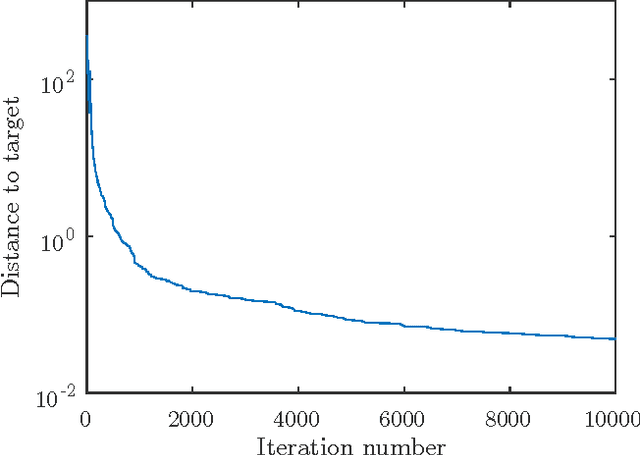
Abstract:This paper analyzes DONE, an online optimization algorithm that iteratively minimizes an unknown function based on costly and noisy measurements. The algorithm maintains a surrogate of the unknown function in the form of a random Fourier expansion (RFE). The surrogate is updated whenever a new measurement is available, and then used to determine the next measurement point. The algorithm is comparable to Bayesian optimization algorithms, but its computational complexity per iteration does not depend on the number of measurements. We derive several theoretical results that provide insight on how the hyper-parameters of the algorithm should be chosen. The algorithm is compared to a Bayesian optimization algorithm for a benchmark problem and three applications, namely, optical coherence tomography, optical beam-forming network tuning, and robot arm control. It is found that the DONE algorithm is significantly faster than Bayesian optimization in the discussed problems, while achieving a similar or better performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge