Learning polycrystal plasticity using mesh-based subgraph geometric deep learning

Polycrystal plasticity in metals is characterized by nonlinear behavior and strain hardening, making numerical models computationally intensive. We employ Graph Neural Network (GNN) to surrogate polycrystal plasticity from finite element method (FEM) simulations. We present a novel message-passing GNN that encodes nodal strain and edge distances between FEM mesh cells, aggregates them to obtain embeddings, and combines the decoded embeddings with the nodal strains to predict stress tensors on graph nodes. We demonstrate training GNN based on subgraphs generated from FEM mesh-graphs, in which the mesh cells are converted to nodes and edges are created between adjacent cells. The GNN is trained on 72 graphs and tested on 18 graphs. We apply the trained GNN to periodic polycrystals and learn the stress-strain maps based on strain-gradient plasticity theory. The GNN is accurately trained based on FEM graphs, in which the $R^2$ for both training and testing sets are 0.993. The proposed GNN plasticity constitutive model speeds up more than 150 times compared with the benchmark FEM method on randomly selected test polycrystals. We also apply the trained GNN to 30 unseen FEM simulations and the GNN generalizes well with an overall $R^2$ of 0.992. Analysis of the von Mises stress distributions in polycrystals shows that the GNN model accurately learns the stress distribution with low error. By comparing the error distribution across training, testing, and unseen datasets, we can deduce that the proposed model does not overfit and generalizes well beyond the training data. This work is expected to pave the way for using graphs as surrogates in polycrystal plasticity modeling.

Inferring micro-bubble dynamics with physics-informed deep learning

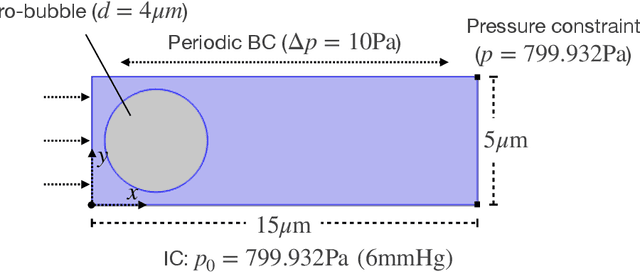
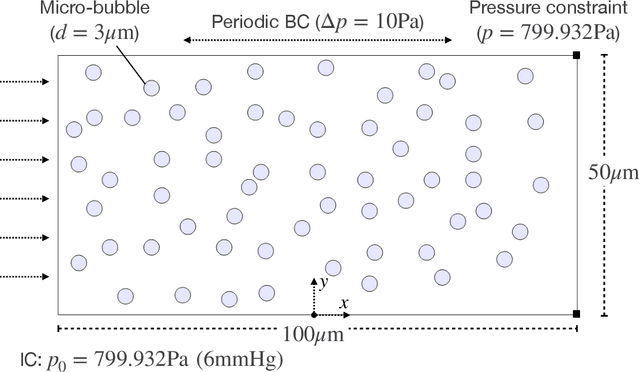
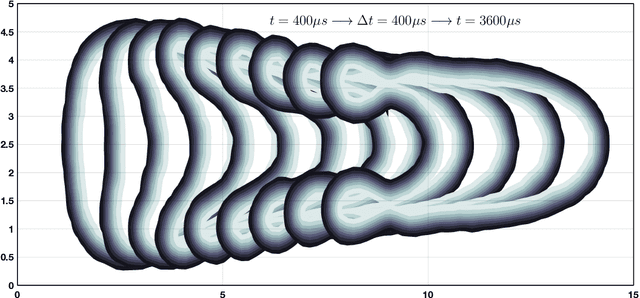
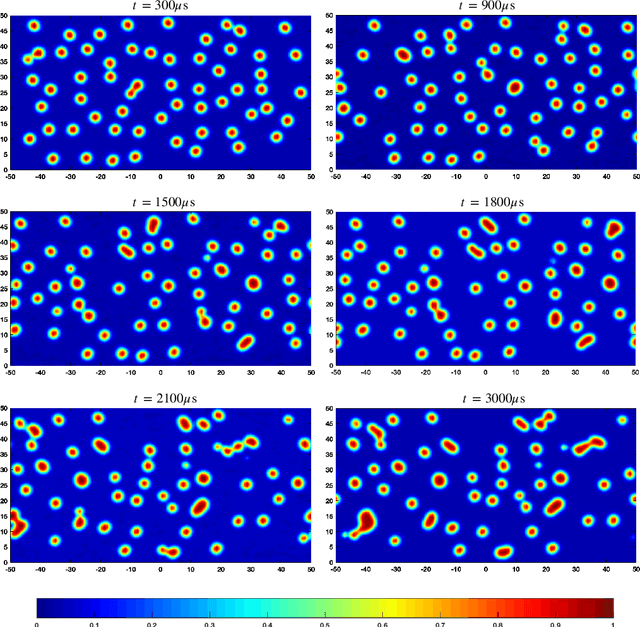
Micro-bubbles and bubbly flows are widely observed and applied to medicine, involves deformation, rupture, and collision of bubbles, phase mixture, etc. We study bubble dynamics by setting up two numerical simulation cases: bubbly flow with a single bubble and multiple bubbles, both confined in the microtube, with parameters corresponding to their medical backgrounds. Both the cases have their medical background applications. Multiphase flow simulation requires high computation accuracy due to possible component losses that may be caused by sparse meshing during the computation. Hence, data-driven methods can be adopted as a useful tool. Based on physics-informed neural networks (PINNs), we propose a novel deep learning framework BubbleNet, which entails three main parts: deep neural networks (DNN) with sub nets for predicting different physics fields; the physics-informed part, with the fluid continuum condition encoded within; the time discretized normalizer (TDN), an algorithm to normalize field data per time step before training. We apply the traditional DNN and our BubbleNet to train the simulation data and predict the physics fields of both the two bubbly flow cases. Results indicate our framework can predict the physics fields more accurately, estimating the prediction absolute errors. The proposed network can potentially be applied to many other engineering fields.