Solving the Encoding Bottleneck: Of the HHL Algorithm, By the HHL Algorithm

The Harrow-Hassidim-Lloyd (HHL) algorithm offers exponential speedup for solving the quantum linear-system problem. But some caveats for the speedup could be hard to met. One of the difficulties is the encoding bottleneck, i.e., the efficient preparation of the initial quantum state. To prepare an arbitrary $N$-dimensional state exactly, existing state-preparation approaches generally require a runtime of $O(N)$, which will ruin the speedup of the HHL algorithm. Here we show that the states can be prepared approximately with a runtime of $O(poly(\log N))$ by employing a slightly modified version of the HHL algorithm itself. Thus, applying this approach to prepare the initial state of the original HHL algorithm can preserve the exponential speedup advantage. It can also serve as a standalone solution for other applications demanding rapid state preparation.

Training quantum machine learning model on cloud without uploading the data

Based on the linearity of quantum unitary operations, we propose a method that runs the parameterized quantum circuits before encoding the input data. It enables a dataset owner to train machine learning models on quantum cloud computation platforms, without the risk of leaking the information of the data. It is also capable of encoding a huge number of data effectively at a later time using classical computations, thus saving the runtime on quantum computation devices. The trained quantum machine learning model can be run completely on classical computers, so that the dataset owner does not need to have any quantum hardware, nor even quantum simulators. Moreover, the method can mitigate the encoding bottom neck by reducing the required circuit depth from $O(2^{n})$ to $n/2$. These results manifest yet another advantage of quantum and quantum-inspired machine learning models over existing classical neural networks, and broaden the approaches for data security.

Computing the gradients with respect to all parameters of a quantum neural network using a single circuit

When computing the gradients of a quantum neural network using the parameter-shift rule, the cost function needs to be calculated twice for the gradient with respect to a single adjustable parameter of the network. When the total number of parameters is high, the quantum circuit for the computation has to be adjusted and run for many times. Here we propose an approach to compute all the gradients using a single circuit only, with a much reduced circuit depth and less classical registers. We also demonstrate experimentally, on both real quantum hardware and simulator, that our approach has the advantages that the circuit takes a significantly shorter time to compile than the conventional approach, resulting in a speedup on the total runtime.

Collaboration between parallel connected neural networks -- A possible criterion for distinguishing artificial neural networks from natural organs

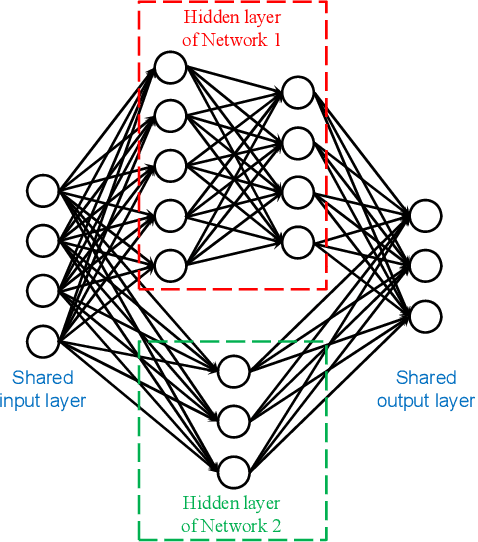
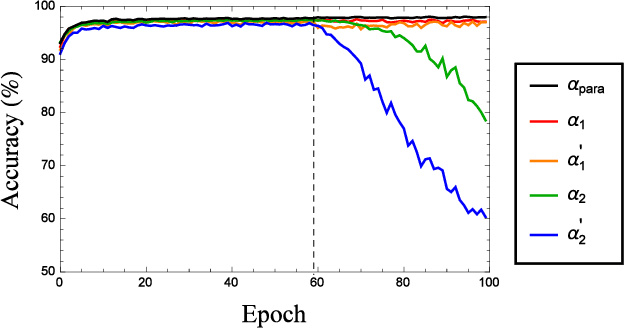
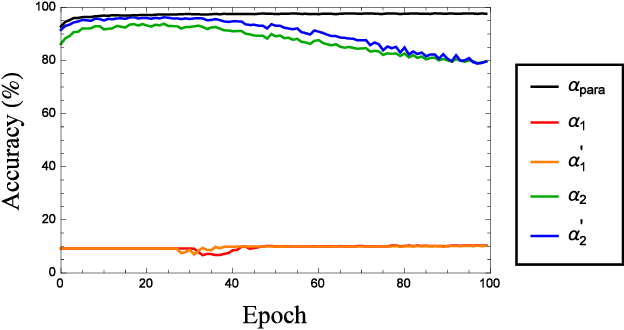
We find experimentally that when artificial neural networks are connected in parallel and trained together, they display the following properties. (i) When the parallel-connected neural network (PNN) is optimized, each sub-network in the connection is not optimized. (ii) The contribution of an inferior sub-network to the whole PNN can be on par with that of the superior sub-network. (iii) The PNN can output the correct result even when all sub-networks give incorrect results. These properties are unlikely for natural biological sense organs. Therefore, they could serve as a simple yet effective criterion for measuring the bionic level of neural networks. With this criterion, we further show that when serving as the activation function, the ReLU function can make an artificial neural network more bionic than the sigmoid and Tanh functions do.