Adapting Noise to Data: Generative Flows from 1D Processes

We introduce a general framework for constructing generative models using one-dimensional noising processes. Beyond diffusion processes, we outline examples that demonstrate the flexibility of our approach. Motivated by this, we propose a novel framework in which the 1D processes themselves are learnable, achieved by parameterizing the noise distribution through quantile functions that adapt to the data. Our construction integrates seamlessly with standard objectives, including Flow Matching and consistency models. Learning quantile-based noise naturally captures heavy tails and compact supports when present. Numerical experiments highlight both the flexibility and the effectiveness of our method.

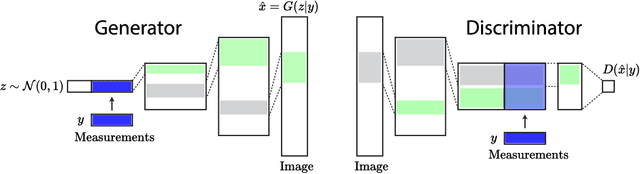
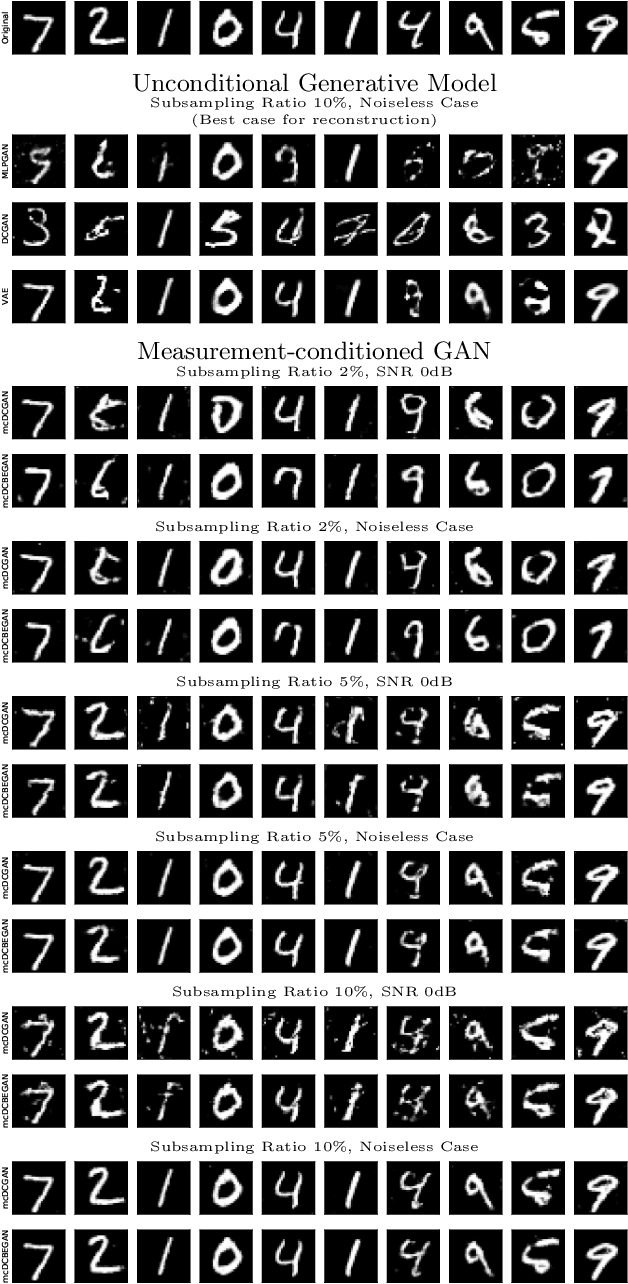
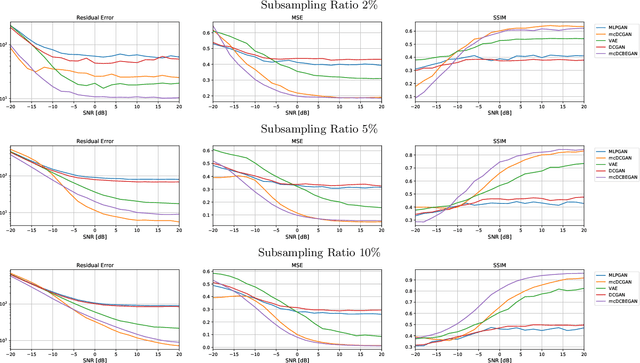
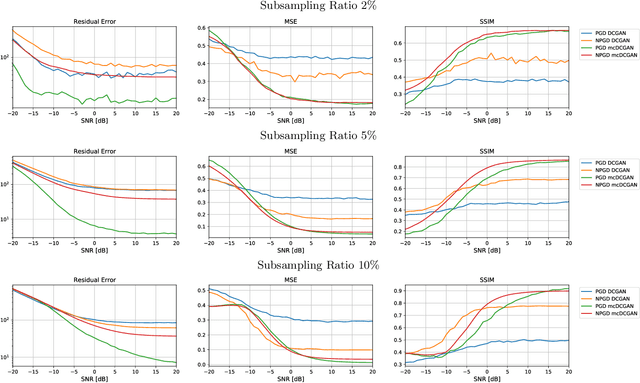
Solving Inverse Problems with Conditional-GAN Prior via Fast Network-Projected Gradient Descent

The projected gradient descent (PGD) method has shown to be effective in recovering compressed signals described in a data-driven way by a generative model, i.e., a generator which has learned the data distribution. Further reconstruction improvements for such inverse problems can be achieved by conditioning the generator on the measurement. The boundary equilibrium generative adversarial network (BEGAN) implements an equilibrium based loss function and an auto-encoding discriminator to better balance the performance of the generator and the discriminator. In this work we investigate a network-based projected gradient descent (NPGD) algorithm for measurement-conditional generative models to solve the inverse problem much faster than regular PGD. We combine the NPGD with conditional GAN/BEGAN to evaluate their effectiveness in solving compressed sensing type problems. Our experiments on the MNIST and CelebA datasets show that the combination of measurement conditional model with NPGD works well in recovering the compressed signal while achieving similar or in some cases even better performance along with a much faster reconstruction. The achieved reconstruction speed-up in our experiments is up to 140-175.