Generalized Dual Discriminator GANs

Dual discriminator generative adversarial networks (D2 GANs) were introduced to mitigate the problem of mode collapse in generative adversarial networks. In D2 GANs, two discriminators are employed alongside a generator: one discriminator rewards high scores for samples from the true data distribution, while the other favors samples from the generator. In this work, we first introduce dual discriminator $\alpha$-GANs (D2 $\alpha$-GANs), which combines the strengths of dual discriminators with the flexibility of a tunable loss function, $\alpha$-loss. We further generalize this approach to arbitrary functions defined on positive reals, leading to a broader class of models we refer to as generalized dual discriminator generative adversarial networks. For each of these proposed models, we provide theoretical analysis and show that the associated min-max optimization reduces to the minimization of a linear combination of an $f$-divergence and a reverse $f$-divergence. This generalizes the known simplification for D2-GANs, where the objective reduces to a linear combination of the KL-divergence and the reverse KL-divergence. Finally, we perform experiments on 2D synthetic data and use multiple performance metrics to capture various advantages of our GANs.

Addressing GAN Training Instabilities via Tunable Classification Losses

Generative adversarial networks (GANs), modeled as a zero-sum game between a generator (G) and a discriminator (D), allow generating synthetic data with formal guarantees. Noting that D is a classifier, we begin by reformulating the GAN value function using class probability estimation (CPE) losses. We prove a two-way correspondence between CPE loss GANs and $f$-GANs which minimize $f$-divergences. We also show that all symmetric $f$-divergences are equivalent in convergence. In the finite sample and model capacity setting, we define and obtain bounds on estimation and generalization errors. We specialize these results to $\alpha$-GANs, defined using $\alpha$-loss, a tunable CPE loss family parametrized by $\alpha\in(0,\infty]$. We next introduce a class of dual-objective GANs to address training instabilities of GANs by modeling each player's objective using $\alpha$-loss to obtain $(\alpha_D,\alpha_G)$-GANs. We show that the resulting non-zero sum game simplifies to minimizing an $f$-divergence under appropriate conditions on $(\alpha_D,\alpha_G)$. Generalizing this dual-objective formulation using CPE losses, we define and obtain upper bounds on an appropriately defined estimation error. Finally, we highlight the value of tuning $(\alpha_D,\alpha_G)$ in alleviating training instabilities for the synthetic 2D Gaussian mixture ring as well as the large publicly available Celeb-A and LSUN Classroom image datasets.

Towards Addressing GAN Training Instabilities: Dual-objective GANs with Tunable Parameters

In an effort to address the training instabilities of GANs, we introduce a class of dual-objective GANs with different value functions (objectives) for the generator (G) and discriminator (D). In particular, we model each objective using $\alpha$-loss, a tunable classification loss, to obtain $(\alpha_D,\alpha_G)$-GANs, parameterized by $(\alpha_D,\alpha_G)\in [0,\infty)^2$. For sufficiently large number of samples and capacities for G and D, we show that the resulting non-zero sum game simplifies to minimizing an $f$-divergence under appropriate conditions on $(\alpha_D,\alpha_G)$. In the finite sample and capacity setting, we define estimation error to quantify the gap in the generator's performance relative to the optimal setting with infinite samples and obtain upper bounds on this error, showing it to be order optimal under certain conditions. Finally, we highlight the value of tuning $(\alpha_D,\alpha_G)$ in alleviating training instabilities for the synthetic 2D Gaussian mixture ring and the Stacked MNIST datasets.

$α$-GAN: Convergence and Estimation Guarantees

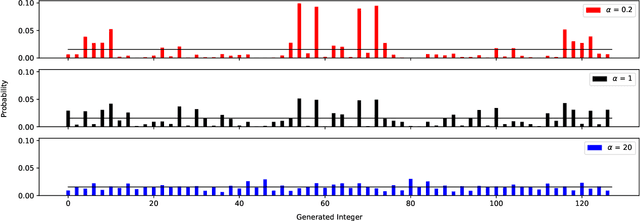
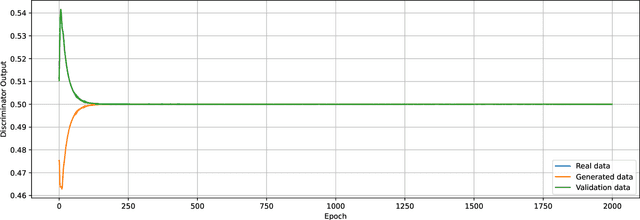
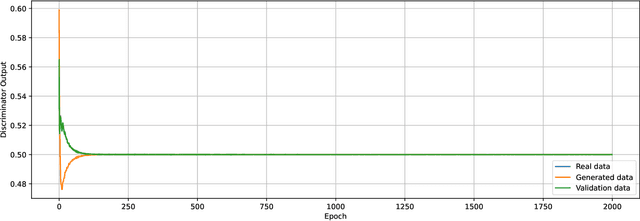
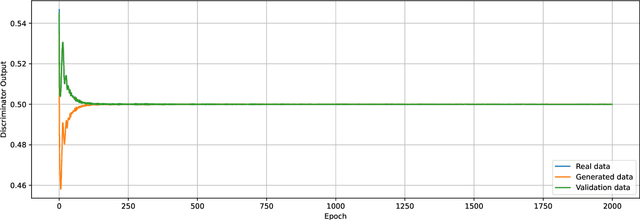
We prove a two-way correspondence between the min-max optimization of general CPE loss function GANs and the minimization of associated $f$-divergences. We then focus on $\alpha$-GAN, defined via the $\alpha$-loss, which interpolates several GANs (Hellinger, vanilla, Total Variation) and corresponds to the minimization of the Arimoto divergence. We show that the Arimoto divergences induced by $\alpha$-GAN equivalently converge, for all $\alpha\in \mathbb{R}_{>0}\cup\{\infty\}$. However, under restricted learning models and finite samples, we provide estimation bounds which indicate diverse GAN behavior as a function of $\alpha$. Finally, we present empirical results on a toy dataset that highlight the practical utility of tuning the $\alpha$ hyperparameter.

Realizing GANs via a Tunable Loss Function

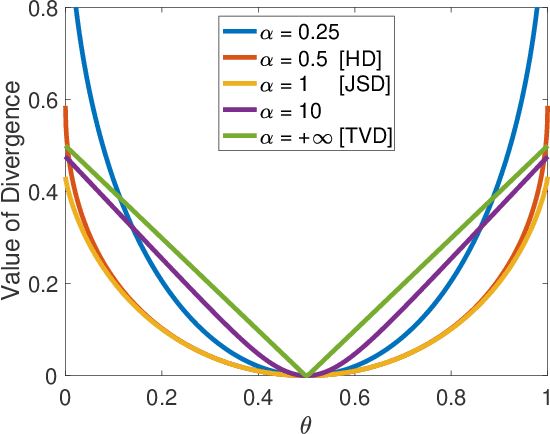
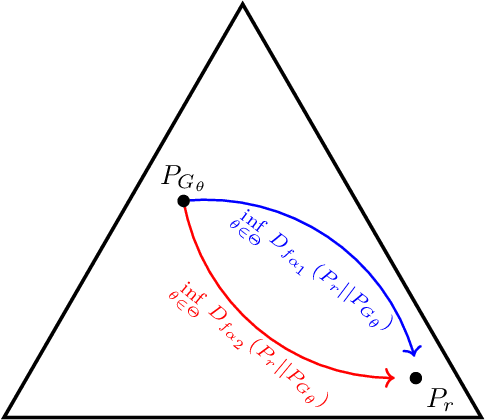
We introduce a tunable GAN, called $\alpha$-GAN, parameterized by $\alpha \in (0,\infty]$, which interpolates between various $f$-GANs and Integral Probability Metric based GANs (under constrained discriminator set). We construct $\alpha$-GAN using a supervised loss function, namely, $\alpha$-loss, which is a tunable loss function capturing several canonical losses. We show that $\alpha$-GAN is intimately related to the Arimoto divergence, which was first proposed by \"{O}sterriecher (1996), and later studied by Liese and Vajda (2006). We posit that the holistic understanding that $\alpha$-GAN introduces will have practical benefits of addressing both the issues of vanishing gradients and mode collapse.