A ZeNN architecture to avoid the Gaussian trap

We propose a new simple architecture, Zeta Neural Networks (ZeNNs), in order to overcome several shortcomings of standard multi-layer perceptrons (MLPs). Namely, in the large width limit, MLPs are non-parametric, they do not have a well-defined pointwise limit, they lose non-Gaussian attributes and become unable to perform feature learning; moreover, finite width MLPs perform poorly in learning high frequencies. The new ZeNN architecture is inspired by three simple principles from harmonic analysis: i) Enumerate the perceptons and introduce a non-learnable weight to enforce convergence; ii) Introduce a scaling (or frequency) factor; iii) Choose activation functions that lead to near orthogonal systems. We will show that these ideas allow us to fix the referred shortcomings of MLPs. In fact, in the infinite width limit, ZeNNs converge pointwise, they exhibit a rich asymptotic structure beyond Gaussianity, and perform feature learning. Moreover, when appropriate activation functions are chosen, (finite width) ZeNNs excel at learning high-frequency features of functions with low dimensional domains.

The Positivity of the Neural Tangent Kernel

The Neural Tangent Kernel (NTK) has emerged as a fundamental concept in the study of wide Neural Networks. In particular, it is known that the positivity of the NTK is directly related to the memorization capacity of sufficiently wide networks, i.e., to the possibility of reaching zero loss in training, via gradient descent. Here we will improve on previous works and obtain a sharp result concerning the positivity of the NTK of feedforward networks of any depth. More precisely, we will show that, for any non-polynomial activation function, the NTK is strictly positive definite. Our results are based on a novel characterization of polynomial functions which is of independent interest.

Wide neural networks: From non-gaussian random fields at initialization to the NTK geometry of training

Recent developments in applications of artificial neural networks with over $n=10^{14}$ parameters make it extremely important to study the large $n$ behaviour of such networks. Most works studying wide neural networks have focused on the infinite width $n \to +\infty$ limit of such networks and have shown that, at initialization, they correspond to Gaussian processes. In this work we will study their behavior for large, but finite $n$. Our main contributions are the following: (1) The computation of the corrections to Gaussianity in terms of an asymptotic series in $n^{-\frac{1}{2}}$. The coefficients in this expansion are determined by the statistics of parameter initialization and by the activation function. (2) Controlling the evolution of the outputs of finite width $n$ networks, during training, by computing deviations from the limiting infinite width case (in which the network evolves through a linear flow). This improves previous estimates and yields sharper decay rates for the (finite width) NTK in terms of $n$, valid during the entire training procedure. As a corollary, we also prove that, with arbitrarily high probability, the training of sufficiently wide neural networks converges to a global minimum of the corresponding quadratic loss function. (3) Estimating how the deviations from Gaussianity evolve with training in terms of $n$. In particular, using a certain metric in the space of measures we find that, along training, the resulting measure is within $n^{-\frac{1}{2}}(\log n)^{1+}$ of the time dependent Gaussian process corresponding to the infinite width network (which is explicitly given by precomposing the initial Gaussian process with the linear flow corresponding to training in the infinite width limit).

Automatic Graphic Logo Detection via Fast Region-based Convolutional Networks

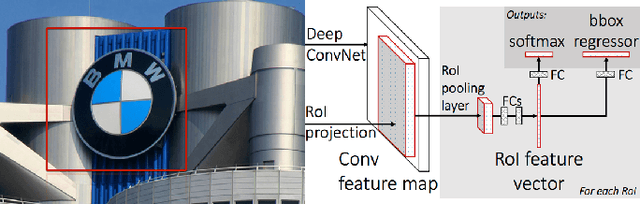
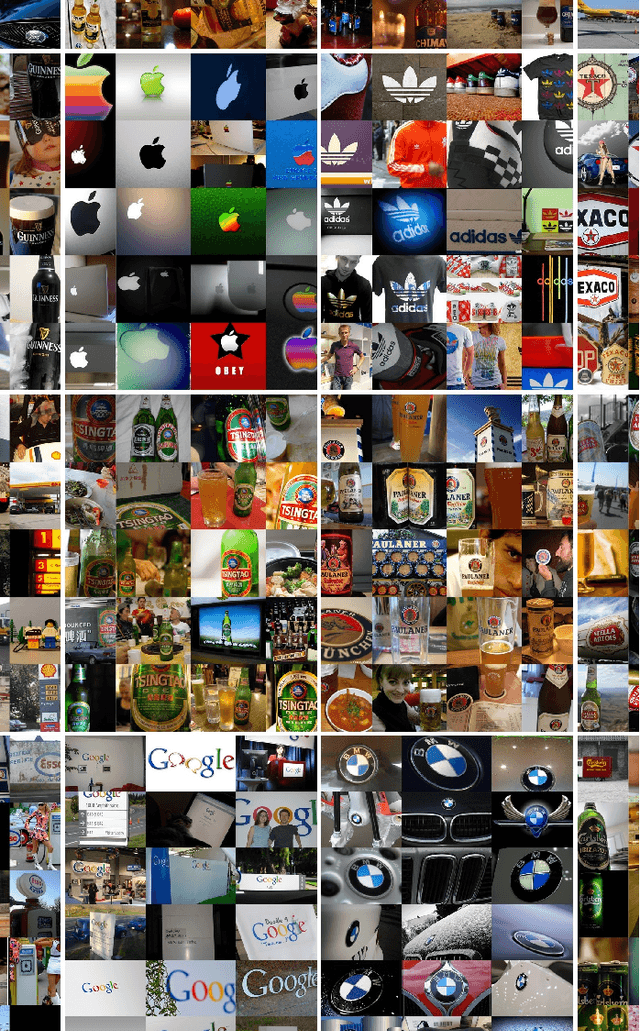
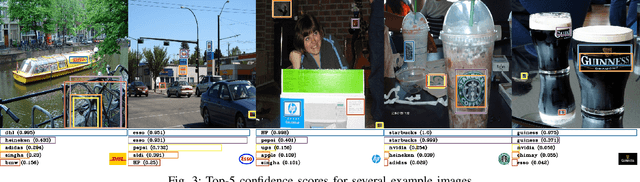
Brand recognition is a very challenging topic with many useful applications in localization recognition, advertisement and marketing. In this paper we present an automatic graphic logo detection system that robustly handles unconstrained imaging conditions. Our approach is based on Fast Region-based Convolutional Networks (FRCN) proposed by Ross Girshick, which have shown state-of-the-art performance in several generic object recognition tasks (PASCAL Visual Object Classes challenges). In particular, we use two CNN models pre-trained with the ILSVRC ImageNet dataset and we look at the selective search of windows `proposals' in the pre-processing stage and data augmentation to enhance the logo recognition rate. The novelty lies in the use of transfer learning to leverage powerful Convolutional Neural Network models trained with large-scale datasets and repurpose them in the context of graphic logo detection. Another benefit of this framework is that it allows for multiple detections of graphic logos using regions that are likely to have an object. Experimental results with the FlickrLogos-32 dataset show not only the promising performance of our developed models with respect to noise and other transformations a graphic logo can be subject to, but also its superiority over state-of-the-art systems with hand-crafted models and features.