Feedback Motion Plan Verification for Vehicles with Bounded Curvature Constraints

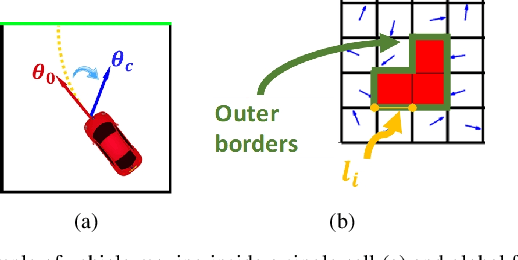
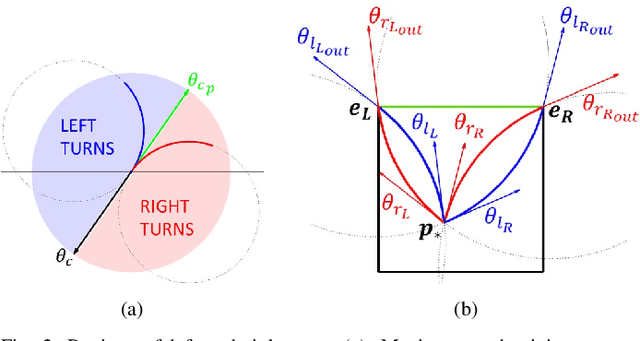
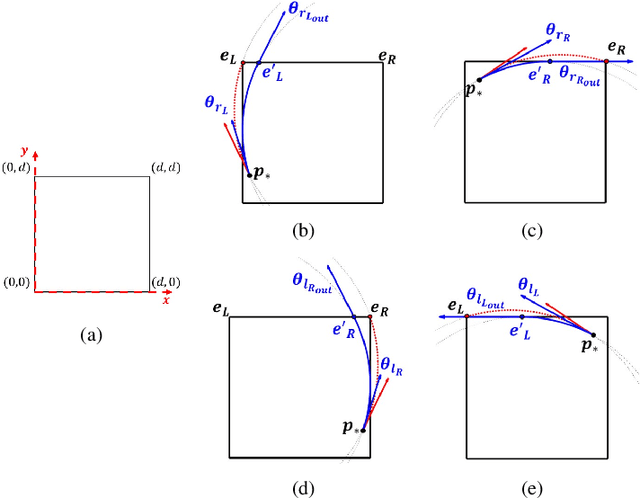
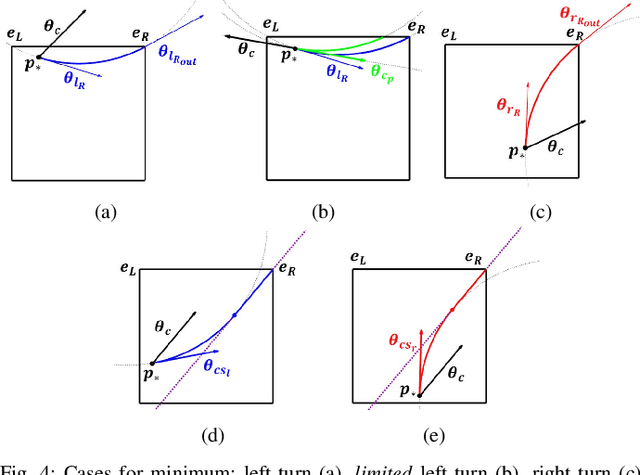
The kinematic approximation of Dubin's Vehicle has been largely exploited in the formulation of various motion planning methods. In the majority of these methods, planning and control phases are decoupled, and the burden of rejecting disturbances is left to the controller. An alternative to this approach is the use of a feedback motion plan, where for each state there is a specific pre-computed action that will be executed. This planning approach provides the ability to verify all trajectories off-line. The verification can be performed using backward reachability, which provides the set of configurations from which a region is reachable. In this paper, we formulate a verification process that relies on the computation of the backward reachable set using geometric principles. In addition to the theoretical foundation of the method, we provide a numerical implementation of the method and we illustrate a practical example.

A Feedback Motion Plan for Vehicles with Bounded Curvature Constraints

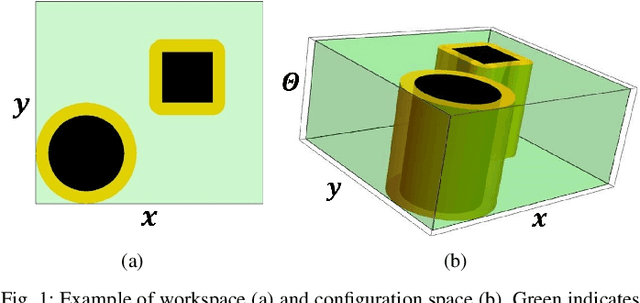
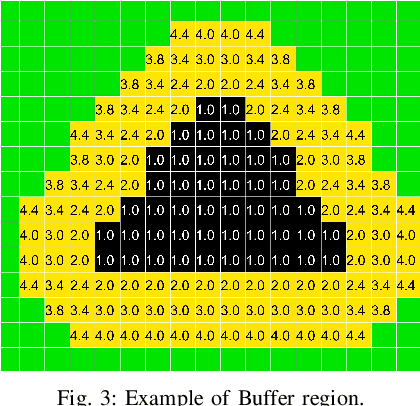
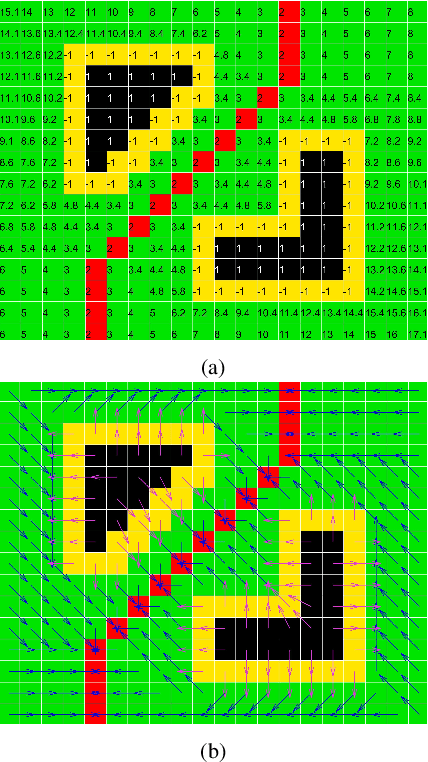
The use of a feedback motion plan instead of the decoupled scheme consisting of separate plan and control phases can facilitate the task of proving the properties of an autonomous system. The advantage of using a feedback motion plan is the possibility to validate the whole plan offline before its execution, which means that trajectories having different initial states can be tested simultaneously. In this paper, we formulate a feedback motion plan based on the extension of the \emph{wavefront expansion} to the case of vehicles having bounded curvature. Additionally, the use of a transition function and a Gaussian filter limits undesired oscillations in the resultant trajectories. The method is suitable for both single goal missions and path following. The paper illustrates the algorithm for the generation of the plan and presents simulation data containing example trajectories and analysis of tuning parameters. Finally, future developments are discussed.