Individuation of 3D perceptual units from neurogeometry of binocular cells

We model the functional architecture of the early stages of three-dimensional vision by extending the neurogeometric sub-Riemannian model for stereo-vision introduced in \cite{BCSZ23}. A new framework for correspondence is introduced that integrates a neural-based algorithm to achieve stereo correspondence locally while, simultaneously, organizing the corresponding points into global perceptual units. The result is an effective scene segmentation. We achieve this using harmonic analysis on the sub-Riemannian structure and show, in a comparison against Riemannian distance, that the sub-Riemannian metric is central to the solution.

A Neural Network Ensemble Approach to System Identification

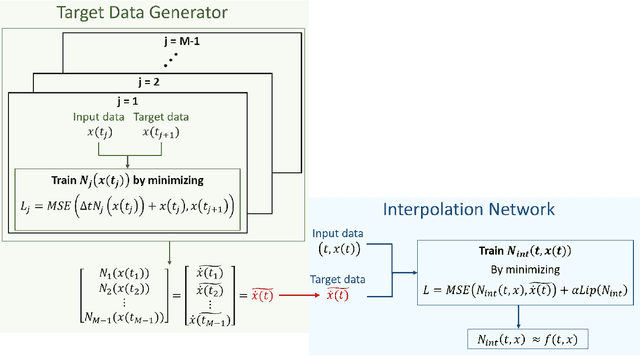
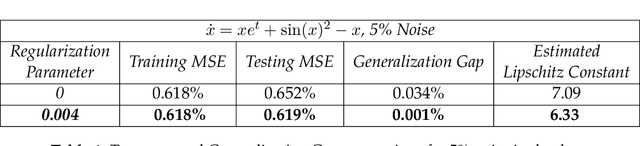
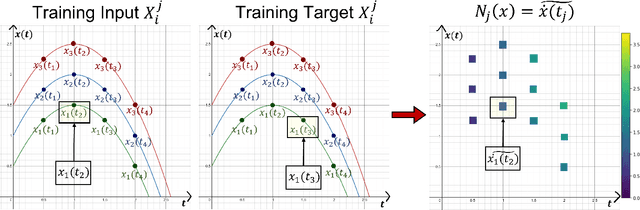
We present a new algorithm for learning unknown governing equations from trajectory data, using and ensemble of neural networks. Given samples of solutions $x(t)$ to an unknown dynamical system $\dot{x}(t)=f(t,x(t))$, we approximate the function $f$ using an ensemble of neural networks. We express the equation in integral form and use Euler method to predict the solution at every successive time step using at each iteration a different neural network as a prior for $f$. This procedure yields M-1 time-independent networks, where M is the number of time steps at which $x(t)$ is observed. Finally, we obtain a single function $f(t,x(t))$ by neural network interpolation. Unlike our earlier work, where we numerically computed the derivatives of data, and used them as target in a Lipschitz regularized neural network to approximate $f$, our new method avoids numerical differentiations, which are unstable in presence of noise. We test the new algorithm on multiple examples both with and without noise in the data. We empirically show that generalization and recovery of the governing equation improve by adding a Lipschitz regularization term in our loss function and that this method improves our previous one especially in presence of noise, when numerical differentiation provides low quality target data. Finally, we compare our results with the method proposed by Raissi, et al. arXiv:1801.01236 (2018) and with SINDy.

Emergence of Lie symmetries in functional architectures learned by CNNs

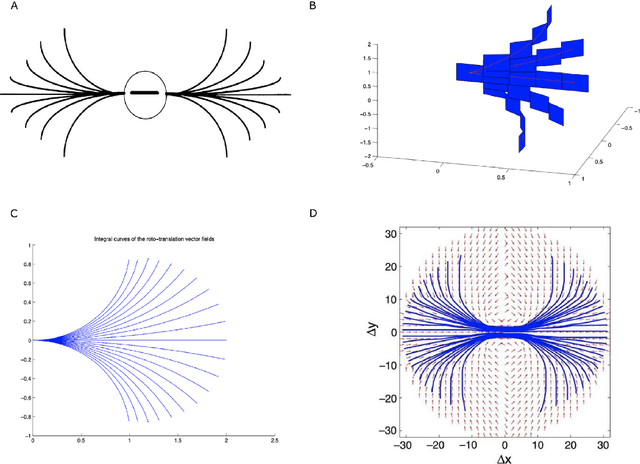
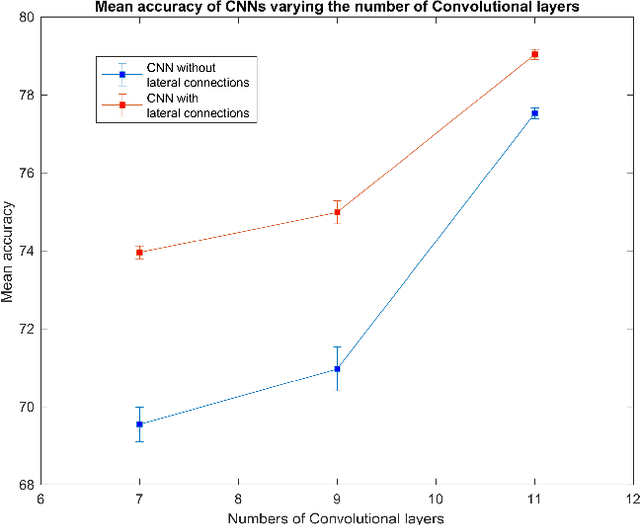
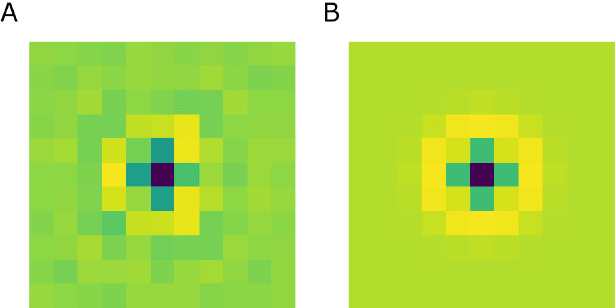
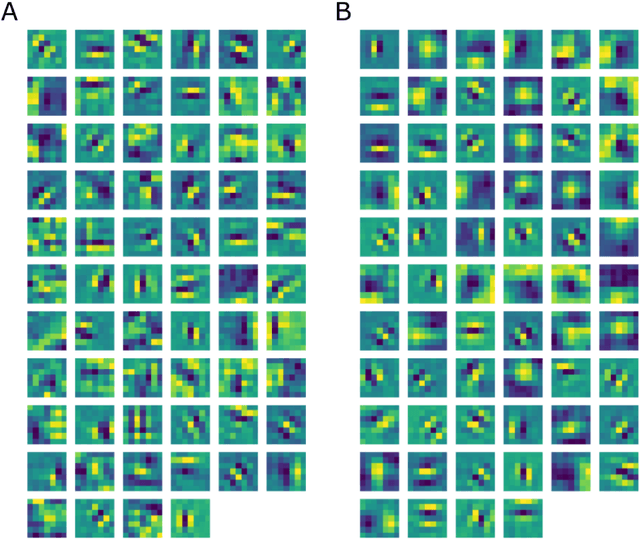
In this paper we study the spontaneous development of symmetries in the early layers of a Convolutional Neural Network (CNN) during learning on natural images. Our architecture is built in such a way to mimic the early stages of biological visual systems. In particular, it contains a pre-filtering step $\ell^0$ defined in analogy with the Lateral Geniculate Nucleus (LGN). Moreover, the first convolutional layer is equipped with lateral connections defined as a propagation driven by a learned connectivity kernel, in analogy with the horizontal connectivity of the primary visual cortex (V1). The layer $\ell^0$ shows a rotational symmetric pattern well approximated by a Laplacian of Gaussian (LoG), which is a well-known model of the receptive profiles of LGN cells. The convolutional filters in the first layer can be approximated by Gabor functions, in agreement with well-established models for the profiles of simple cells in V1. We study the learned lateral connectivity kernel of this layer, showing the emergence of orientation selectivity w.r.t. the learned filters. We also examine the association fields induced by the learned kernel, and show qualitative and quantitative comparisons with known group-based models of V1 horizontal connectivity. These geometric properties arise spontaneously during the training of the CNN architecture, analogously to the emergence of symmetries in visual systems thanks to brain plasticity driven by external stimuli.

System Identification Through Lipschitz Regularized Deep Neural Networks

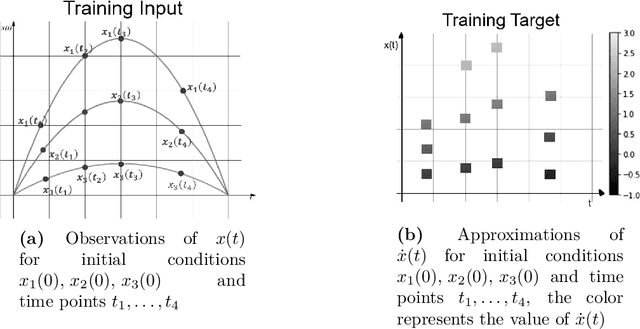
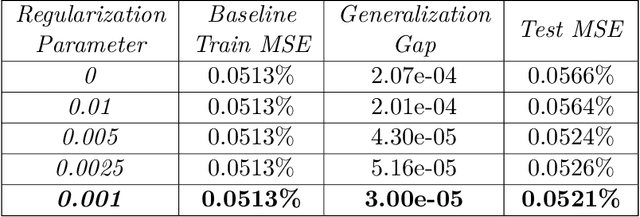
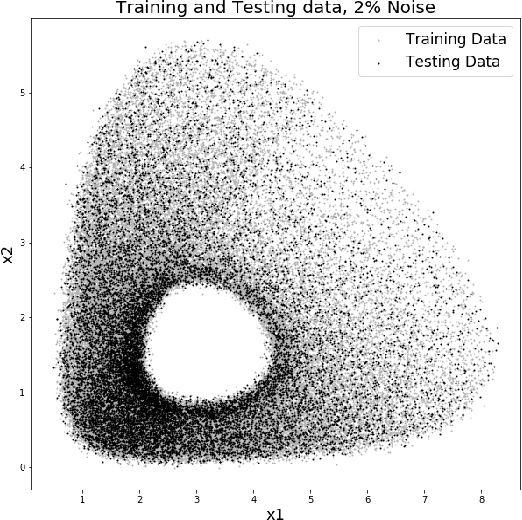
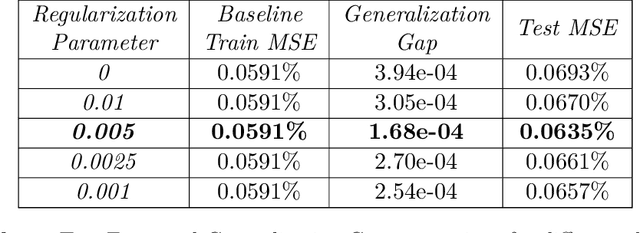
In this paper we use neural networks to learn governing equations from data. Specifically we reconstruct the right-hand side of a system of ODEs $\dot{x}(t) = f(t, x(t))$ directly from observed uniformly time-sampled data using a neural network. In contrast with other neural network based approaches to this problem, we add a Lipschitz regularization term to our loss function. In the synthetic examples we observed empirically that this regularization results in a smoother approximating function and better generalization properties when compared with non-regularized models, both on trajectory and non-trajectory data, especially in presence of noise. In contrast with sparse regression approaches, since neural networks are universal approximators, we don't need any prior knowledge on the ODE system. Since the model is applied component wise, it can handle systems of any dimension, making it usable for real-world data.

LGN-CNN: a biologically inspired CNN architecture

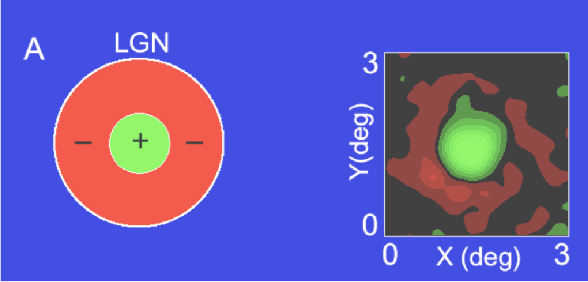
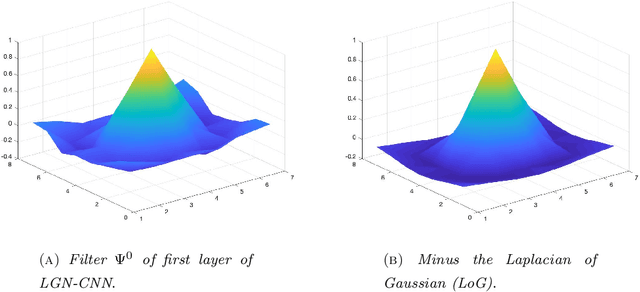
In this paper we introduce a biologically inspired CNN architecture that has a first convolutional layer that mimics the role of the LGN. The first layer of the net shows a rotationally symmetric pattern justified by the structure of the net itself that turns up to be an approximation of a Laplacian of Gaussian. The latter function is in turn a good approximation of the receptive profiles of the cells in the LGN. The analogy with respect to the visual system structure is established, emerging directly from the architecture of the net.

KerCNNs: biologically inspired lateral connections for classification of corrupted images

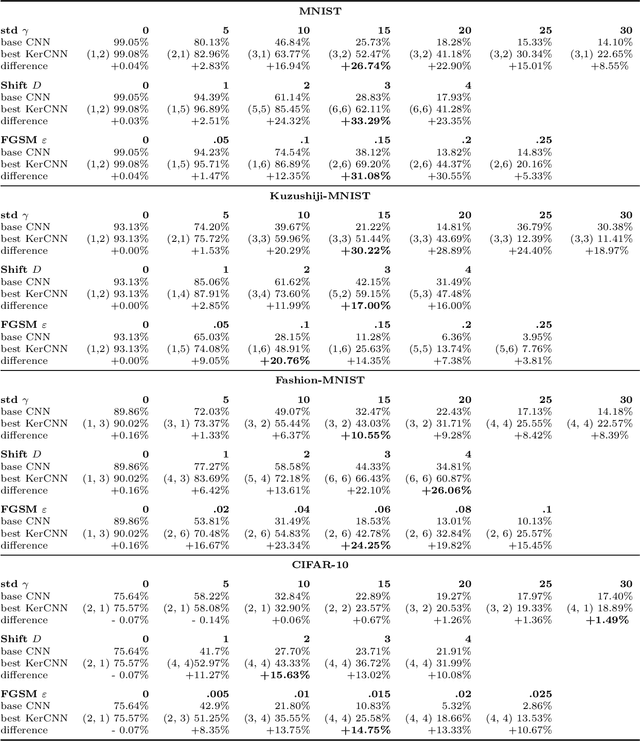
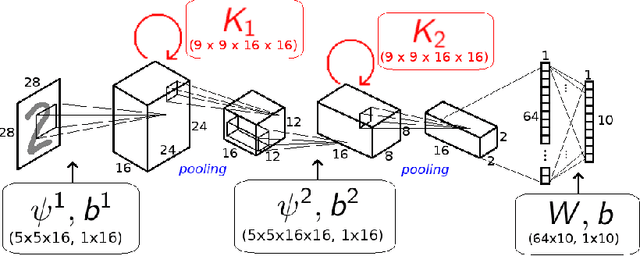
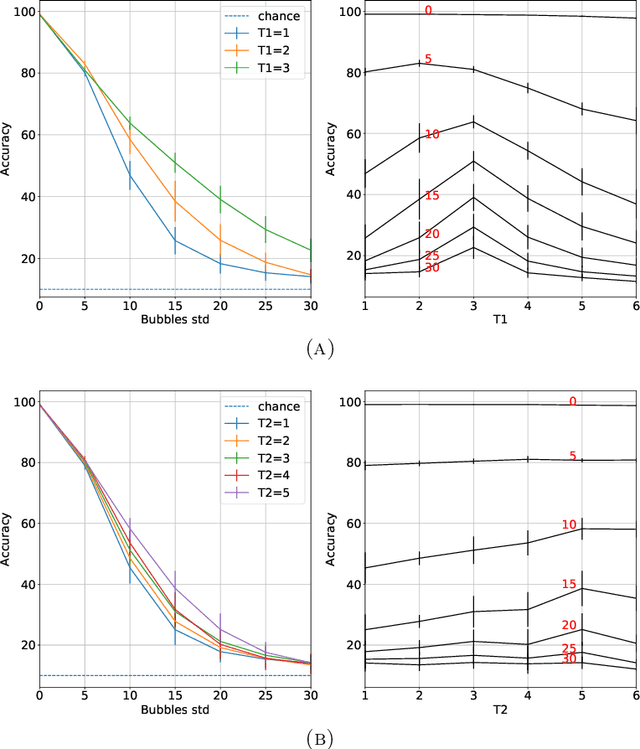
The state of the art in many computer vision tasks is represented by Convolutional Neural Networks (CNNs). Although their hierarchical organization and local feature extraction are inspired by the structure of primate visual systems, the lack of lateral connections in such architectures critically distinguishes their analysis from biological object processing. The idea of enriching CNNs with recurrent lateral connections of convolutional type has been put into practice in recent years, in the form of learned recurrent kernels with no geometrical constraints. In the present work, we introduce biologically plausible lateral kernels encoding a notion of correlation between the feedforward filters of a CNN: at each layer, the associated kernel acts as a transition kernel on the space of activations. The lateral kernels are defined in terms of the filters, thus providing a parameter-free approach to assess the geometry of horizontal connections based on the feedforward structure. We then test this new architecture, which we call KerCNN, on a generalization task related to global shape analysis and pattern completion: once trained for performing basic image classification, the network is evaluated on corrupted testing images. The image perturbations examined are designed to undermine the recognition of the images via local features, thus requiring an integration of context information - which in biological vision is critically linked to lateral connectivity. Our KerCNNs turn out to be far more stable than CNNs and recurrent CNNs to such degradations, thus validating this biologically inspired approach to reinforce object recognition under challenging conditions.

Neurogeometry of perception: isotropic and anisotropic aspects

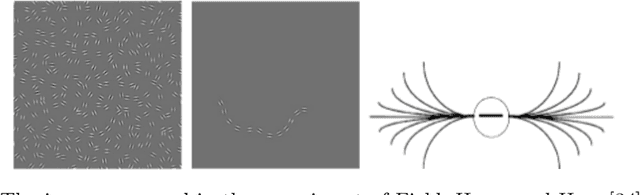
In this paper we first recall the definition of geometical model of the visual cortex, focusing in particular on the geometrical properties of horizontal cortical connectivity. Then we recognize that histograms of edges - co-occurrences are not isotropic distributed, and are strongly biased in horizontal and vertical directions of the stimulus. Finally we introduce a new model of non isotropic cortical connectivity modeled on the histogram of edges - co-occurrences. Using this kernel we are able to justify oblique phenomena comparable with experimental findings.

Curvature Integration in a 5D Kernel for Extracting Vessel Connections in Retinal Images

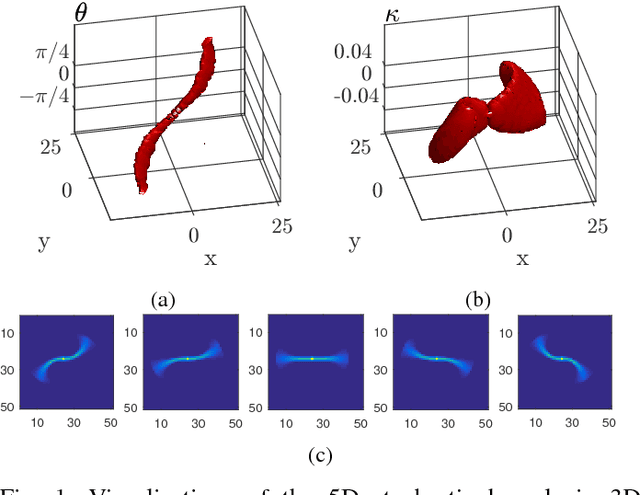
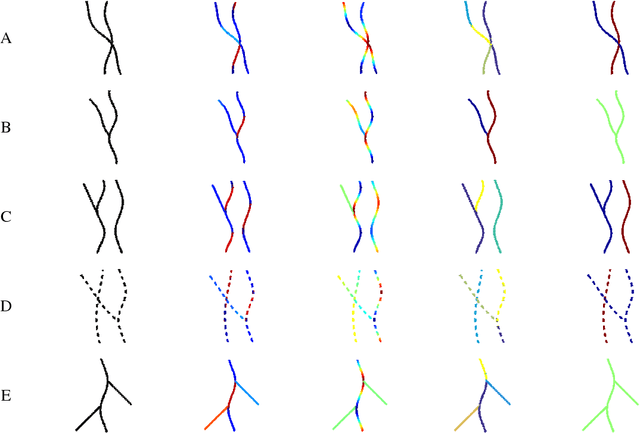
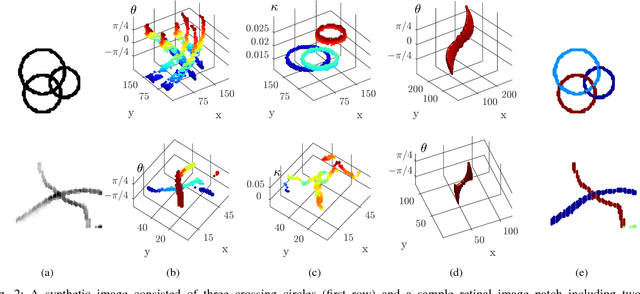
Tree-like structures such as retinal images are widely studied in computer-aided diagnosis systems for large-scale screening programs. Despite several segmentation and tracking methods proposed in the literature, there still exist several limitations specifically when two or more curvilinear structures cross or bifurcate, or in the presence of interrupted lines or highly curved blood vessels. In this paper, we propose a novel approach based on multi-orientation scores augmented with a contextual affinity matrix, which both are inspired by the geometry of the primary visual cortex (V1) and their contextual connections. The connectivity is described with a five-dimensional kernel obtained as the fundamental solution of the Fokker-Planck equation modelling the cortical connectivity in the lifted space of positions, orientations, curvatures and intensity. It is further used in a self-tuning spectral clustering step to identify the main perceptual units in the stimuli. The proposed method has been validated on several easy and challenging structures in a set of artificial images and actual retinal patches. Supported by quantitative and qualitative results, the method is capable of overcoming the limitations of current state-of-the-art techniques.

Local and global gestalt laws: A neurally based spectral approach

A mathematical model of figure-ground articulation is presented, taking into account both local and global gestalt laws. The model is compatible with the functional architecture of the primary visual cortex (V1). Particularly the local gestalt law of good continuity is described by means of suitable connectivity kernels, that are derived from Lie group theory and are neurally implemented in long range connectivity in V1. Different kernels are compatible with the geometric structure of cortical connectivity and they are derived as the fundamental solutions of the Fokker Planck, the Sub-Riemannian Laplacian and the isotropic Laplacian equations. The kernels are used to construct matrices of connectivity among the features present in a visual stimulus. Global gestalt constraints are then introduced in terms of spectral analysis of the connectivity matrix, showing that this processing can be cortically implemented in V1 by mean field neural equations. This analysis performs grouping of local features and individuates perceptual units with the highest saliency. Numerical simulations are performed and results are obtained applying the technique to a number of stimuli.

Cortical spatio-temporal dimensionality reduction for visual grouping

The visual systems of many mammals, including humans, is able to integrate the geometric information of visual stimuli and to perform cognitive tasks already at the first stages of the cortical processing. This is thought to be the result of a combination of mechanisms, which include feature extraction at single cell level and geometric processing by means of cells connectivity. We present a geometric model of such connectivities in the space of detected features associated to spatio-temporal visual stimuli, and show how they can be used to obtain low-level object segmentation. The main idea is that of defining a spectral clustering procedure with anisotropic affinities over datasets consisting of embeddings of the visual stimuli into higher dimensional spaces. Neural plausibility of the proposed arguments will be discussed.