Efficient Approximate Temporal Triangle Counting in Streaming with Predictions

Triangle counting is a fundamental and widely studied problem on static graphs, and recently on temporal graphs, where edges carry information on the timings of the associated events. Streaming processing and resource efficiency are crucial requirements for counting triangles in modern massive temporal graphs, with millions of nodes and up to billions of temporal edges. However, current exact and approximate algorithms are unable to handle large-scale temporal graphs. To fill such a gap, we introduce STEP, a scalable and efficient algorithm to approximate temporal triangle counts from a stream of temporal edges. STEP combines predictions to the number of triangles a temporal edge is involved in, with a simple sampling strategy, leading to scalability, efficiency, and accurate approximation of all eight temporal triangle types simultaneously. We analytically prove that, by using a sublinear amount of memory, STEP obtains unbiased and very accurate estimates. In fact, even noisy predictions can significantly reduce the variance of STEP's estimates. Our extensive experiments on massive temporal graphs with up to billions of edges demonstrate that STEP outputs high-quality estimates and is more efficient than state-of-the-art methods.

Gated recurrent units and temporal convolutional network for multilabel classification

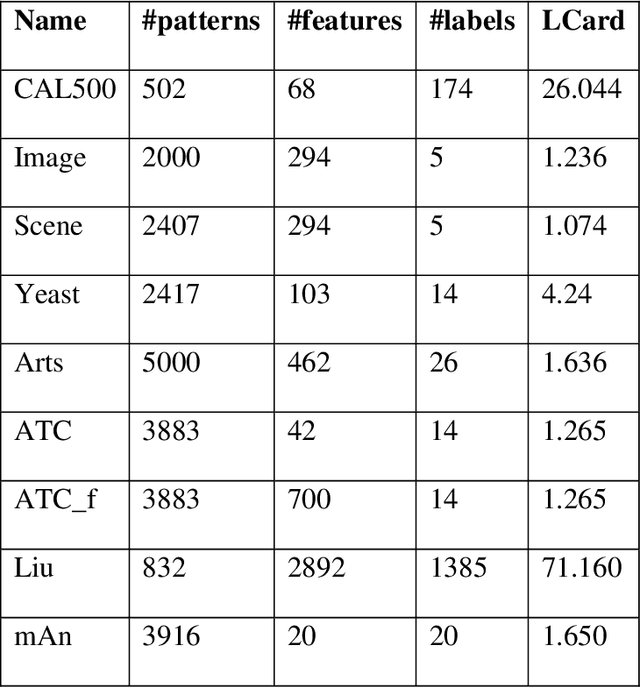
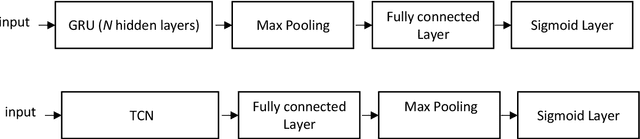
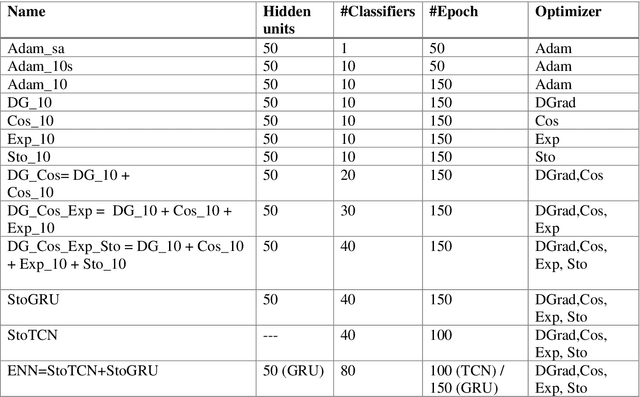
Multilabel learning tackles the problem of associating a sample with multiple class labels. This work proposes a new ensemble method for managing multilabel classification: the core of the proposed approach combines a set of gated recurrent units and temporal convolutional neural networks trained with variants of the Adam optimization approach. Multiple Adam variants, including novel one proposed here, are compared and tested; these variants are based on the difference between present and past gradients, with step size adjusted for each parameter. The proposed neural network approach is also combined with Incorporating Multiple Clustering Centers (IMCC), which further boosts classification performance. Multiple experiments on nine data sets representing a wide variety of multilabel tasks demonstrate the robustness of our best ensemble, which is shown to outperform the state-of-the-art. The MATLAB code for generating the best ensembles in the experimental section will be available at https://github.com/LorisNanni.