Inductive Position Sensors based on Coupling of Coils on Printed Circuit Boards for Demanding Automotive Applications

Rotor position feedback is required in many industrial and automotive applications, e.g. for field-oriented control of brushless motors. Traditionally, magnetic sensors, resolvers or optical encoders are used to measure the rotor position. However, advances in inductive sensing concepts enable a low-cost, high-precision position measurement principle which is robust against magnetic stray fields exceeding 4000 A/m. The operating principle is based on the coupling of a transmitter coil with several receiver coils in the megahertz frequency range. The coils are part of a printed circuit board (PCB) which also comprises circuitry for demodulation and signal processing. The transmitter coil induces eddy currents in an electrically conductive passive coupling element, which provides position-dependent amplitude modulation. The voltage induced in the receiver coils encodes the rotor angle information, typically in quadrature signals. The coupling element requires no rare-earth materials and can be made of stainless steel, for instance. The PCB-based design of the sensor offers considerable flexibility in optimizing its performance. By tailoring the coil geometry and arrangement, accuracy, air gap and overall sensor dimensions can be adjusted to meet a broad range of application-specific requirements. A sensor design sample exhibits a mechanical angle error less than 0.02{\deg} (0.1{\deg} electrical) in both, finite-element simulation and test bench measurement, with good agreement.

Harmonic analysis of the arctangent function regarding the angular error introduced by superimposed Fourier series for application in sine/cosine angle encoders

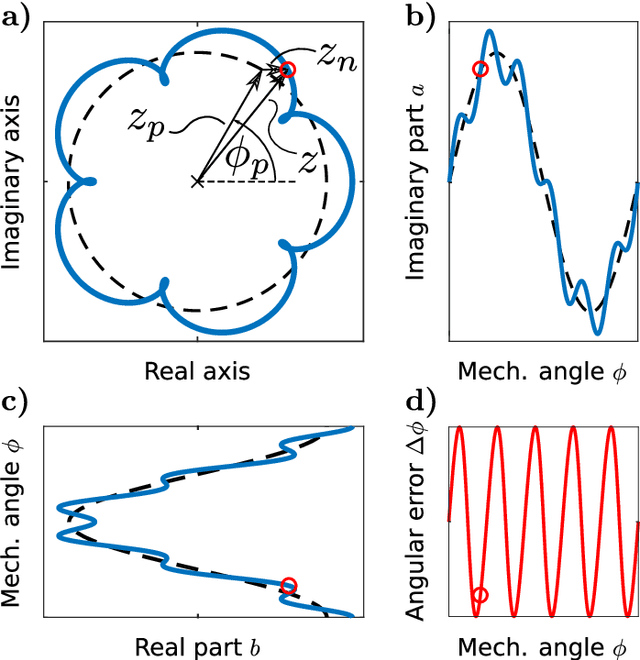
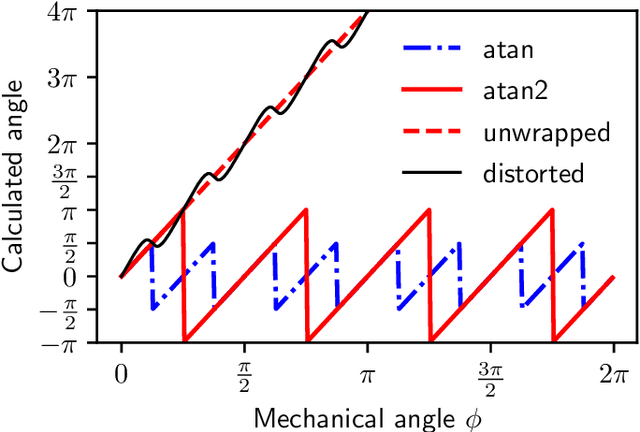
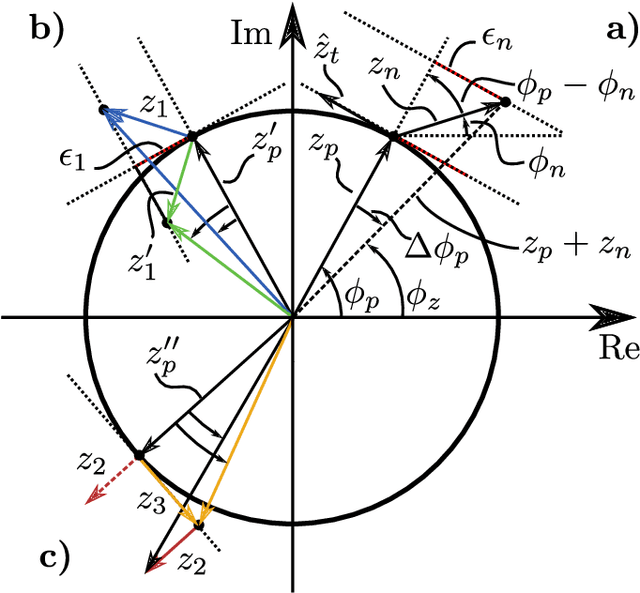
We present a rigorous analytical method for harmonic analysis of the angular error of rotary and linear encoders with sine/cosine output signals in quadrature that are distorted by superimposed Fourier series. To calculate the angle from measured sine and cosine encoder channels in quadrature, the arctangent function is commonly used. The hence non-linear relation between raw signals and calculated angle -- often thought of as a black box -- complicates the estimation of the angular error and its harmonic decomposition. By means of a Taylor series expansion of the harmonic amplitudes, our method allows for quantification of the impact of harmonic signal distortions on the angular error in terms of harmonic order, magnitude and phase, including an upper bound on the remaining error term -- without numerical evaluation of the arctangent function. The same approximation is achieved with an intuitive geometric approximation in the complex plane, validating the results. Additionally, interaction effects between harmonics in the signals are considered by higher-order Taylor expansion. The approximations show an excellent agreement with the exact calculation in numerical examples even in case of large distortion amplitudes, leading to practicable estimates for the angular error decomposition.