Compositionality Unlocks Deep Interpretable Models

We propose $\chi$-net, an intrinsically interpretable architecture combining the compositional multilinear structure of tensor networks with the expressivity and efficiency of deep neural networks. $\chi$-nets retain equal accuracy compared to their baseline counterparts. Our novel, efficient diagonalisation algorithm, ODT, reveals linear low-rank structure in a multilayer SVHN model. We leverage this toward formal weight-based interpretability and model compression.

Quantum Methods for Managing Ambiguity in Natural Language Processing

The Categorical Compositional Distributional (DisCoCat) framework models meaning in natural language using the mathematical framework of quantum theory, expressed as formal diagrams. DisCoCat diagrams can be associated with tensor networks and quantum circuits. DisCoCat diagrams have been connected to density matrices in various contexts in Quantum Natural Language Processing (QNLP). Previous use of density matrices in QNLP entails modelling ambiguous words as probability distributions over more basic words (the word \texttt{queen}, e.g., might mean the reigning queen or the chess piece). In this article, we investigate using probability distributions over processes to account for syntactic ambiguity in sentences. The meanings of these sentences are represented by density matrices. We show how to create probability distributions on quantum circuits that represent the meanings of sentences and explain how this approach generalises tasks from the literature. We conduct an experiment to validate the proposed theory.

Yin-Yang: Developing Motifs With Long-Term Structure And Controllability

Transformer models have made great strides in generating symbolically represented music with local coherence. However, controlling the development of motifs in a structured way with global form remains an open research area. One of the reasons for this challenge is due to the note-by-note autoregressive generation of such models, which lack the ability to correct themselves after deviations from the motif. In addition, their structural performance on datasets with shorter durations has not been studied in the literature. In this study, we propose Yin-Yang, a framework consisting of a phrase generator, phrase refiner, and phrase selector models for the development of motifs into melodies with long-term structure and controllability. The phrase refiner is trained on a novel corruption-refinement strategy which allows it to produce melodic and rhythmic variations of an original motif at generation time, thereby rectifying deviations of the phrase generator. We also introduce a new objective evaluation metric for quantifying how smoothly the motif manifests itself within the piece. Evaluation results show that our model achieves better performance compared to state-of-the-art transformer models while having the advantage of being controllable and making the generated musical structure semi-interpretable, paving the way for musical analysis. Our code and demo page can be found at https://github.com/keshavbhandari/yinyang.

A New Corpus for Computational Music Research and A Novel Method for Musical Structure Analysis

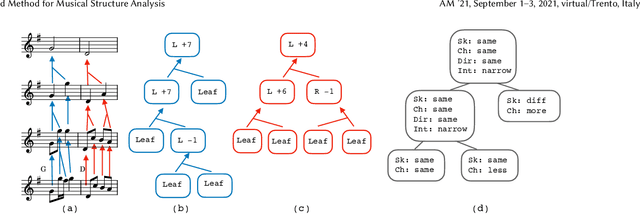
Computational models of music, while providing good descriptions of melodic development, still cannot fully grasp the general structure comprised of repetitions, transpositions, and reuse of melodic material. We present a corpus of strongly structured baroque allemandes, and describe a top-down approach to abstract the shared structure of their musical content using tree representations produced from pairwise differences between the Schenkerian-inspired analyses of each piece, thereby providing a rich hierarchical description of the corpus.