Noisy Interpolation Learning with Shallow Univariate ReLU Networks

We study the asymptotic overfitting behavior of interpolation with minimum norm ($\ell_2$ of the weights) two-layer ReLU networks for noisy univariate regression. We show that overfitting is tempered for the $L_1$ loss, and any $L_p$ loss for $p<2$, but catastrophic for $p\geq 2$.

Deconstructing Data Reconstruction: Multiclass, Weight Decay and General Losses

Memorization of training data is an active research area, yet our understanding of the inner workings of neural networks is still in its infancy. Recently, Haim et al. (2022) proposed a scheme to reconstruct training samples from multilayer perceptron binary classifiers, effectively demonstrating that a large portion of training samples are encoded in the parameters of such networks. In this work, we extend their findings in several directions, including reconstruction from multiclass and convolutional neural networks. We derive a more general reconstruction scheme which is applicable to a wider range of loss functions such as regression losses. Moreover, we study the various factors that contribute to networks' susceptibility to such reconstruction schemes. Intriguingly, we observe that using weight decay during training increases reconstructability both in terms of quantity and quality. Additionally, we examine the influence of the number of neurons relative to the number of training samples on the reconstructability.

An Agnostic View on the Cost of Overfitting in Ridge Regression

We study the cost of overfitting in noisy kernel ridge regression (KRR), which we define as the ratio between the test error of the interpolating ridgeless model and the test error of the optimally-tuned model. We take an "agnostic" view in the following sense: we consider the cost as a function of sample size for any target function, even if the sample size is not large enough for consistency or the target is outside the RKHS. We analyze the cost of overfitting under a Gaussian universality ansatz using recently derived (non-rigorous) risk estimates in terms of the task eigenstructure. Our analysis provides a more refined characterization of benign, tempered and catastrophic overfitting (qv Mallinar et al. 2022).

Most Neural Networks Are Almost Learnable

We present a PTAS for learning random constant-depth networks. We show that for any fixed $\epsilon>0$ and depth $i$, there is a poly-time algorithm that for any distribution on $\sqrt{d} \cdot \mathbb{S}^{d-1}$ learns random Xavier networks of depth $i$, up to an additive error of $\epsilon$. The algorithm runs in time and sample complexity of $(\bar{d})^{\mathrm{poly}(\epsilon^{-1})}$, where $\bar d$ is the size of the network. For some cases of sigmoid and ReLU-like activations the bound can be improved to $(\bar{d})^{\mathrm{polylog}(\epsilon^{-1})}$, resulting in a quasi-poly-time algorithm for learning constant depth random networks.

Reconstructing Training Data from Multiclass Neural Networks

Reconstructing samples from the training set of trained neural networks is a major privacy concern. Haim et al. (2022) recently showed that it is possible to reconstruct training samples from neural network binary classifiers, based on theoretical results about the implicit bias of gradient methods. In this work, we present several improvements and new insights over this previous work. As our main improvement, we show that training-data reconstruction is possible in the multi-class setting and that the reconstruction quality is even higher than in the case of binary classification. Moreover, we show that using weight-decay during training increases the vulnerability to sample reconstruction. Finally, while in the previous work the training set was of size at most $1000$ from $10$ classes, we show preliminary evidence of the ability to reconstruct from a model trained on $5000$ samples from $100$ classes.

The Double-Edged Sword of Implicit Bias: Generalization vs. Robustness in ReLU Networks

In this work, we study the implications of the implicit bias of gradient flow on generalization and adversarial robustness in ReLU networks. We focus on a setting where the data consists of clusters and the correlations between cluster means are small, and show that in two-layer ReLU networks gradient flow is biased towards solutions that generalize well, but are highly vulnerable to adversarial examples. Our results hold even in cases where the network has many more parameters than training examples. Despite the potential for harmful overfitting in such overparameterized settings, we prove that the implicit bias of gradient flow prevents it. However, the implicit bias also leads to non-robust solutions (susceptible to small adversarial $\ell_2$-perturbations), even though robust networks that fit the data exist.

Benign Overfitting in Linear Classifiers and Leaky ReLU Networks from KKT Conditions for Margin Maximization

Linear classifiers and leaky ReLU networks trained by gradient flow on the logistic loss have an implicit bias towards solutions which satisfy the Karush--Kuhn--Tucker (KKT) conditions for margin maximization. In this work we establish a number of settings where the satisfaction of these KKT conditions implies benign overfitting in linear classifiers and in two-layer leaky ReLU networks: the estimators interpolate noisy training data and simultaneously generalize well to test data. The settings include variants of the noisy class-conditional Gaussians considered in previous work as well as new distributional settings where benign overfitting has not been previously observed. The key ingredient to our proof is the observation that when the training data is nearly-orthogonal, both linear classifiers and leaky ReLU networks satisfying the KKT conditions for their respective margin maximization problems behave like a nearly uniform average of the training examples.

Adversarial Examples Exist in Two-Layer ReLU Networks for Low Dimensional Data Manifolds

Despite a great deal of research, it is still not well-understood why trained neural networks are highly vulnerable to adversarial examples. In this work we focus on two-layer neural networks trained using data which lie on a low dimensional linear subspace. We show that standard gradient methods lead to non-robust neural networks, namely, networks which have large gradients in directions orthogonal to the data subspace, and are susceptible to small adversarial $L_2$-perturbations in these directions. Moreover, we show that decreasing the initialization scale of the training algorithm, or adding $L_2$ regularization, can make the trained network more robust to adversarial perturbations orthogonal to the data.

Efficiently Learning Neural Networks: What Assumptions May Suffice?

Understanding when neural networks can be learned efficiently is a fundamental question in learning theory. Existing hardness results suggest that assumptions on both the input distribution and the network's weights are necessary for obtaining efficient algorithms. Moreover, it was previously shown that depth-$2$ networks can be efficiently learned under the assumptions that the input distribution is Gaussian, and the weight matrix is non-degenerate. In this work, we study whether such assumptions may suffice for learning deeper networks and prove negative results. We show that learning depth-$3$ ReLU networks under the Gaussian input distribution is hard even in the smoothed-analysis framework, where a random noise is added to the network's parameters. It implies that learning depth-$3$ ReLU networks under the Gaussian distribution is hard even if the weight matrices are non-degenerate. Moreover, we consider depth-$2$ networks, and show hardness of learning in the smoothed-analysis framework, where both the network parameters and the input distribution are smoothed. Our hardness results are under a well-studied assumption on the existence of local pseudorandom generators.

Implicit Bias in Leaky ReLU Networks Trained on High-Dimensional Data

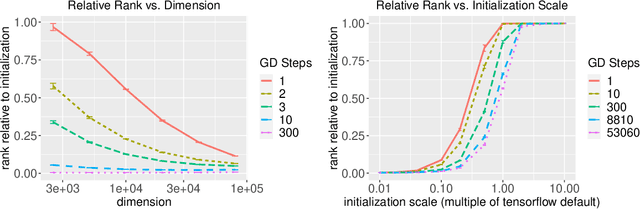
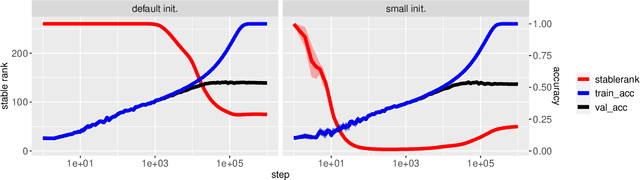
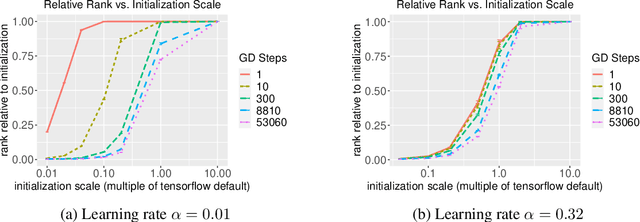
The implicit biases of gradient-based optimization algorithms are conjectured to be a major factor in the success of modern deep learning. In this work, we investigate the implicit bias of gradient flow and gradient descent in two-layer fully-connected neural networks with leaky ReLU activations when the training data are nearly-orthogonal, a common property of high-dimensional data. For gradient flow, we leverage recent work on the implicit bias for homogeneous neural networks to show that asymptotically, gradient flow produces a neural network with rank at most two. Moreover, this network is an $\ell_2$-max-margin solution (in parameter space), and has a linear decision boundary that corresponds to an approximate-max-margin linear predictor. For gradient descent, provided the random initialization variance is small enough, we show that a single step of gradient descent suffices to drastically reduce the rank of the network, and that the rank remains small throughout training. We provide experiments which suggest that a small initialization scale is important for finding low-rank neural networks with gradient descent.