Transport in reservoir computing

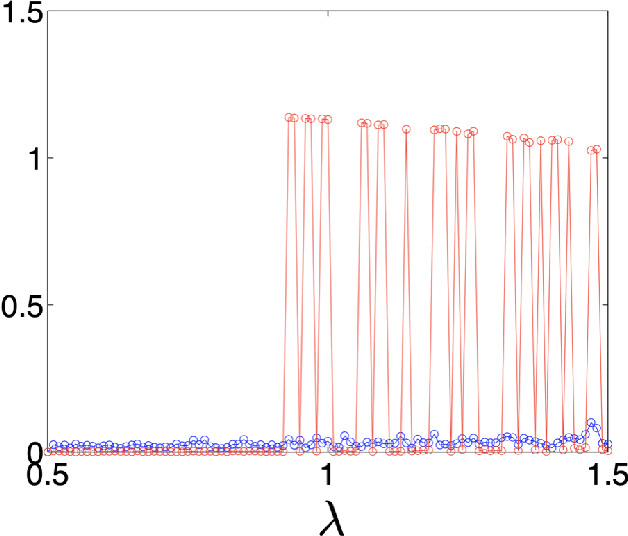
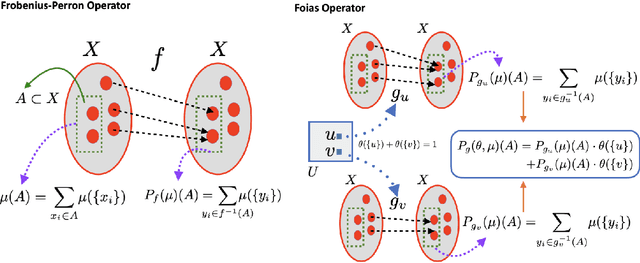
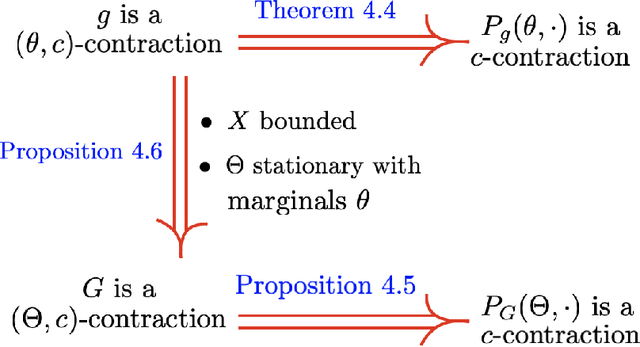
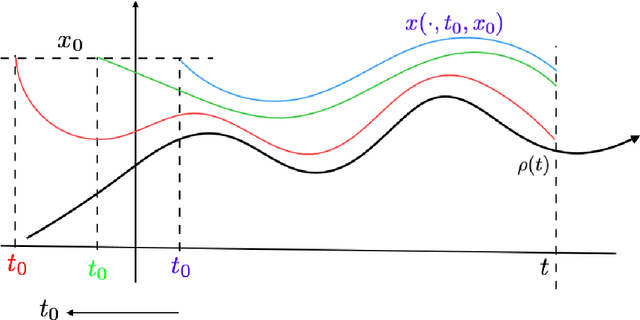
Reservoir computing systems are constructed using a driven dynamical system in which external inputs can alter the evolving states of a system. These paradigms are used in information processing, machine learning, and computation. A fundamental question that needs to be addressed in this framework is the statistical relationship between the input and the system states. This paper provides conditions that guarantee the existence and uniqueness of asymptotically invariant measures for driven systems and shows that their dependence on the input process is continuous when the set of input and output processes are endowed with the Wasserstein distance. The main tool in these developments is the characterization of those invariant measures as fixed points of naturally defined Foias operators that appear in this context and which have been profusely studied in the paper. Those fixed points are obtained by imposing a newly introduced stochastic state contractivity on the driven system that is readily verifiable in examples. Stochastic state contractivity can be satisfied by systems that are not state-contractive, which is a need typically evoked to guarantee the echo state property in reservoir computing. As a result, it may actually be satisfied even if the echo state property is not present.

Embedding Information onto a Dynamical System

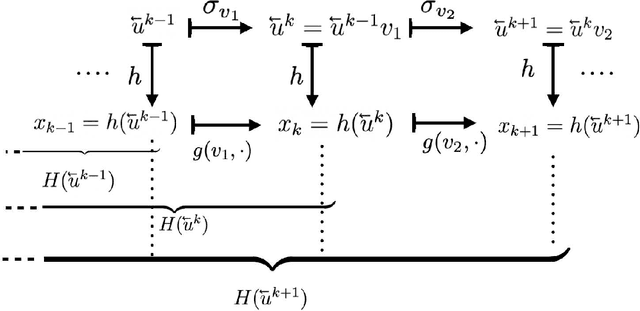
The celebrated Takens' embedding theorem concerns embedding an attractor of a dynamical system in a Euclidean space of appropriate dimension through a generic delay-observation map. The embedding also establishes a topological conjugacy. In this paper, we show how an arbitrary sequence can be mapped into another space as an attractive solution of a nonautonomous dynamical system. Such mapping also entails a topological conjugacy and an embedding between the sequence and the attractive solution spaces. This result is not a generalization of Takens embedding theorem but helps us understand what exactly is required by discrete-time state space models widely used in applications to embed an external stimulus onto its solution space. Our results settle another basic problem concerning the perturbation of an autonomous dynamical system. We describe what exactly happens to the dynamics when exogenous noise perturbs continuously a local irreducible attracting set (such as a stable fixed point) of a discrete-time autonomous dynamical system.

Universal set of Observables for the Koopman Operator through Causal Embedding

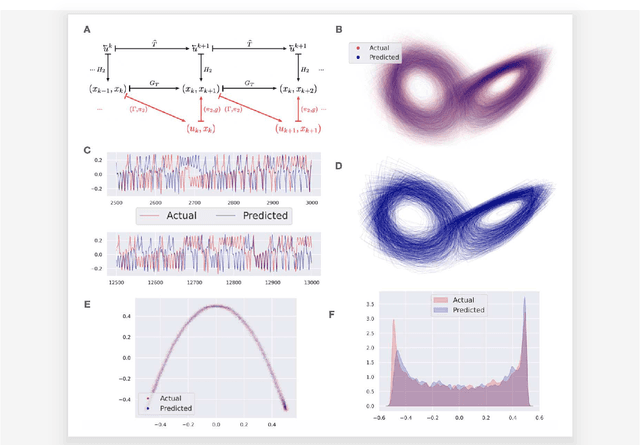
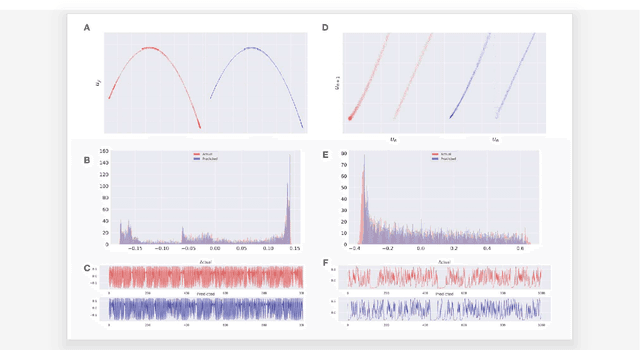
Obtaining repeated measurements from physical and natural systems for building a more informative dynamical model of such systems is engraved in modern science. Results in reconstructing equivalent chaotic dynamical systems through delay coordinate mappings, Koopman operator based data-driven approach and reservoir computing methods have shown the possibility of finding model equations on a new phase space that is relatable to the dynamical system generating the data. Recently, rigorous results that point to reducing the functional complexity of the map that describes the dynamics in the new phase have made the Koopman operator based approach very attractive for data-driven modeling. However, choosing a set of nonlinear observable functions that can work for different data sets is an open challenge. We use driven dynamical systems comparable to that in reservoir computing with the \emph{causal embedding property} to obtain the right set of observables through which the dynamics in the new space is made equivalent or topologically conjugate to the original system. Deep learning methods are used to learn a map that emerges as a consequence of the topological conjugacy. Besides stability, amenability for hardware implementations, causal embedding based models provide long-term consistency even for maps that have failed under previously reported data-driven or machine learning methods.

Memory-Loss is Fundamental for Stability and Distinguishes the Echo State Property Threshold in Reservoir Computing & Beyond

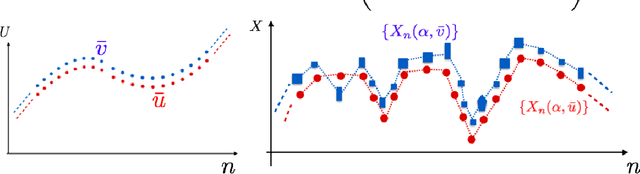
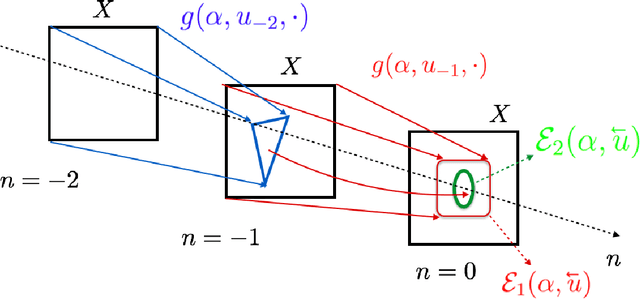
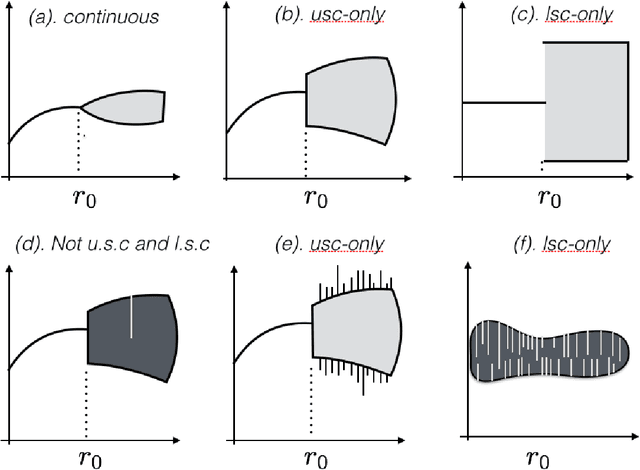
Reservoir computing, a highly successful neuromorphic computing scheme used to filter, predict, classify temporal inputs, has entered an era of microchips for several other engineering and biological applications. A basis for reservoir computing is memory-loss or the echo state property. It is an open problem on how design parameters of the reservoir can be optimized to maximize reservoir freedom to map an input robustly and yet have its close-by-variants represented in the reservoir differently. We present a framework to analyze stability due to input and parameter perturbations and make a surprising fundamental conclusion, that the echo state property is \emph{equivalent} to robustness to input in any nonlinear recurrent neural network that may or may not be in the gambit of reservoir computing. Further, backed by theoretical conclusions, we define and find the difficult-to-describe \emph{input specific} edge-of-criticality or the echo state property threshold, which defines the boundary between parameter related stability and instability.