Types of Relations: Defining Analogies with Category Theory

In order to behave intelligently both humans and machines have to represent their knowledge adequately for how it is used. Humans often use analogies to transfer their knowledge to new domains, or help others with this transfer via explanations. Hence, an important question is: What representation can be used to construct, find, and evaluate analogies? In this paper, we study features of a domain that are important for constructing analogies. We do so by formalizing knowledge domains as categories. We use the well-known example of the analogy between the solar system and the hydrogen atom to demonstrate how to construct domain categories. We also show how functors, pullbacks, and pushouts can be used to define an analogy, describe its core and a corresponding blend of the underlying domains.

Solving Bongard Problems with a Visual Language and Pragmatic Reasoning

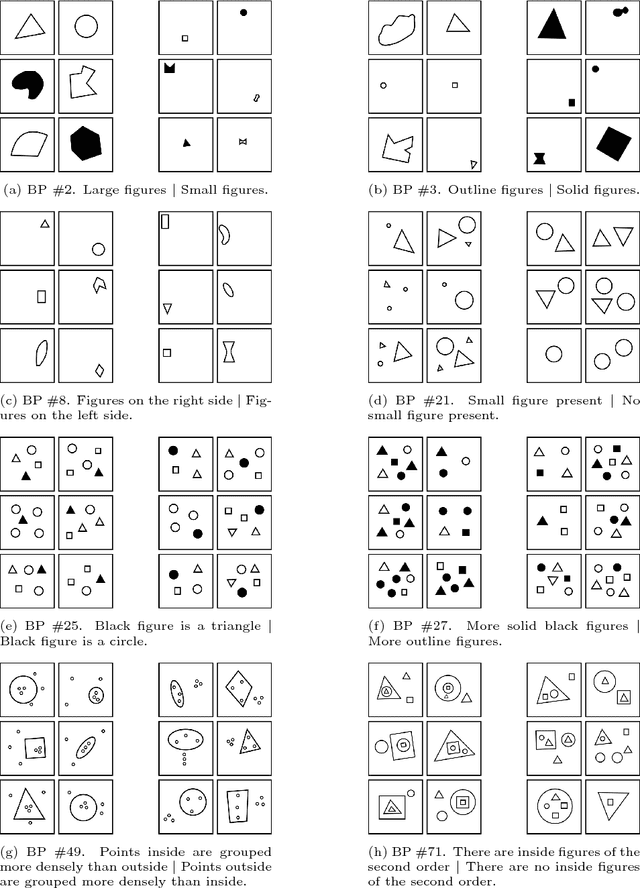
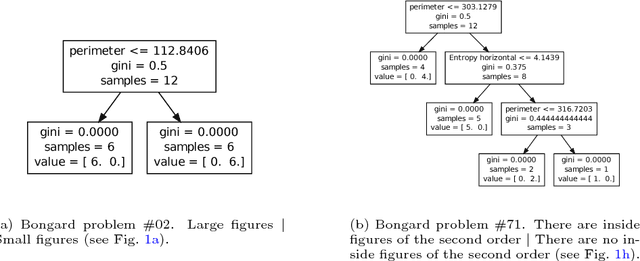
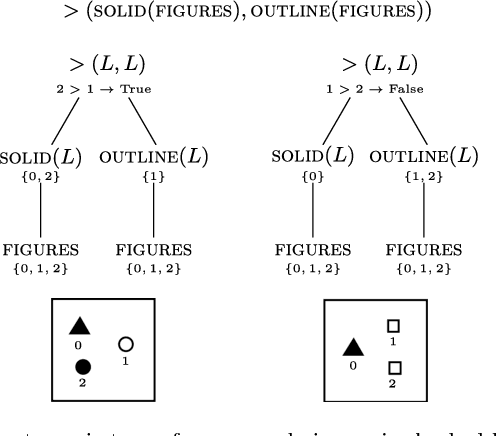
More than 50 years ago Bongard introduced 100 visual concept learning problems as a testbed for intelligent vision systems. These problems are now known as Bongard problems. Although they are well known in the cognitive science and AI communities only moderate progress has been made towards building systems that can solve a substantial subset of them. In the system presented here, visual features are extracted through image processing and then translated into a symbolic visual vocabulary. We introduce a formal language that allows representing complex visual concepts based on this vocabulary. Using this language and Bayesian inference, complex visual concepts can be induced from the examples that are provided in each Bongard problem. Contrary to other concept learning problems the examples from which concepts are induced are not random in Bongard problems, instead they are carefully chosen to communicate the concept, hence requiring pragmatic reasoning. Taking pragmatic reasoning into account we find good agreement between the concepts with high posterior probability and the solutions formulated by Bongard himself. While this approach is far from solving all Bongard problems, it solves the biggest fraction yet.