Florentin Smarandache
Editors
Answers to Imamura Note on the Definition of Neutrosophic Logic
Nov 24, 2018Abstract:In order to more accurately situate and fit the neutrosophic logic into the framework of nonstandard analysis, we present the neutrosophic inequalities, neutrosophic equality, neutrosophic infimum and supremum, neutrosophic standard intervals, including the cases when the neutrosophic logic standard and nonstandard components T, I, F get values outside of the classical real unit interval [0, 1], and a brief evolution of neutrosophic operators. The paper intends to answer Imamura criticism that we found benefic in better understanding the nonstandard neutrosophic logic, although the nonstandard neutrosophic logic was never used in practical applications.
Plithogeny, Plithogenic Set, Logic, Probability, and Statistics
Aug 12, 2018



Abstract:In this book we introduce the plithogenic set (as generalization of crisp, fuzzy, intuitionistic fuzzy, and neutrosophic sets), plithogenic logic (as generalization of classical, fuzzy, intuitionistic fuzzy, and neutrosophic logics), plithogenic probability (as generalization of classical, imprecise, and neutrosophic probabilities), and plithogenic statistics (as generalization of classical, and neutrosophic statistics). Plithogenic Set is a set whose elements are characterized by one or more attributes, and each attribute may have many values. An attribute value v has a corresponding (fuzzy, intuitionistic fuzzy, or neutrosophic) degree of appurtenance d(x,v) of the element x, to the set P, with respect to some given criteria. In order to obtain a better accuracy for the plithogenic aggregation operators in the plithogenic set, logic, probability and for a more exact inclusion (partial order), a (fuzzy, intuitionistic fuzzy, or neutrosophic) contradiction (dissimilarity) degree is defined between each attribute value and the dominant (most important) attribute value. The plithogenic intersection and union are linear combinations of the fuzzy operators tnorm and tconorm, while the plithogenic complement, inclusion, equality are influenced by the attribute values contradiction (dissimilarity) degrees. Formal definitions of plithogenic set, logic, probability, statistics are presented into the book, followed by plithogenic aggregation operators, various theorems related to them, and afterwards examples and applications of these new concepts in our everyday life.
New Trends in Neutrosophic Theory and Applications
Nov 23, 2016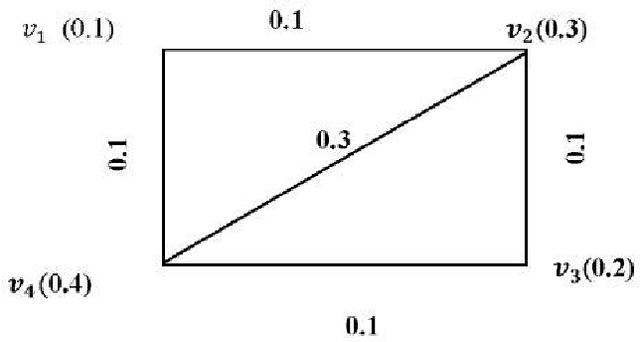


Abstract:Neutrosophic theory and applications have been expanding in all directions at an astonishing rate especially after the introduction the journal entitled Neutrosophic Sets and Systems. New theories, techniques, algorithms have been rapidly developed. One of the most striking trends in the neutrosophic theory is the hybridization of neutrosophic set with other potential sets such as rough set, bipolar set, soft set, hesitant fuzzy set, etc. The different hybrid structure such as rough neutrosophic set, single valued neutrosophic rough set, bipolar neutrosophic set, single valued neutrosophic hesitant fuzzy set, etc. are proposed in the literature in a short period of time. Neutrosophic set has been a very important tool in all various areas of data mining, decision making, e-learning, engineering, medicine, social science, and some more. The book New Trends in Neutrosophic Theories and Applications focuses on theories, methods, algorithms for decision making and also applications involving neutrosophic information. Some topics deal with data mining, decision making, e-learning, graph theory, medical diagnosis, probability theory, topology, and some more.
* 424 pages
Strong Neutrosophic Graphs and Subgraph Topological Subspaces
Oct 30, 2016



Abstract:In this book authors for the first time introduce the notion of strong neutrosophic graphs. They are very different from the usual graphs and neutrosophic graphs. Using these new structures special subgraph topological spaces are defined. Further special lattice graph of subgraphs of these graphs are defined and described. Several interesting properties using subgraphs of a strong neutrosophic graph are obtained. Several open conjectures are proposed. These new class of strong neutrosophic graphs will certainly find applications in Neutrosophic Cognitive Maps (NCM), Neutrosophic Relational Maps (NRM) and Neutrosophic Relational Equations (NRE) with appropriate modifications.
Neutrosophic Overset, Neutrosophic Underset, and Neutrosophic Offset. Similarly for Neutrosophic Over-/Under-/Off- Logic, Probability, and Statistics
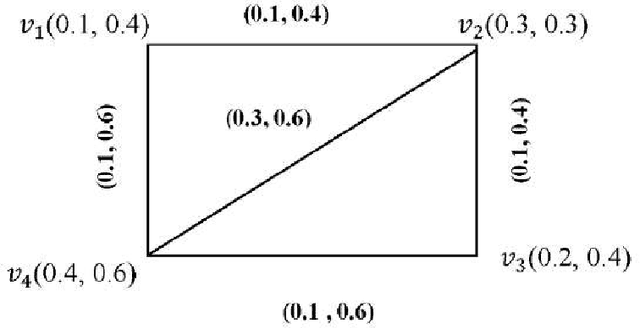
Jun 30, 2016
Abstract:Neutrosophic Over-/Under-/Off-Set and -Logic were defined by the author in 1995 and published for the first time in 2007. We extended the neutrosophic set respectively to Neutrosophic Overset {when some neutrosophic component is over 1}, Neutrosophic Underset {when some neutrosophic component is below 0}, and to Neutrosophic Offset {when some neutrosophic components are off the interval [0, 1], i.e. some neutrosophic component over 1 and other neutrosophic component below 0}. This is no surprise with respect to the classical fuzzy set/logic, intuitionistic fuzzy set/logic, or classical/imprecise probability, where the values are not allowed outside the interval [0, 1], since our real-world has numerous examples and applications of over-/under-/off-neutrosophic components. For example, person working overtime deserves a membership degree over 1, while a person producing more damage than benefit to a company deserves a membership below 0. Then, similarly, the Neutrosophic Logic/Measure/Probability/Statistics etc. were extended to respectively Neutrosophic Over-/Under-/Off-Logic, -Measure, -Probability, -Statistics etc. [Smarandache, 2007].
* 170 pages
Symbolic Neutrosophic Theory
Oct 18, 2015



Abstract:Symbolic (or Literal) Neutrosophic Theory is referring to the use of abstract symbols (i.e. the letters T, I, F, or their refined indexed letters Tj, Ik, Fl) in neutrosophics. We extend the dialectical triad thesis-antithesis-synthesis to the neutrosophic tetrad thesis-antithesis-neutrothesis-neutrosynthesis. The we introduce the neutrosophic system that is a quasi or (t,i,f) classical system, in the sense that the neutrosophic system deals with quasi-terms (concepts, attributes, etc.). Then the notions of Neutrosophic Axiom, Neutrosophic Deducibility, Degree of Contradiction (Dissimilarity) of Two Neutrosophic Axioms, etc. Afterwards a new type of structures, called (t, i, f) Neutrosophic Structures, and we show particular cases of such structures in geometry and in algebra. Also, a short history of the neutrosophic set, neutrosophic numerical components and neutrosophic literal components, neutrosophic numbers, etc. We construct examples of splitting the literal indeterminacy (I) into literal subindeterminacies (I1, I2, and so on, Ir), and to define a multiplication law of these literal subindeterminacies in order to be able to build refined I neutrosophic algebraic structures. We define three neutrosophic actions and their properties. We then introduce the prevalence order on T,I,F with respect to a given neutrosophic operator. And the refinement of neutrosophic entities A, neutA, and antiA. Then we extend the classical logical operators to neutrosophic literal (symbolic) logical operators and to refined literal (symbolic) logical operators, and we define the refinement neutrosophic literal (symbolic) space. We introduce the neutrosophic quadruple numbers (a+bT+cI+dF) and the refined neutrosophic quadruple numbers. Then we define an absorbance law, based on a prevalence order, in order to multiply the neutrosophic quadruple numbers.
$α$-Discounting Multi-Criteria Decision Making ($α$-D MCDM)
Oct 02, 2015Abstract:In this book we introduce a new procedure called \alpha-Discounting Method for Multi-Criteria Decision Making (\alpha-D MCDM), which is as an alternative and extension of Saaty Analytical Hierarchy Process (AHP). It works for any number of preferences that can be transformed into a system of homogeneous linear equations. A degree of consistency (and implicitly a degree of inconsistency) of a decision-making problem are defined. \alpha-D MCDM is afterwards generalized to a set of preferences that can be transformed into a system of linear and or non-linear homogeneous and or non-homogeneous equations and or inequalities. The general idea of \alpha-D MCDM is to assign non-null positive parameters \alpha_1, \alpha_2, and so on \alpha_p to the coefficients in the right-hand side of each preference that diminish or increase them in order to transform the above linear homogeneous system of equations which has only the null-solution, into a system having a particular non-null solution. After finding the general solution of this system, the principles used to assign particular values to all parameters \alpha is the second important part of \alpha-D, yet to be deeper investigated in the future. In the current book we propose the Fairness Principle, i.e. each coefficient should be discounted with the same percentage (we think this is fair: not making any favoritism or unfairness to any coefficient), but the reader can propose other principles. For consistent decision-making problems with pairwise comparisons, \alpha-Discounting Method together with the Fairness Principle give the same result as AHP. But for weak inconsistent decision-making problem, \alpha-Discounting together with the Fairness Principle give a different result from AHP. Many consistent, weak inconsistent, and strong inconsistent examples are given in this book.
* 62 pages
Unification of Fusion Theories, Rules, Filters, Image Fusion and Target Tracking Methods (UFT)
Jul 27, 2015



Abstract:The author has pledged in various papers, conference or seminar presentations, and scientific grant applications (between 2004-2015) for the unification of fusion theories, combinations of fusion rules, image fusion procedures, filter algorithms, and target tracking methods for more accurate applications to our real world problems - since neither fusion theory nor fusion rule fully satisfy all needed applications. For each particular application, one selects the most appropriate fusion space and fusion model, then the fusion rules, and the algorithms of implementation. He has worked in the Unification of the Fusion Theories (UFT), which looks like a cooking recipe, better one could say like a logical chart for a computer programmer, but one does not see another method to comprise/unify all things. The unification scenario presented herein, which is now in an incipient form, should periodically be updated incorporating new discoveries from the fusion and engineering research.
* 79 pages, a diagram. arXiv admin note: substantial text overlap with arXiv:cs/0409040, arXiv:0901.1289, arXiv:cs/0410033
Soft Neutrosophic Algebraic Structures and Their Generalization
Aug 23, 2014Abstract:Study of soft sets was first proposed by Molodtsov in 1999 to deal with uncertainty in a non-parametric manner. The researchers did not pay attention to soft set theory at that time but now the soft set theory has been developed in many areas of mathematics. Algebraic structures using soft set theory are very rapidly developed. In this book we developed soft neutrosophic algebraic structures by using soft sets and neutrosophic algebraic structures. In this book we study soft neutrosophic groups, soft neutrosophic semigroups, soft neutrosophic loops, soft neutrosophic LA-semigroups, and their generalizations respectively.
n-Valued Refined Neutrosophic Logic and Its Applications to Physics
Jul 03, 2014
Abstract:In this paper we present a short history of logics: from particular cases of 2-symbol or numerical valued logic to the general case of n-symbol or numerical valued logic. We show generalizations of 2-valued Boolean logic to fuzzy logic, also from the Kleene and Lukasiewicz 3-symbol valued logics or Belnap 4-symbol valued logic to the most general n-symbol or numerical valued refined neutrosophic logic. Two classes of neutrosophic norm (n-norm) and neutrosophic conorm (n-conorm) are defined. Examples of applications of neutrosophic logic to physics are listed in the last section. Similar generalizations can be done for n-Valued Refined Neutrosophic Set, and respectively n- Valued Refined Neutrosopjhic Probability.
* 9 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge