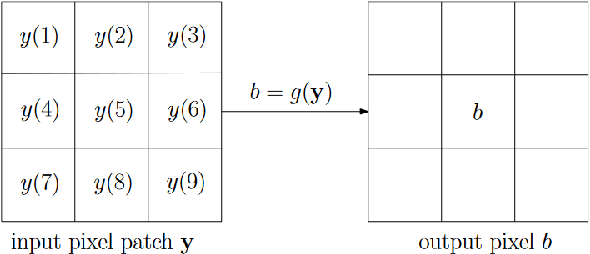
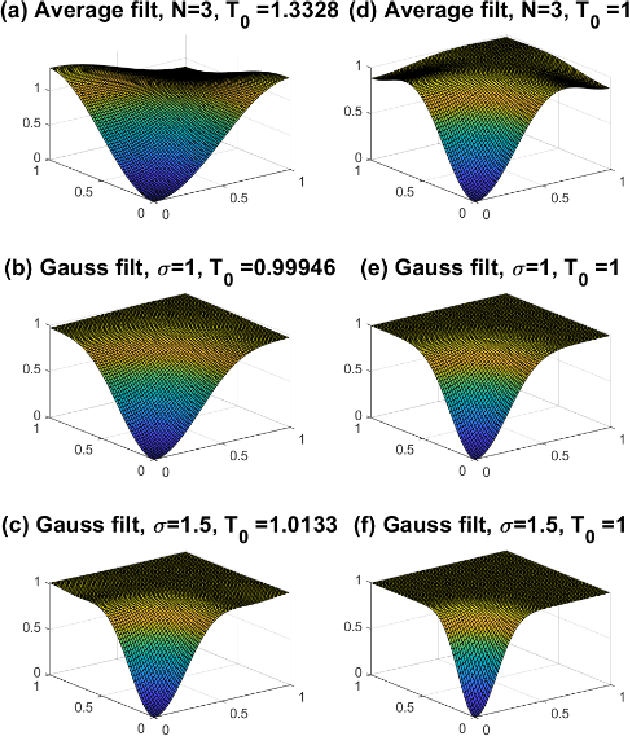
Reverse image filtering using total derivative approximation and accelerated gradient descent

In this paper, we address a new problem of reversing the effect of an image filter, which can be linear or nonlinear. The assumption is that the algorithm of the filter is unknown and the filter is available as a black box. We formulate this inverse problem as minimizing a local patch-based cost function and use total derivative to approximate the gradient which is used in gradient descent to solve the problem. We analyze factors affecting the convergence and quality of the output in the Fourier domain. We also study the application of accelerated gradient descent algorithms in three gradient-free reverse filters, including the one proposed in this paper. We present results from extensive experiments to evaluate the complexity and effectiveness of the proposed algorithm. Results demonstrate that the proposed algorithm outperforms the state-of-the-art in that (1) it is at the same level of complexity as that of the fastest reverse filter, but it can reverse a larger number of filters, and (2) it can reverse the same list of filters as that of the very complex reverse filter, but its complexity is much smaller.

A guided edge-aware smoothing-sharpening filter based on patch interpolation model and generalized Gamma distribution

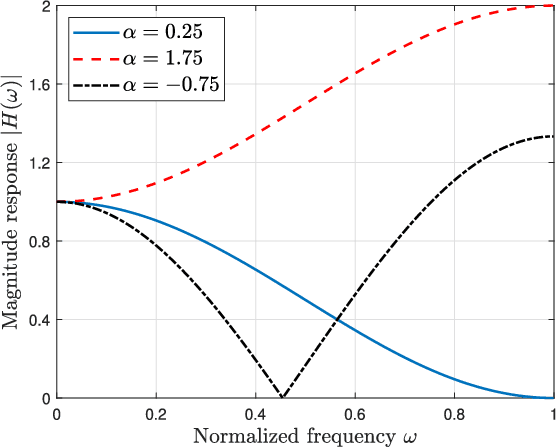
Smoothing and sharpening are two fundamental image processing operations. The latter is usually related to the former through the unsharp masking algorithm. In this paper, we develop a new type of filter which performs smoothing or sharpening via a tuning parameter. The development of the new filter is based on (1) a new Laplacian-based filter formulation which unifies the smoothing and sharpening operations, (2) a patch interpolation model similar to that used in the guided filter which provides edge-awareness capability, and (3) the generalized Gamma distribution which is used as the prior for parameter estimation. We have conducted detailed studies on the properties of two versions of the proposed filter (self-guidance and external guidance). We have also conducted experiments to demonstrate applications of the proposed filter. In the self-guidance case, we have developed adaptive smoothing and sharpening algorithms based on texture, depth and blurriness information extracted from an image. Applications include enhancing human face images, producing shallow depth of field effects, focus-based image enhancement, and seam carving. In the external guidance case, we have developed new algorithms for combining flash and no-flash images and for enhancing multi-spectral images using a panchromatic image.

Single image deep defocus estimation and its applications

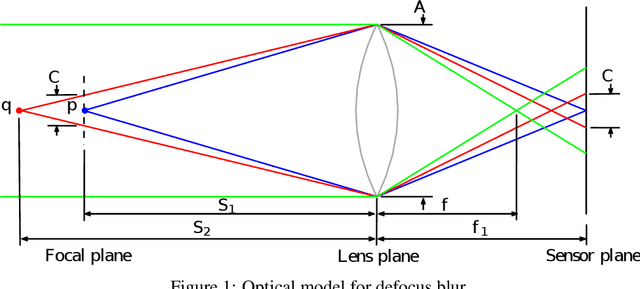
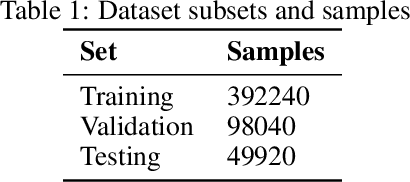
The depth information is useful in many image processing applications. However, since taking a picture is a process of projection of a 3D scene onto a 2D imaging sensor, the depth information is embedded in the image. Extracting the depth information from the image is a challenging task. A guiding principle is that the level of blurriness due to defocus is related to the distance between the object and the focal plane. Based on this principle and the widely used assumption that Gaussian blur is a good model for defocus blur, we formulate the problem of estimating the spatially varying defocus blurriness as a Gaussian blur classification problem. We solved the problem by training a deep neural network to classify image patches into one of the 20 levels of blurriness. We have created a dataset of more than 500000 image patches of size 32x32 which are used to train and test several well-known network models. We find that MobileNetV2 is suitable for this application due to its low memory requirement and high accuracy. The trained model is used to determine the patch blurriness which is then refined by applying an iterative weighted guided filter. The result is a defocus map that carries the information of the degree of blurriness for each pixel. We compare the proposed method with state-of-the-art techniques and we demonstrate its successful applications in adaptive image enhancement, defocus magnification, and multi-focus image fusion.