FlowMixer: A Constrained Neural Architecture for Interpretable Spatiotemporal Forecasting

We introduce FlowMixer, a neural architecture that leverages constrained matrix operations to model structured spatiotemporal patterns. At its core, FlowMixer incorporates non-negative matrix mixing layers within a reversible mapping framework-applying transforms before mixing and their inverses afterward. This shape-preserving design enables a Kronecker-Koopman eigenmode framework that bridges statistical learning with dynamical systems theory, providing interpretable spatiotemporal patterns and facilitating direct algebraic manipulation of prediction horizons without retraining. Extensive experiments across diverse domains demonstrate FlowMixer's robust long-horizon forecasting capabilities while effectively modeling physical phenomena such as chaotic attractors and turbulent flows. These results suggest that architectural constraints can simultaneously enhance predictive performance and mathematical interpretability in neural forecasting systems.

Catastrophic Overfitting, Entropy Gap and Participation Ratio: A Noiseless $l^p$ Norm Solution for Fast Adversarial Training

Adversarial training is a cornerstone of robust deep learning, but fast methods like the Fast Gradient Sign Method (FGSM) often suffer from Catastrophic Overfitting (CO), where models become robust to single-step attacks but fail against multi-step variants. While existing solutions rely on noise injection, regularization, or gradient clipping, we propose a novel solution that purely controls the $l^p$ training norm to mitigate CO. Our study is motivated by the empirical observation that CO is more prevalent under the $l^{\infty}$ norm than the $l^2$ norm. Leveraging this insight, we develop a framework for generalized $l^p$ attack as a fixed point problem and craft $l^p$-FGSM attacks to understand the transition mechanics from $l^2$ to $l^{\infty}$. This leads to our core insight: CO emerges when highly concentrated gradients where information localizes in few dimensions interact with aggressive norm constraints. By quantifying gradient concentration through Participation Ratio and entropy measures, we develop an adaptive $l^p$-FGSM that automatically tunes the training norm based on gradient information. Extensive experiments demonstrate that this approach achieves strong robustness without requiring additional regularization or noise injection, providing a novel and theoretically-principled pathway to mitigate the CO problem.

Urban traffic analysis and forecasting through shared Koopman eigenmodes

Predicting traffic flow in data-scarce cities is challenging due to limited historical data. To address this, we leverage transfer learning by identifying periodic patterns common to data-rich cities using a customized variant of Dynamic Mode Decomposition (DMD): constrained Hankelized DMD (TrHDMD). This method uncovers common eigenmodes (urban heartbeats) in traffic patterns and transfers them to data-scarce cities, significantly enhancing prediction performance. TrHDMD reduces the need for extensive training datasets by utilizing prior knowledge from other cities. By applying Koopman operator theory to multi-city loop detector data, we identify stable, interpretable, and time-invariant traffic modes. Injecting ``urban heartbeats'' into forecasting tasks improves prediction accuracy and has the potential to enhance traffic management strategies for cities with varying data infrastructures. Our work introduces cross-city knowledge transfer via shared Koopman eigenmodes, offering actionable insights and reliable forecasts for data-scarce urban environments.

Exact Stochastic Second Order Deep Learning

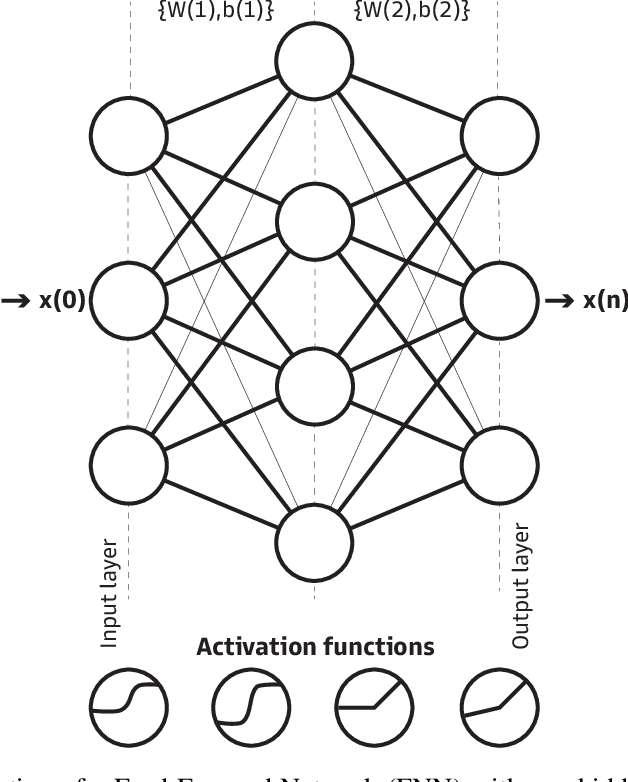
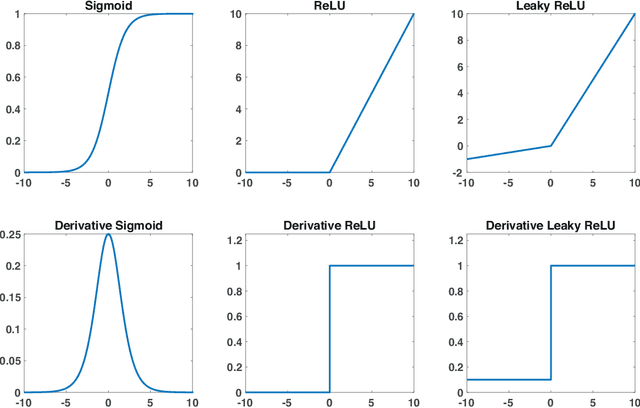
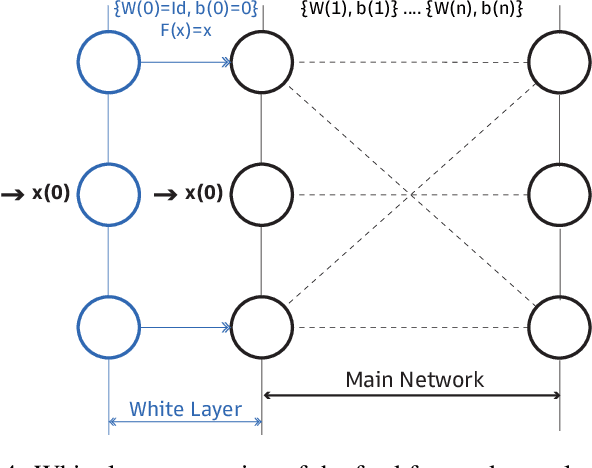
Optimization in Deep Learning is mainly dominated by first-order methods which are built around the central concept of backpropagation. Second-order optimization methods, which take into account the second-order derivatives are far less used despite superior theoretical properties. This inadequacy of second-order methods stems from its exorbitant computational cost, poor performance, and the ineluctable non-convex nature of Deep Learning. Several attempts were made to resolve the inadequacy of second-order optimization without reaching a cost-effective solution, much less an exact solution. In this work, we show that this long-standing problem in Deep Learning could be solved in the stochastic case, given a suitable regularization of the neural network. Interestingly, we provide an expression of the stochastic Hessian and its exact eigenvalues. We provide a closed-form formula for the exact stochastic second-order Newton direction, we solve the non-convexity issue and adjust our exact solution to favor flat minima through regularization and spectral adjustment. We test our exact stochastic second-order method on popular datasets and reveal its adequacy for Deep Learning.