Fisher Discriminant Triplet and Contrastive Losses for Training Siamese Networks

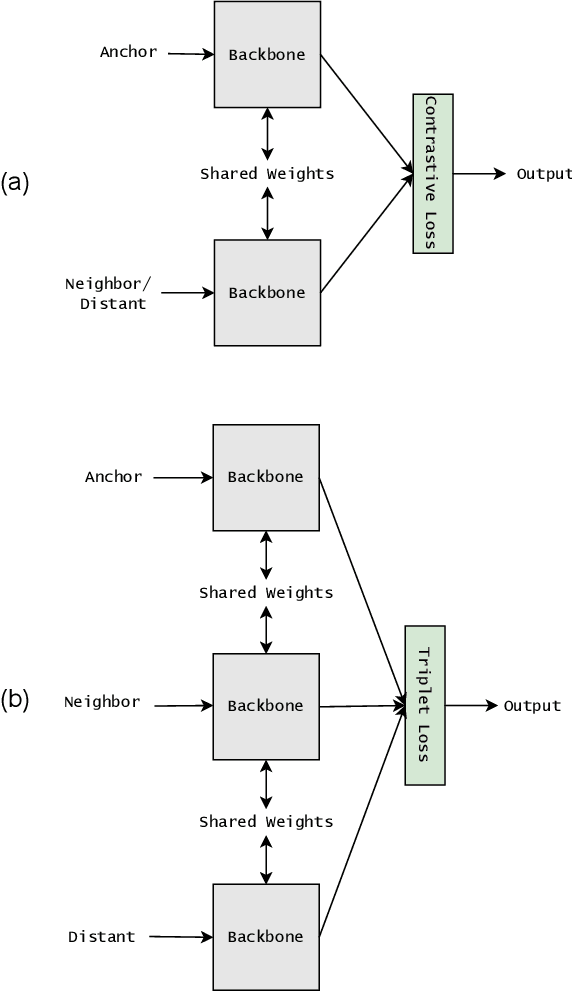
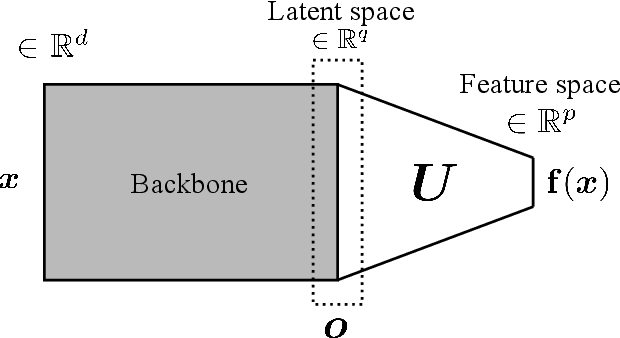
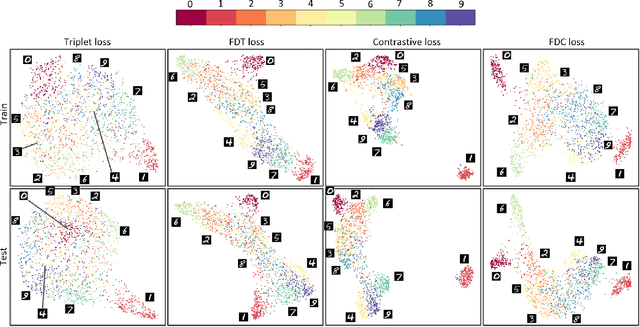
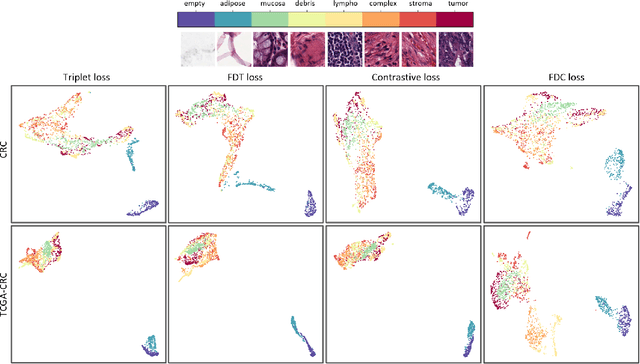
Siamese neural network is a very powerful architecture for both feature extraction and metric learning. It usually consists of several networks that share weights. The Siamese concept is topology-agnostic and can use any neural network as its backbone. The two most popular loss functions for training these networks are the triplet and contrastive loss functions. In this paper, we propose two novel loss functions, named Fisher Discriminant Triplet (FDT) and Fisher Discriminant Contrastive (FDC). The former uses anchor-neighbor-distant triplets while the latter utilizes pairs of anchor-neighbor and anchor-distant samples. The FDT and FDC loss functions are designed based on the statistical formulation of the Fisher Discriminant Analysis (FDA), which is a linear subspace learning method. Our experiments on the MNIST and two challenging and publicly available histopathology datasets show the effectiveness of the proposed loss functions.

Theoretical Insights into the Use of Structural Similarity Index In Generative Models and Inferential Autoencoders

Generative models and inferential autoencoders mostly make use of $\ell_2$ norm in their optimization objectives. In order to generate perceptually better images, this short paper theoretically discusses how to use Structural Similarity Index (SSIM) in generative models and inferential autoencoders. We first review SSIM, SSIM distance metrics, and SSIM kernel. We show that the SSIM kernel is a universal kernel and thus can be used in unconditional and conditional generated moment matching networks. Then, we explain how to use SSIM distance in variational and adversarial autoencoders and unconditional and conditional Generative Adversarial Networks (GANs). Finally, we propose to use SSIM distance rather than $\ell_2$ norm in least squares GAN.

Weighted Fisher Discriminant Analysis in the Input and Feature Spaces

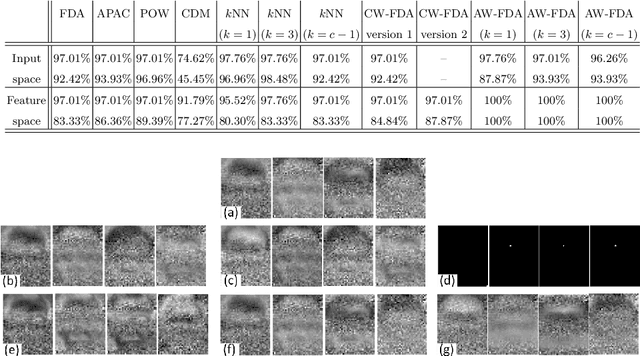
Fisher Discriminant Analysis (FDA) is a subspace learning method which minimizes and maximizes the intra- and inter-class scatters of data, respectively. Although, in FDA, all the pairs of classes are treated the same way, some classes are closer than the others. Weighted FDA assigns weights to the pairs of classes to address this shortcoming of FDA. In this paper, we propose a cosine-weighted FDA as well as an automatically weighted FDA in which weights are found automatically. We also propose a weighted FDA in the feature space to establish a weighted kernel FDA for both existing and newly proposed weights. Our experiments on the ORL face recognition dataset show the effectiveness of the proposed weighting schemes.

Roweis Discriminant Analysis: A Generalized Subspace Learning Method

We present a new method which generalizes subspace learning based on eigenvalue and generalized eigenvalue problems. This method, Roweis Discriminant Analysis (RDA), is named after Sam Roweis to whom the field of subspace learning owes significantly. RDA is a family of infinite number of algorithms where Principal Component Analysis (PCA), Supervised PCA (SPCA), and Fisher Discriminant Analysis (FDA) are special cases. One of the extreme special cases, which we name Double Supervised Discriminant Analysis (DSDA), uses the labels twice; it is novel and has not appeared elsewhere. We propose a dual for RDA for some special cases. We also propose kernel RDA, generalizing kernel PCA, kernel SPCA, and kernel FDA, using both dual RDA and representation theory. Our theoretical analysis explains previously known facts such as why SPCA can use regression but FDA cannot, why PCA and SPCA have duals but FDA does not, why kernel PCA and kernel SPCA use kernel trick but kernel FDA does not, and why PCA is the best linear method for reconstruction. Roweisfaces and kernel Roweisfaces are also proposed generalizing eigenfaces, Fisherfaces, supervised eigenfaces, and their kernel variants. We also report experiments showing the effectiveness of RDA and kernel RDA on some benchmark datasets.

Quantized Fisher Discriminant Analysis

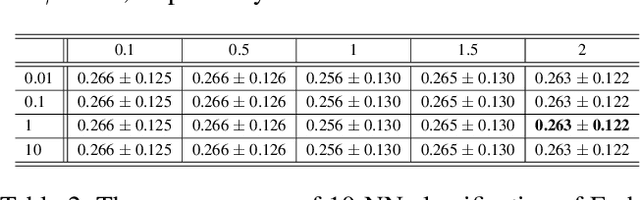
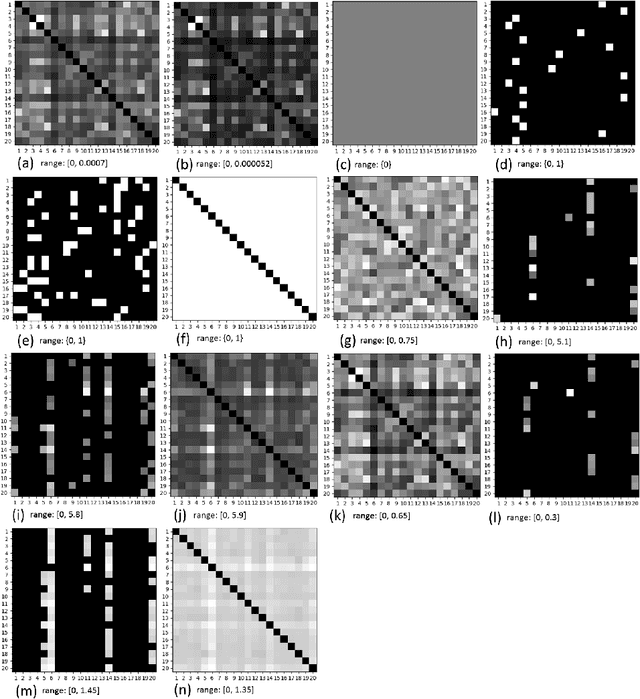
This paper proposes a new subspace learning method, named Quantized Fisher Discriminant Analysis (QFDA), which makes use of both machine learning and information theory. There is a lack of literature for combination of machine learning and information theory and this paper tries to tackle this gap. QFDA finds a subspace which discriminates the uniformly quantized images in the Discrete Cosine Transform (DCT) domain at least as well as discrimination of non-quantized images by Fisher Discriminant Analysis (FDA) while the images have been compressed. This helps the user to throw away the original images and keep the compressed images instead without noticeable loss of classification accuracy. We propose a cost function whose minimization can be interpreted as rate-distortion optimization in information theory. We also propose quantized Fisherfaces for facial analysis in QFDA. Our experiments on AT&T face dataset and Fashion MNIST dataset show the effectiveness of this subspace learning method.

Locally Linear Image Structural Embedding for Image Structure Manifold Learning

Most of existing manifold learning methods rely on Mean Squared Error (MSE) or $\ell_2$ norm. However, for the problem of image quality assessment, these are not promising measure. In this paper, we introduce the concept of an image structure manifold which captures image structure features and discriminates image distortions. We propose a new manifold learning method, Locally Linear Image Structural Embedding (LLISE), and kernel LLISE for learning this manifold. The LLISE is inspired by Locally Linear Embedding (LLE) but uses SSIM rather than MSE. This paper builds a bridge between manifold learning and image fidelity assessment and it can open a new area for future investigations.

Principal Component Analysis Using Structural Similarity Index for Images

Despite the advances of deep learning in specific tasks using images, the principled assessment of image fidelity and similarity is still a critical ability to develop. As it has been shown that Mean Squared Error (MSE) is insufficient for this task, other measures have been developed with one of the most effective being Structural Similarity Index (SSIM). Such measures can be used for subspace learning but existing methods in machine learning, such as Principal Component Analysis (PCA), are based on Euclidean distance or MSE and thus cannot properly capture the structural features of images. In this paper, we define an image structure subspace which discriminates different types of image distortions. We propose Image Structural Component Analysis (ISCA) and also kernel ISCA by using SSIM, rather than Euclidean distance, in the formulation of PCA. This paper provides a bridge between image quality assessment and manifold learning opening a broad new area for future research.

Fisher and Kernel Fisher Discriminant Analysis: Tutorial

This is a detailed tutorial paper which explains the Fisher discriminant Analysis (FDA) and kernel FDA. We start with projection and reconstruction. Then, one- and multi-dimensional FDA subspaces are covered. Scatters in two- and then multi-classes are explained in FDA. Then, we discuss on the rank of the scatters and the dimensionality of the subspace. A real-life example is also provided for interpreting FDA. Then, possible singularity of the scatter is discussed to introduce robust FDA. PCA and FDA directions are also compared. We also prove that FDA and linear discriminant analysis are equivalent. Fisher forest is also introduced as an ensemble of fisher subspaces useful for handling data with different features and dimensionality. Afterwards, kernel FDA is explained for both one- and multi-dimensional subspaces with both two- and multi-classes. Finally, some simulations are performed on AT&T face dataset to illustrate FDA and compare it with PCA.

Feature Selection and Feature Extraction in Pattern Analysis: A Literature Review

Pattern analysis often requires a pre-processing stage for extracting or selecting features in order to help the classification, prediction, or clustering stage discriminate or represent the data in a better way. The reason for this requirement is that the raw data are complex and difficult to process without extracting or selecting appropriate features beforehand. This paper reviews theory and motivation of different common methods of feature selection and extraction and introduces some of their applications. Some numerical implementations are also shown for these methods. Finally, the methods in feature selection and extraction are compared.

Eigenvalue and Generalized Eigenvalue Problems: Tutorial

This paper is a tutorial for eigenvalue and generalized eigenvalue problems. We first introduce eigenvalue problem, eigen-decomposition (spectral decomposition), and generalized eigenvalue problem. Then, we mention the optimization problems which yield to the eigenvalue and generalized eigenvalue problems. We also provide examples from machine learning, including principal component analysis, kernel supervised principal component analysis, and Fisher discriminant analysis, which result in eigenvalue and generalized eigenvalue problems. Finally, we introduce the solutions to both eigenvalue and generalized eigenvalue problems.