Scattering Networks on Noncommutative Finite Groups

Scattering Networks were initially designed to elucidate the behavior of early layers in Convolutional Neural Networks (CNNs) over Euclidean spaces and are grounded in wavelets. In this work, we introduce a scattering transform on an arbitrary finite group (not necessarily abelian) within the context of group-equivariant convolutional neural networks (G-CNNs). We present wavelets on finite groups and analyze their similarity to classical wavelets. We demonstrate that, under certain conditions in the wavelet coefficients, the scattering transform is non-expansive, stable under deformations, preserves energy, equivariant with respect to left and right group translations, and, as depth increases, the scattering coefficients are less sensitive to group translations of the signal, all desirable properties of convolutional neural networks. Furthermore, we provide examples illustrating the application of the scattering transform to classify data with domains involving abelian and nonabelian groups.

Learning optimal smooth invariant subspaces for data approximation

In this article, we consider the problem of approximating a finite set of data (usually huge in applications) by invariant subspaces generated through a small set of smooth functions. The invariance is either by translations under a full-rank lattice or through the action of crystallographic groups. Smoothness is ensured by stipulating that the generators belong to a Paley-Wiener space, that is selected in an optimal way based on the characteristics of the given data. To complete our investigation, we analyze the fundamental role played by the lattice in the process of approximation.

Optimal translational-rotational invariant dictionaries for images

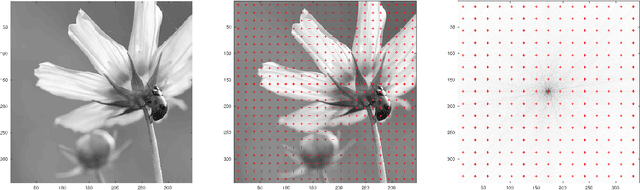
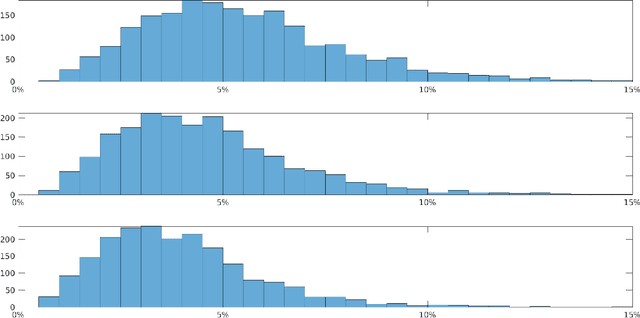
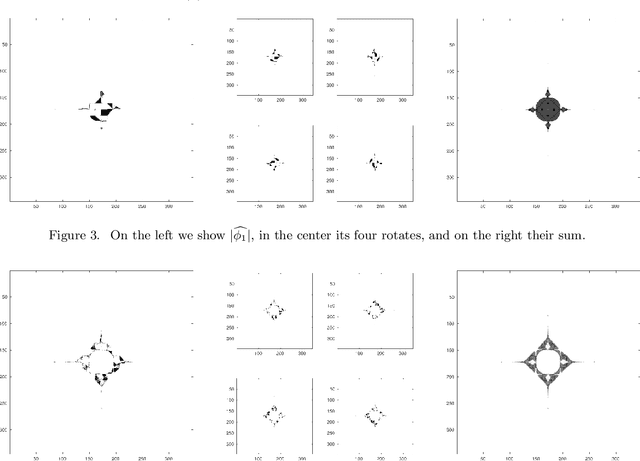
We provide the construction of a set of square matrices whose translates and rotates provide a Parseval frame that is optimal for approximating a given dataset of images. Our approach is based on abstract harmonic analysis techniques. Optimality is considered with respect to the quadratic error of approximation of the images in the dataset with their projection onto a linear subspace that is invariant under translations and rotations. In addition, we provide an elementary and fully self-contained proof of optimality, and the numerical results from datasets of natural images.