On the Evaluation of Engineering Artificial General Intelligence

We discuss the challenges and propose a framework for evaluating engineering artificial general intelligence (eAGI) agents. We consider eAGI as a specialization of artificial general intelligence (AGI), deemed capable of addressing a broad range of problems in the engineering of physical systems and associated controllers. We exclude software engineering for a tractable scoping of eAGI and expect dedicated software engineering AI agents to address the software implementation challenges. Similar to human engineers, eAGI agents should possess a unique blend of background knowledge (recall and retrieve) of facts and methods, demonstrate familiarity with tools and processes, exhibit deep understanding of industrial components and well-known design families, and be able to engage in creative problem solving (analyze and synthesize), transferring ideas acquired in one context to another. Given this broad mandate, evaluating and qualifying the performance of eAGI agents is a challenge in itself and, arguably, a critical enabler to developing eAGI agents. In this paper, we address this challenge by proposing an extensible evaluation framework that specializes and grounds Bloom's taxonomy - a framework for evaluating human learning that has also been recently used for evaluating LLMs - in an engineering design context. Our proposed framework advances the state of the art in benchmarking and evaluation of AI agents in terms of the following: (a) developing a rich taxonomy of evaluation questions spanning from methodological knowledge to real-world design problems; (b) motivating a pluggable evaluation framework that can evaluate not only textual responses but also evaluate structured design artifacts such as CAD models and SysML models; and (c) outlining an automatable procedure to customize the evaluation benchmark to different engineering contexts.

Learning High-Dimensional Nonparametric Differential Equations via Multivariate Occupation Kernel Functions

Learning a nonparametric system of ordinary differential equations (ODEs) from $n$ trajectory snapshots in a $d$-dimensional state space requires learning $d$ functions of $d$ variables. Explicit formulations scale quadratically in $d$ unless additional knowledge about system properties, such as sparsity and symmetries, is available. In this work, we propose a linear approach to learning using the implicit formulation provided by vector-valued Reproducing Kernel Hilbert Spaces. By rewriting the ODEs in a weaker integral form, which we subsequently minimize, we derive our learning algorithm. The minimization problem's solution for the vector field relies on multivariate occupation kernel functions associated with the solution trajectories. We validate our approach through experiments on highly nonlinear simulated and real data, where $d$ may exceed 100. We further demonstrate the versatility of the proposed method by learning a nonparametric first order quasilinear partial differential equation.

Learning Nonparametric Ordinary differential Equations: Application to Sparse and Noisy Data

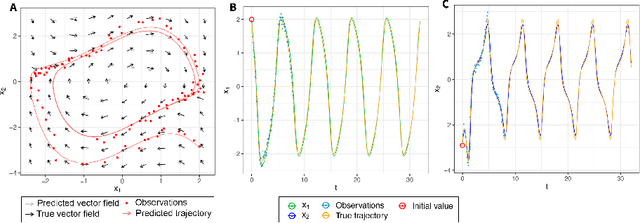
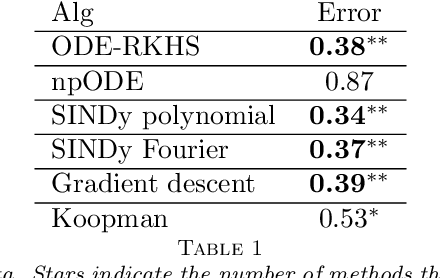
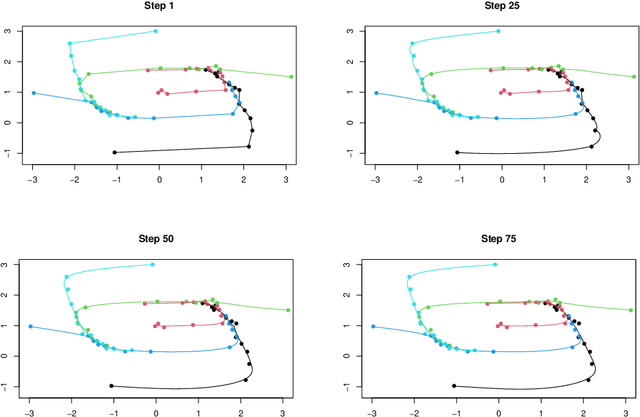
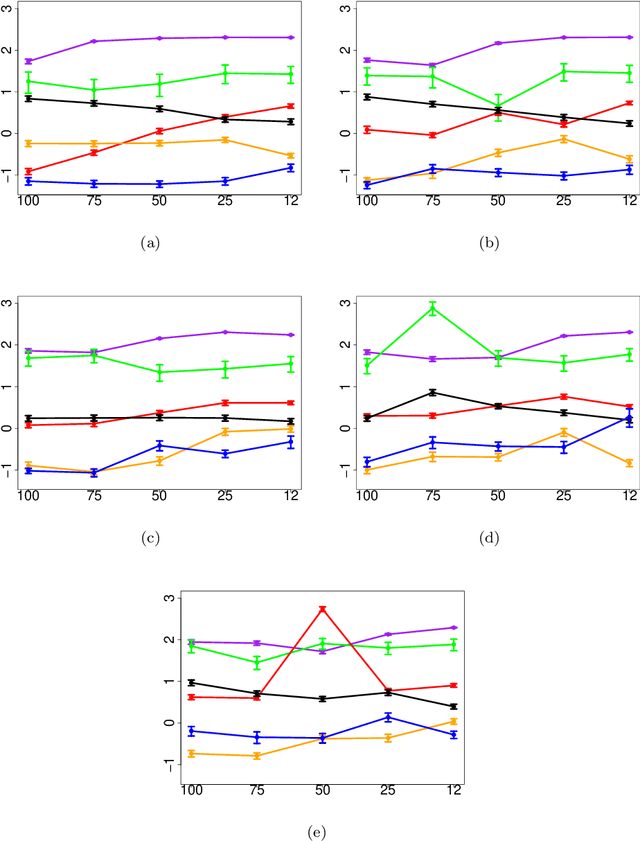
Learning nonparametric systems of Ordinary Differential Equations (ODEs) $\dot x = f(t,x)$ from noisy and sparse data is an emerging machine learning topic. We use the well-developed theory of Reproducing Kernel Hilbert Spaces (RKHS) to define candidates for $f$ for which the solution of the ODE exists and is unique. Learning $f$ consists of solving a constrained optimization problem in an RKHS. We propose a penalty method that iteratively uses the Representer theorem and Euler approximations to provide a numerical solution. We prove a generalization bound for the $L^2$ distance between $x$ and its estimator. Experiments are provided for the FitzHugh Nagumo oscillator and for the prediction of the Amyloid level in the cortex of aging subjects. In both cases, we show competitive results when compared with the state of the art.