An AI Approach for Learning the Spectrum of the Laplace-Beltrami Operator

The spectrum of the Laplace-Beltrami (LB) operator is central in geometric deep learning tasks, capturing intrinsic properties of the shape of the object under consideration. The best established method for its estimation, from a triangulated mesh of the object, is based on the Finite Element Method (FEM), and computes the top k LB eigenvalues with a complexity of O(Nk), where N is the number of points. This can render the FEM method inefficient when repeatedly applied to databases of CAD mechanical parts, or in quality control applications where part metrology is acquired as large meshes and decisions about the quality of each part are needed quickly and frequently. As a solution to this problem, we present a geometric deep learning framework to predict the LB spectrum efficiently given the CAD mesh of a part, achieving significant computational savings without sacrificing accuracy, demonstrating that the LB spectrum is learnable. The proposed Graph Neural Network architecture uses a rich set of part mesh features - including Gaussian curvature, mean curvature, and principal curvatures. In addition to our trained network, we make available, for repeatability, a large curated dataset of real-world mechanical CAD models derived from the publicly available ABC dataset used for training and testing. Experimental results show that our method reduces computation time of the LB spectrum by approximately 5 times over linear FEM while delivering competitive accuracy.

Generalized Sparse Precision Matrix Selection for Fitting Multivariate Gaussian Random Fields to Large Data Sets

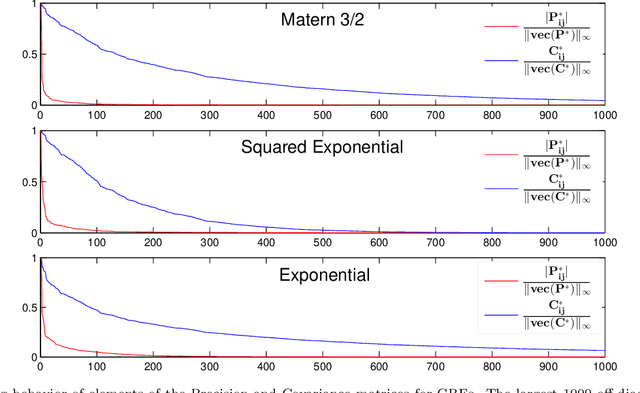
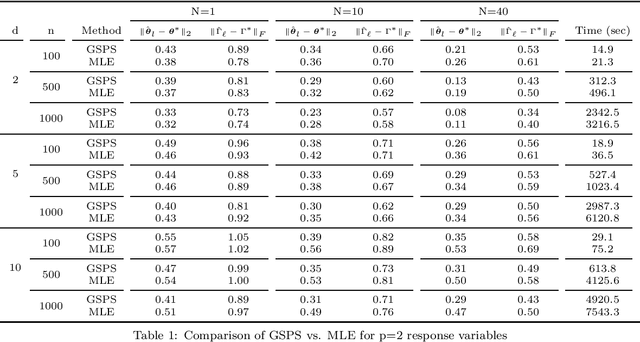
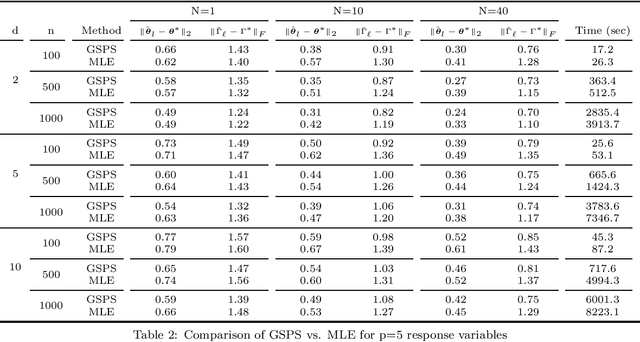
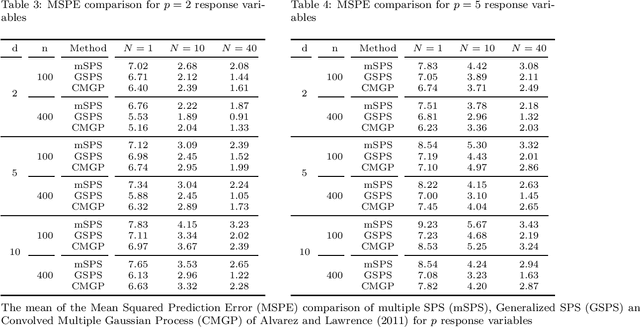
We present a new method for estimating multivariate, second-order stationary Gaussian Random Field (GRF) models based on the Sparse Precision matrix Selection (SPS) algorithm, proposed by Davanloo et al. (2015) for estimating scalar GRF models. Theoretical convergence rates for the estimated between-response covariance matrix and for the estimated parameters of the underlying spatial correlation function are established. Numerical tests using simulated and real datasets validate our theoretical findings. Data segmentation is used to handle large data sets.