Optimizing Likelihoods via Mutual Information: Bridging Simulation-Based Inference and Bayesian Optimal Experimental Design

Simulation-based inference (SBI) is a method to perform inference on a variety of complex scientific models with challenging inference (inverse) problems. Bayesian Optimal Experimental Design (BOED) aims to efficiently use experimental resources to make better inferences. Various stochastic gradient-based BOED methods have been proposed as an alternative to Bayesian optimization and other experimental design heuristics to maximize information gain from an experiment. We demonstrate a link via mutual information bounds between SBI and stochastic gradient-based variational inference methods that permits BOED to be used in SBI applications as SBI-BOED. This link allows simultaneous optimization of experimental designs and optimization of amortized inference functions. We evaluate the pitfalls of naive design optimization using this method in a standard SBI task and demonstrate the utility of a well-chosen design distribution in BOED. We compare this approach on SBI-based models in real-world simulators in epidemiology and biology, showing notable improvements in inference.

Stochastic Gradient Bayesian Optimal Experimental Designs for Simulation-based Inference

Simulation-based inference (SBI) methods tackle complex scientific models with challenging inverse problems. However, SBI models often face a significant hurdle due to their non-differentiable nature, which hampers the use of gradient-based optimization techniques. Bayesian Optimal Experimental Design (BOED) is a powerful approach that aims to make the most efficient use of experimental resources for improved inferences. While stochastic gradient BOED methods have shown promising results in high-dimensional design problems, they have mostly neglected the integration of BOED with SBI due to the difficult non-differentiable property of many SBI simulators. In this work, we establish a crucial connection between ratio-based SBI inference algorithms and stochastic gradient-based variational inference by leveraging mutual information bounds. This connection allows us to extend BOED to SBI applications, enabling the simultaneous optimization of experimental designs and amortized inference functions. We demonstrate our approach on a simple linear model and offer implementation details for practitioners.

An Optimal Likelihood Free Method for Biological Model Selection

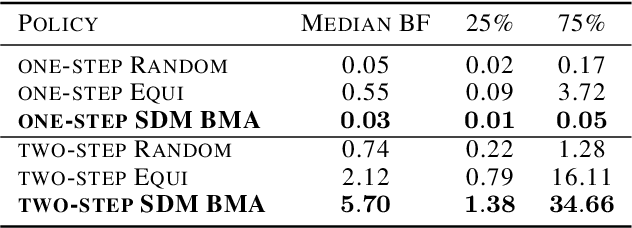
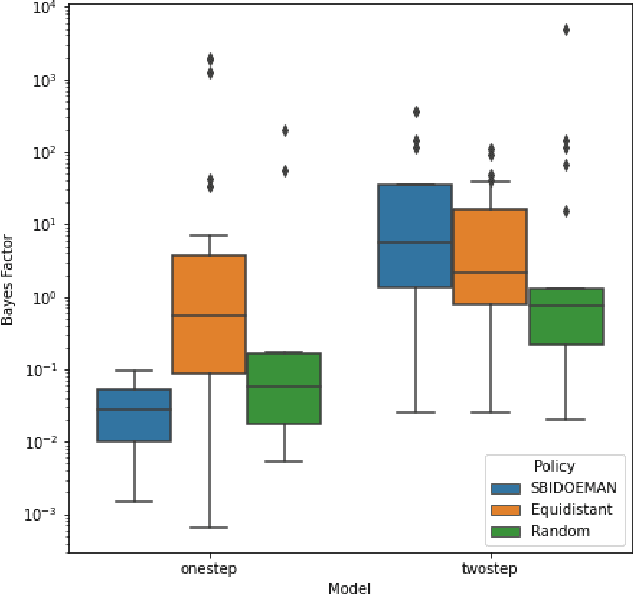
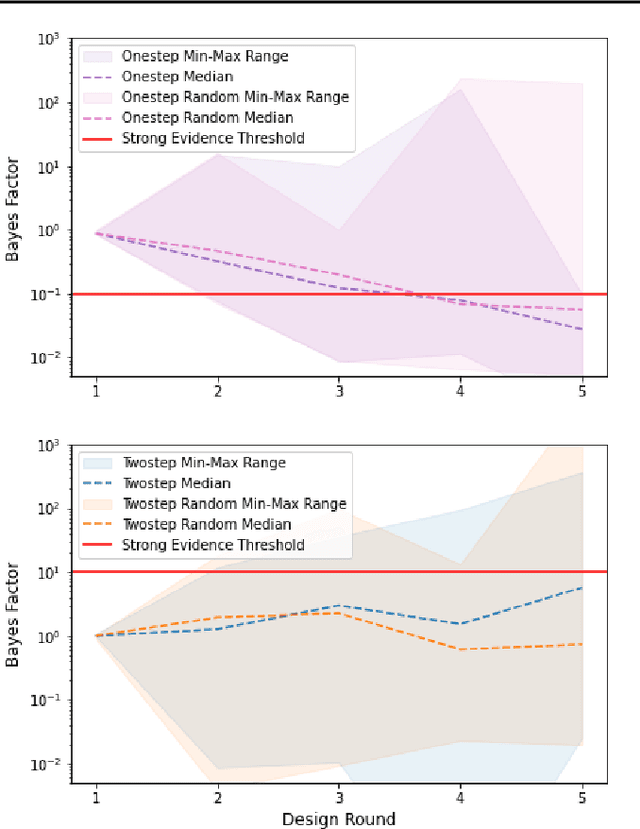
Systems biology seeks to create math models of biological systems to reduce inherent biological complexity and provide predictions for applications such as therapeutic development. However, it remains a challenge to determine which math model is correct and how to arrive optimally at the answer. We present an algorithm for automated biological model selection using mathematical models of systems biology and likelihood free inference methods. Our algorithm shows improved performance in arriving at correct models without a priori information over conventional heuristics used in experimental biology and random search. This method shows promise to accelerate biological basic science and drug discovery.