Synthesising a Database of Parameterised Linear and Non-Linear Invariants for Time-Series Constraints

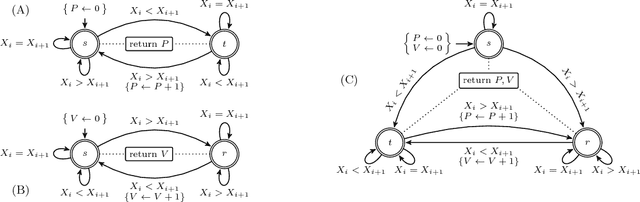
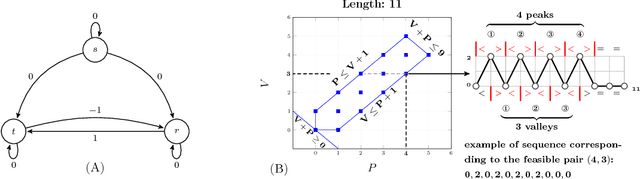
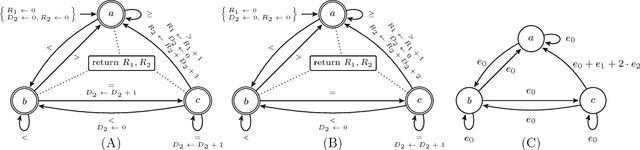
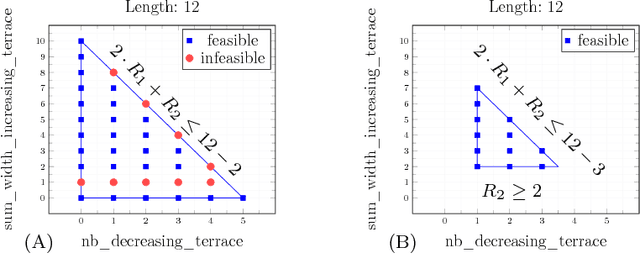
Many constraints restricting the result of some computations over an integer sequence can be compactly represented by register automata. We improve the propagation of the conjunction of such constraints on the same sequence by synthesising a database of linear and non-linear invariants using their register-automaton representation. The obtained invariants are formulae parameterised by a function of the sequence length and proven to be true for any long enough sequence. To assess the quality of such linear invariants, we developed a method to verify whether a generated linear invariant is a facet of the convex hull of the feasible points. This method, as well as the proof of non-linear invariants, are based on the systematic generation of constant-size deterministic finite automata that accept all integer sequences whose result verifies some simple condition. We apply such methodology to a set of 44 time-series constraints and obtain 1400 linear invariants from which 70% are facet defining, and 600 non-linear invariants, which were tested on short-term electricity production problems.

Global Constraint Catalog, Volume II, Time-Series Constraints

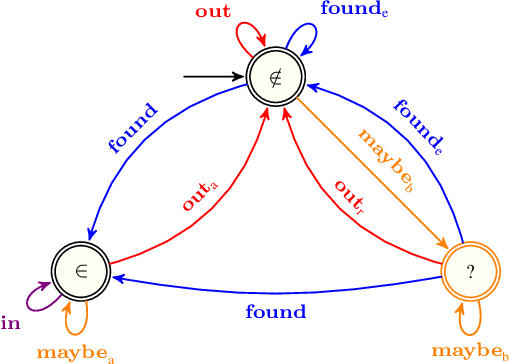
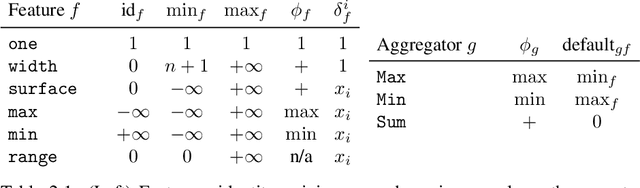
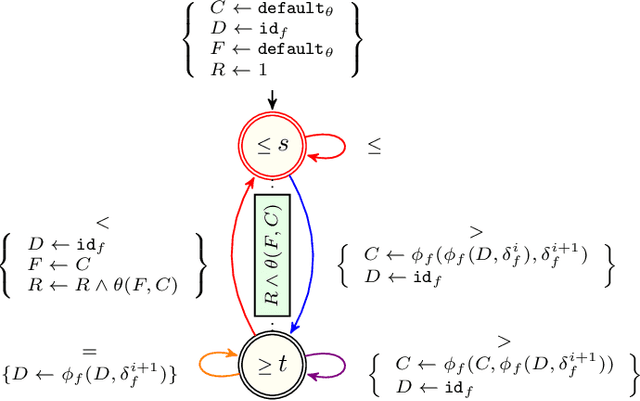
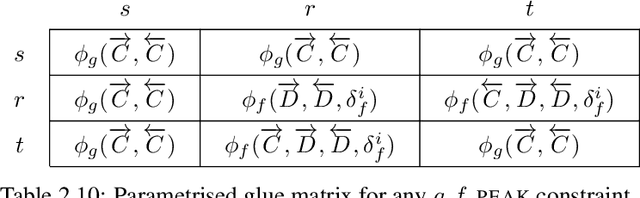
First this report presents a restricted set of finite transducers used to synthesise structural time-series constraints described by means of a multi-layered function composition scheme. Second it provides the corresponding synthesised catalogue of structural time-series constraints where each constraint is explicitly described in terms of automata with registers.