Classification and clustering for observations of event time data using non-homogeneous Poisson process models

Data of the form of event times arise in various applications. A simple model for such data is a non-homogeneous Poisson process (NHPP) which is specified by a rate function that depends on time. We consider the problem of having access to multiple independent observations of event time data, observed on a common interval, from which we wish to classify or cluster the observations according to their rate functions. Each rate function is unknown but assumed to belong to a finite number of rate functions each defining a distinct class. We model the rate functions using a spline basis expansion, the coefficients of which need to be estimated from data. The classification approach consists of using training data for which the class membership is known, to calculate maximum likelihood estimates of the coefficients for each group, then assigning test observations to a group by a maximum likelihood criterion. For clustering, by analogy to the Gaussian mixture model approach for Euclidean data, we consider mixtures of NHPP and use the expectation-maximisation algorithm to estimate the coefficients of the rate functions for the component models and group membership probabilities for each observation. The classification and clustering approaches perform well on both synthetic and real-world data sets. Code associated with this paper is available at https://github.com/duncan-barrack/NHPP .

AMP: a new time-frequency feature extraction method for intermittent time-series data

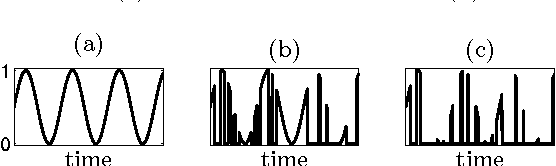
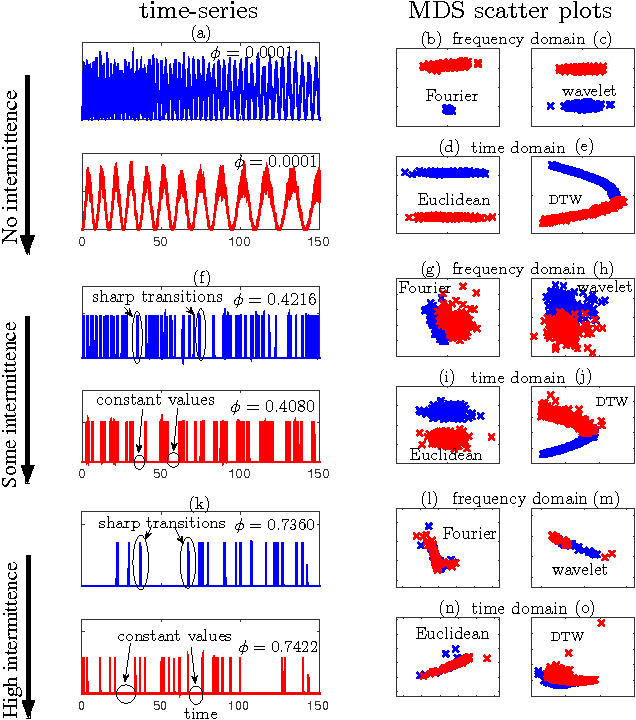
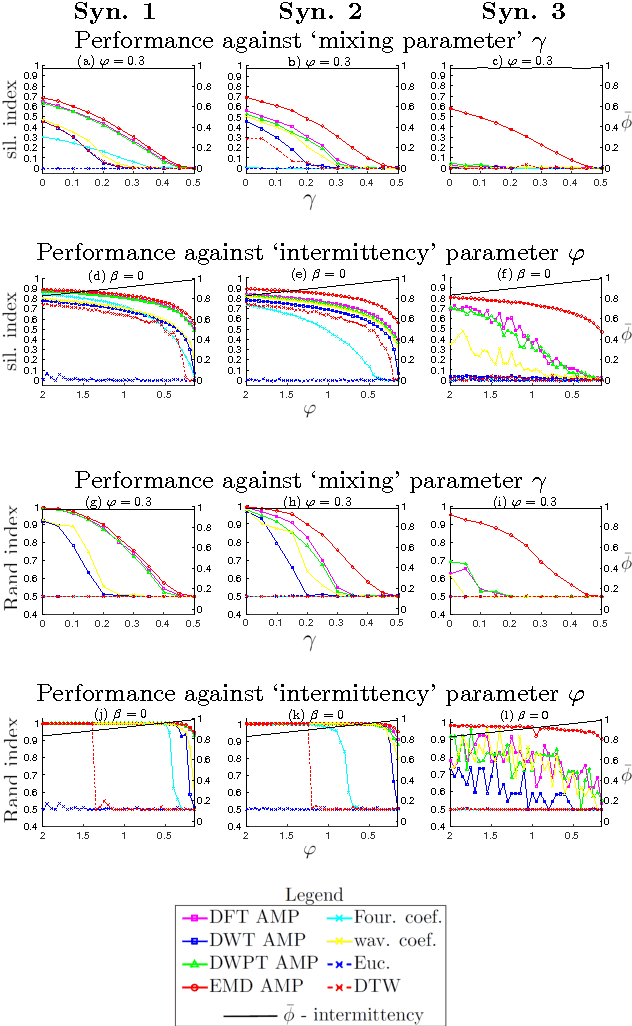
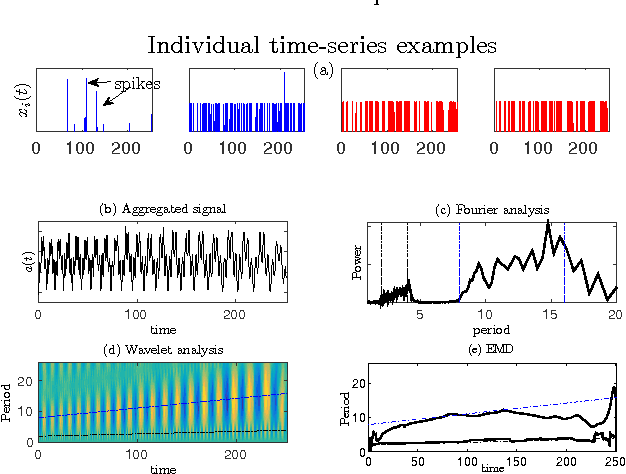
The characterisation of time-series data via their most salient features is extremely important in a range of machine learning task, not least of all with regards to classification and clustering. While there exist many feature extraction techniques suitable for non-intermittent time-series data, these approaches are not always appropriate for intermittent time-series data, where intermittency is characterized by constant values for large periods of time punctuated by sharp and transient increases or decreases in value. Motivated by this, we present aggregation, mode decomposition and projection (AMP) a feature extraction technique particularly suited to intermittent time-series data which contain time-frequency patterns. For our method all individual time-series within a set are combined to form a non-intermittent aggregate. This is decomposed into a set of components which represent the intrinsic time-frequency signals within the data set. Individual time-series can then be fit to these components to obtain a set of numerical features that represent their intrinsic time-frequency patterns. To demonstrate the effectiveness of AMP, we evaluate against the real word task of clustering intermittent time-series data. Using synthetically generated data we show that a clustering approach which uses the features derived from AMP significantly outperforms traditional clustering methods. Our technique is further exemplified on a real world data set where AMP can be used to discover groupings of individuals which correspond to real world sub-populations.