Exactly or Approximately Wasserstein Distributionally Robust Estimation According to Wasserstein Radii Being Small or Large

This paper primarily considers the robust estimation problem under Wasserstein distance constraints on the parameter and noise distributions in the linear measurement model with additive noise, which can be formulated as an infinite-dimensional nonconvex minimax problem. We prove that the existence of a saddle point for this problem is equivalent to that for a finite-dimensional minimax problem, and give a counterexample demonstrating that the saddle point may not exist. Motivated by this observation, we present a verifiable necessary and sufficient condition whose parameters can be derived from a convex problem and its dual. Additionally, we also introduce a simplified sufficient condition, which intuitively indicates that when the Wasserstein radii are small enough, the saddle point always exists. In the absence of the saddle point, we solve an finite-dimensional nonconvex minimax problem, obtained by restricting the estimator to be linear. Its optimal value establishes an upper bound on the robust estimation problem, while its optimal solution yields a robust linear estimator. Numerical experiments are also provided to validate our theoretical results.

A sparse semismooth Newton based augmented Lagrangian method for large-scale support vector machines

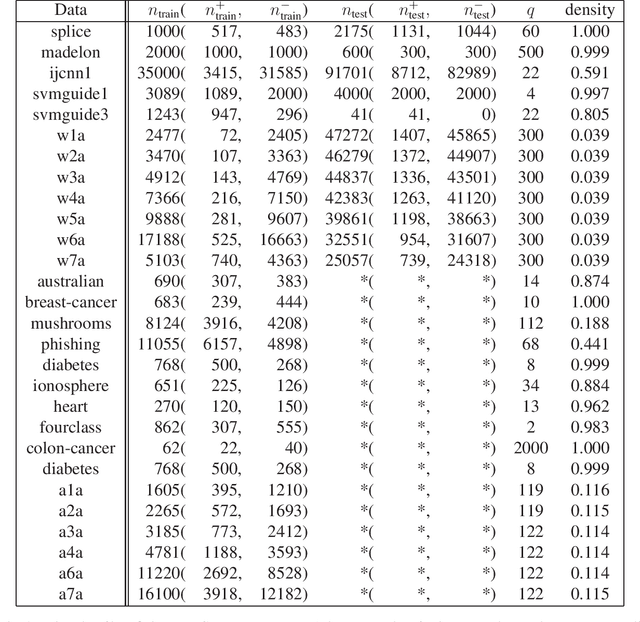
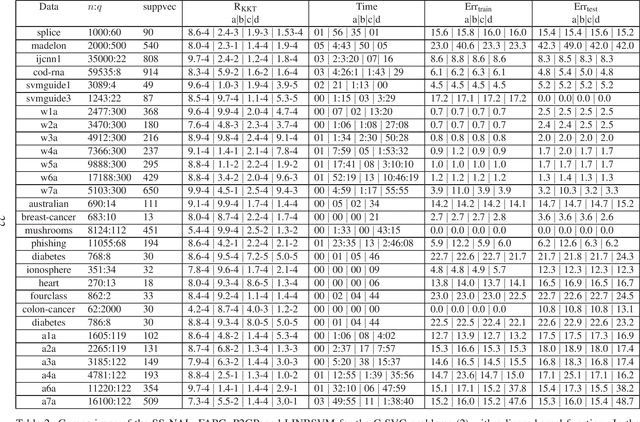
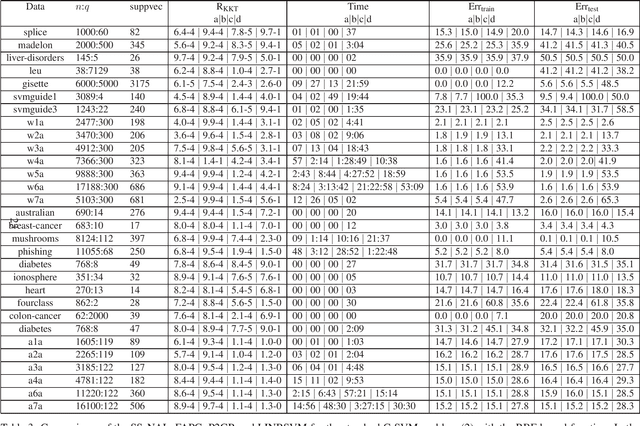
Support vector machines (SVMs) are successful modeling and prediction tools with a variety of applications. Previous work has demonstrated the superiority of the SVMs in dealing with the high dimensional, low sample size problems. However, the numerical difficulties of the SVMs will become severe with the increase of the sample size. Although there exist many solvers for the SVMs, only few of them are designed by exploiting the special structures of the SVMs. In this paper, we propose a highly efficient sparse semismooth Newton based augmented Lagrangian method for solving a large-scale convex quadratic programming problem with a linear equality constraint and a simple box constraint, which is generated from the dual problems of the SVMs. By leveraging the primal-dual error bound result, the fast local convergence rate of the augmented Lagrangian method can be guaranteed. Furthermore, by exploiting the second-order sparsity of the problem when using the semismooth Newton method, the algorithm can efficiently solve the aforementioned difficult problems. Finally, numerical comparisons demonstrate that the proposed algorithm outperforms the current state-of-the-art solvers for the large-scale SVMs.