Dror Freirich
Characterization of the Distortion-Perception Tradeoff for Finite Channels with Arbitrary Metrics
Feb 03, 2024

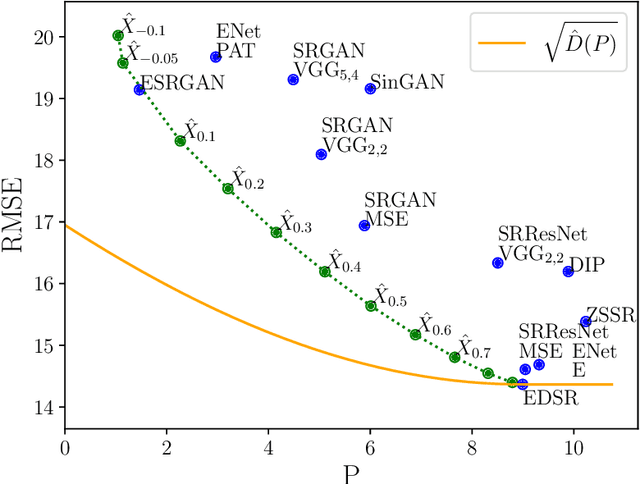
Abstract:Whenever inspected by humans, reconstructed signals should not be distinguished from real ones. Typically, such a high perceptual quality comes at the price of high reconstruction error, and vice versa. We study this distortion-perception (DP) tradeoff over finite-alphabet channels, for the Wasserstein-$1$ distance induced by a general metric as the perception index, and an arbitrary distortion matrix. Under this setting, we show that computing the DP function and the optimal reconstructions is equivalent to solving a set of linear programming problems. We provide a structural characterization of the DP tradeoff, where the DP function is piecewise linear in the perception index. We further derive a closed-form expression for the case of binary sources.
Perceptual Kalman Filters: Online State Estimation under a Perfect Perceptual-Quality Constraint
Jun 04, 2023



Abstract:Many practical settings call for the reconstruction of temporal signals from corrupted or missing data. Classic examples include decoding, tracking, signal enhancement and denoising. Since the reconstructed signals are ultimately viewed by humans, it is desirable to achieve reconstructions that are pleasing to human perception. Mathematically, perfect perceptual-quality is achieved when the distribution of restored signals is the same as that of natural signals, a requirement which has been heavily researched in static estimation settings (i.e. when a whole signal is processed at once). Here, we study the problem of optimal causal filtering under a perfect perceptual-quality constraint, which is a task of fundamentally different nature. Specifically, we analyze a Gaussian Markov signal observed through a linear noisy transformation. In the absence of perceptual constraints, the Kalman filter is known to be optimal in the MSE sense for this setting. Here, we show that adding the perfect perceptual quality constraint (i.e. the requirement of temporal consistency), introduces a fundamental dilemma whereby the filter may have to "knowingly" ignore new information revealed by the observations in order to conform to its past decisions. This often comes at the cost of a significant increase in the MSE (beyond that encountered in static settings). Our analysis goes beyond the classic innovation process of the Kalman filter, and introduces the novel concept of an unutilized information process. Using this tool, we present a recursive formula for perceptual filters, and demonstrate the qualitative effects of perfect perceptual-quality estimation on a video reconstruction problem.
A Theory of the Distortion-Perception Tradeoff in Wasserstein Space
Jul 06, 2021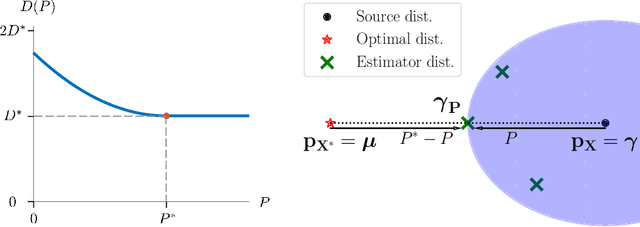


Abstract:The lower the distortion of an estimator, the more the distribution of its outputs generally deviates from the distribution of the signals it attempts to estimate. This phenomenon, known as the perception-distortion tradeoff, has captured significant attention in image restoration, where it implies that fidelity to ground truth images comes at the expense of perceptual quality (deviation from statistics of natural images). However, despite the increasing popularity of performing comparisons on the perception-distortion plane, there remains an important open question: what is the minimal distortion that can be achieved under a given perception constraint? In this paper, we derive a closed form expression for this distortion-perception (DP) function for the mean squared-error (MSE) distortion and the Wasserstein-2 perception index. We prove that the DP function is always quadratic, regardless of the underlying distribution. This stems from the fact that estimators on the DP curve form a geodesic in Wasserstein space. In the Gaussian setting, we further provide a closed form expression for such estimators. For general distributions, we show how these estimators can be constructed from the estimators at the two extremes of the tradeoff: The global MSE minimizer, and a minimizer of the MSE under a perfect perceptual quality constraint. The latter can be obtained as a stochastic transformation of the former.
Distributional Multivariate Policy Evaluation and Exploration with the Bellman GAN
Aug 06, 2018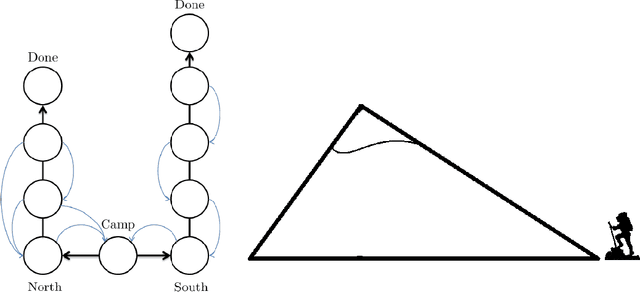
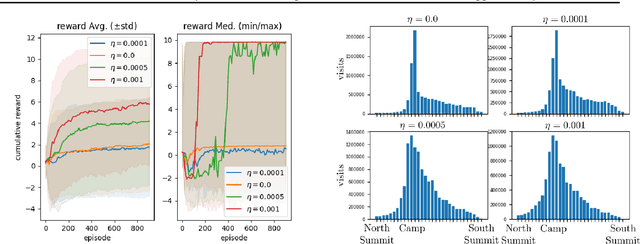
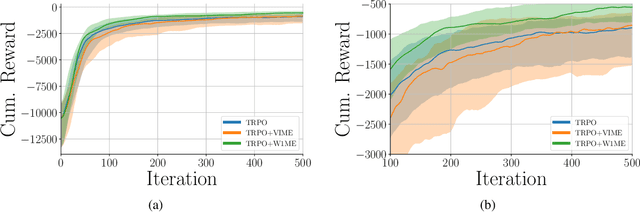
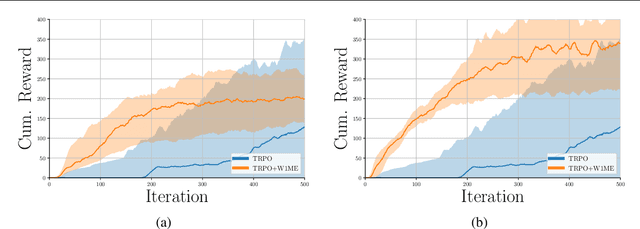
Abstract:The recently proposed distributional approach to reinforcement learning (DiRL) is centered on learning the distribution of the reward-to-go, often referred to as the value distribution. In this work, we show that the distributional Bellman equation, which drives DiRL methods, is equivalent to a generative adversarial network (GAN) model. In this formulation, DiRL can be seen as learning a deep generative model of the value distribution, driven by the discrepancy between the distribution of the current value, and the distribution of the sum of current reward and next value. We use this insight to propose a GAN-based approach to DiRL, which leverages the strengths of GANs in learning distributions of high-dimensional data. In particular, we show that our GAN approach can be used for DiRL with multivariate rewards, an important setting which cannot be tackled with prior methods. The multivariate setting also allows us to unify learning the distribution of values and state transitions, and we exploit this idea to devise a novel exploration method that is driven by the discrepancy in estimating both values and states.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge