Adaptive Sampling for Linear Sensing Systems via Langevin Dynamics

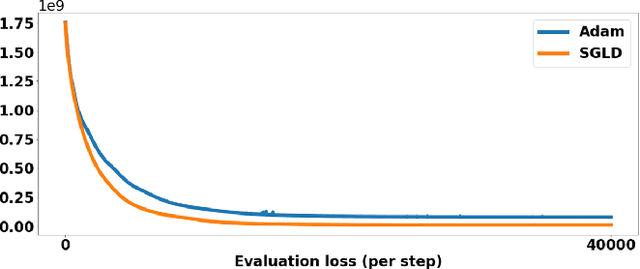
Adaptive or dynamic signal sampling in sensing systems can adapt subsequent sampling strategies based on acquired signals, thereby potentially improving image quality and speed. This paper proposes a Bayesian method for adaptive sampling based on greedy variance reduction and stochastic gradient Langevin dynamics (SGLD). The image priors involved can be either analytical or neural network-based. Notably, the learned image priors generalize well to out-of-distribution test cases that have different statistics than the training dataset. As a real-world validation, the method is applied to accelerate the acquisition of magnetic resonance imaging (MRI). Compared to non-adaptive sampling, the proposed method effectively improved the image quality by 2-3 dB in PSNR, and improved the restoration of subtle details.

Stochastic Optimization of 3D Non-Cartesian Sampling Trajectory (SNOPY)

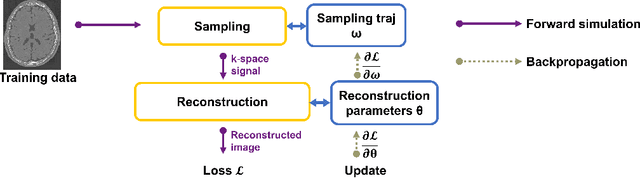
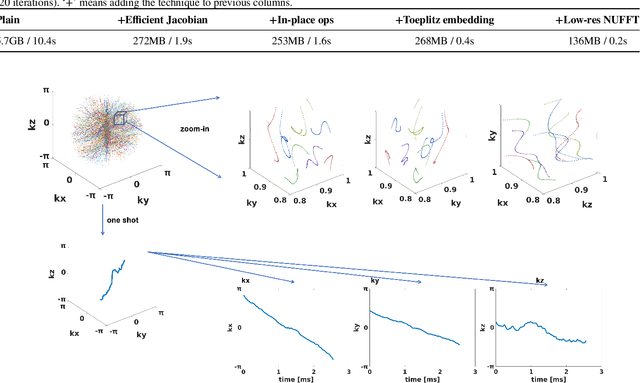
Optimizing 3D k-space sampling trajectories for efficient MRI is important yet challenging. This work proposes a generalized framework for optimizing 3D non-Cartesian sampling patterns via data-driven optimization. We built a differentiable MRI system model to enable gradient-based methods for sampling trajectory optimization. By combining training losses, the algorithm can simultaneously optimize multiple properties of sampling patterns, including image quality, hardware constraints (maximum slew rate and gradient strength), reduced peripheral nerve stimulation (PNS), and parameter-weighted contrast. The proposed method can either optimize the gradient waveform (spline-based freeform optimization) or optimize properties of given sampling trajectories (such as the rotation angle of radial trajectories). Notably, the method optimizes sampling trajectories synergistically with either model-based or learning-based reconstruction methods. We proposed several strategies to alleviate the severe non-convexity and huge computation demand posed by the high-dimensional optimization. The corresponding code is organized as an open-source, easy-to-use toolbox. We applied the optimized trajectory to multiple applications including structural and functional imaging. In the simulation studies, the reconstruction PSNR of a 3D kooshball trajectory was increased by 4 dB with SNOPY optimization. In the prospective studies, by optimizing the rotation angles of a stack-of-stars (SOS) trajectory, SNOPY improved the PSNR by 1.4dB compared to the best empirical method. Optimizing the gradient waveform of a rotational EPI trajectory improved subjects' rating of the PNS effect from 'strong' to 'mild.' In short, SNOPY provides an efficient data-driven and optimization-based method to tailor non-Cartesian sampling trajectories.

Off-resonance artifact correction for magnetic resonance imaging: a review

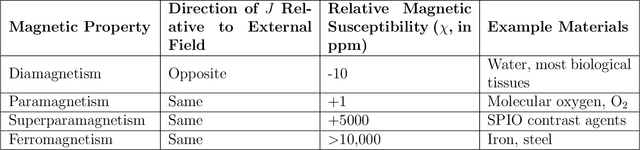
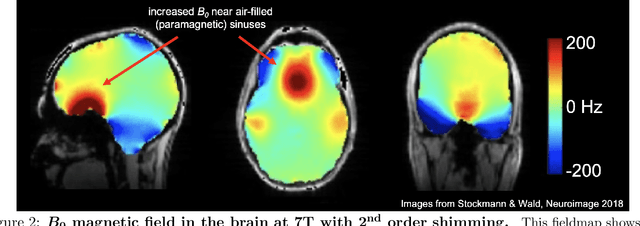
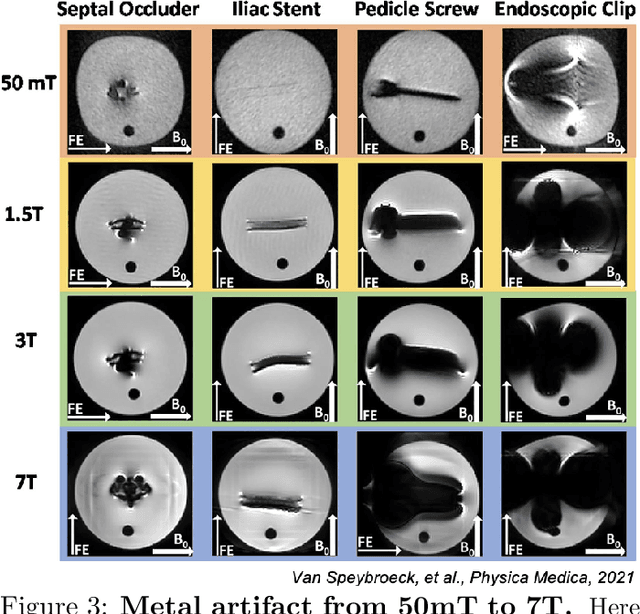
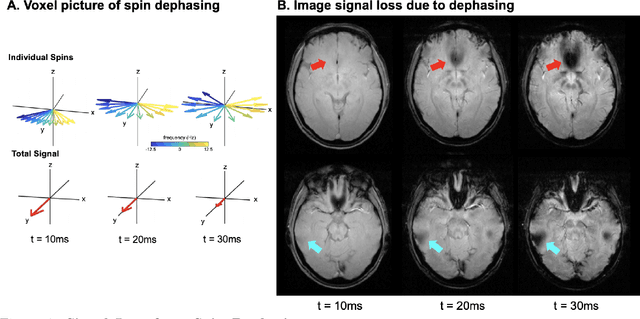
In magnetic resonance imaging (MRI), inhomogeneity in the main magnetic field used for imaging, referred to as off-resonance, can lead to image artifacts ranging from mild to severe depending on the application. Off-resonance artifacts, such as signal loss, geometric distortions, and blurring, can compromise the clinical and scientific utility of MR images. In this review, we describe sources of off-resonance in MRI, how off-resonance affects images, and strategies to prevent and correct for off-resonance. Given recent advances and the great potential of low field and/or portable MRI, we also highlight the advantages and challenges of imaging at low field with respect to off-resonance.

Manifold Model for High-Resolution fMRI Joint Reconstruction and Dynamic Quantification

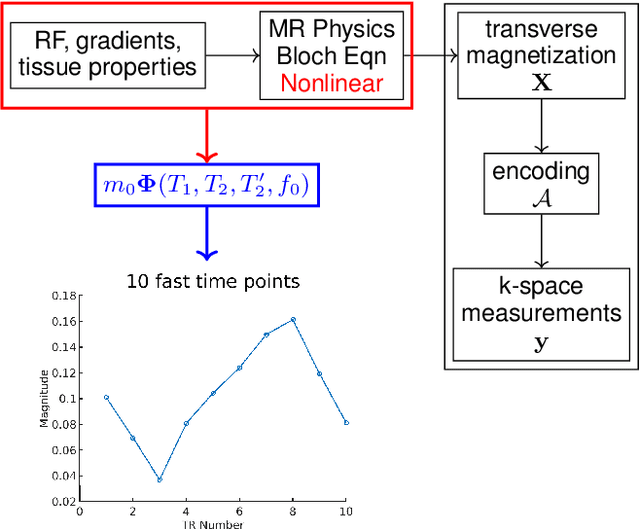
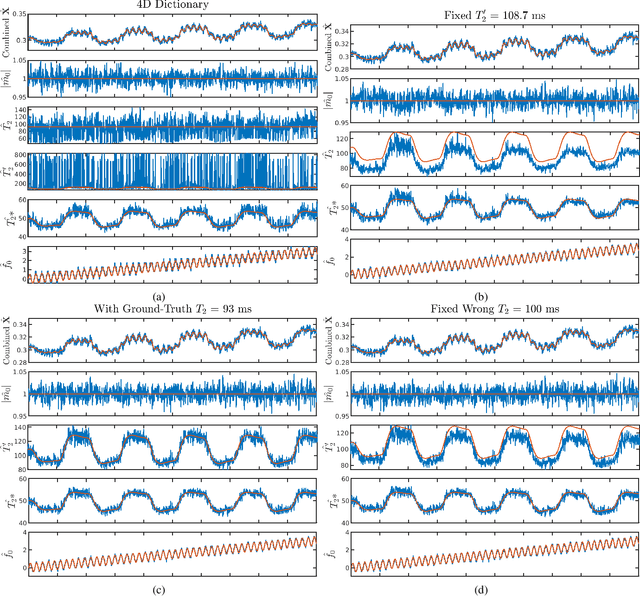
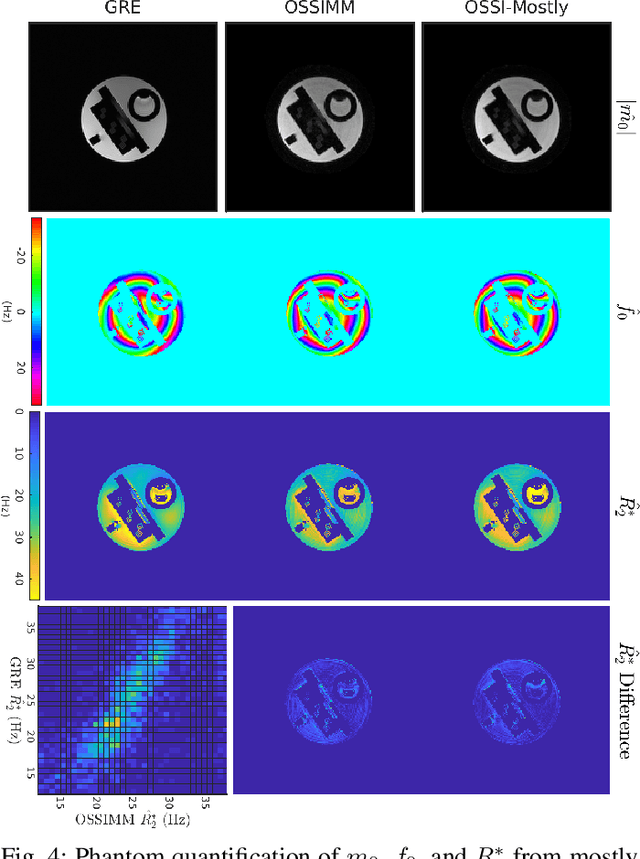
Oscillating Steady-State Imaging (OSSI) is a recent fMRI acquisition method that exploits a large and oscillating signal, and can provide high SNR fMRI. However, the oscillatory nature of the signal leads to an increased number of acquisitions. To improve temporal resolution and accurately model the nonlinearity of OSSI signals, we build the MR physics for OSSI signal generation as a regularizer for the undersampled reconstruction rather than using subspace models that are not well suited for the data. Our proposed physics-based manifold model turns the disadvantages of OSSI acquisition into advantages and enables joint reconstruction and quantification. OSSI manifold model (OSSIMM) outperforms subspace models and reconstructs high-resolution fMRI images with a factor of 12 acceleration and without spatial or temporal resolution smoothing. Furthermore, OSSIMM can dynamically quantify important physics parameters, including $R_2^*$ maps, with a temporal resolution of 150 ms.

B-spline Parameterized Joint Optimization of Reconstruction and K-space Trajectories (BJORK) for Accelerated 2D MRI

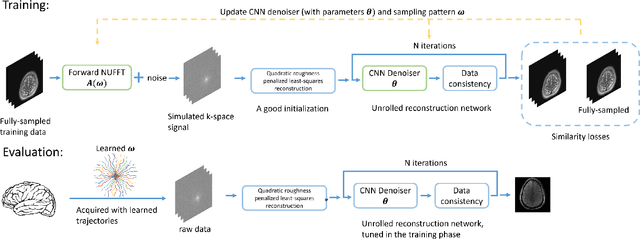
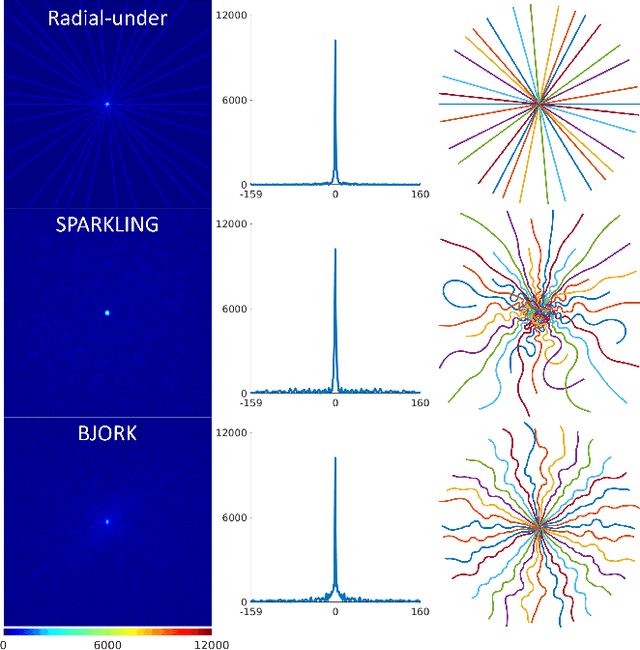
Optimizing k-space sampling trajectories is a challenging topic for fast magnetic resonance imaging (MRI). This work proposes to optimize a reconstruction algorithm and sampling trajectories jointly concerning image reconstruction quality. We parameterize trajectories with quadratic B-spline kernels to reduce the number of parameters and enable multi-scale optimization, which may help to avoid sub-optimal local minima. The algorithm includes an efficient non-Cartesian unrolled neural network-based reconstruction and an accurate approximation for backpropagation through the non-uniform fast Fourier transform (NUFFT) operator to accurately reconstruct and back-propagate multi-coil non-Cartesian data. Penalties on slew rate and gradient amplitude enforce hardware constraints. Sampling and reconstruction are trained jointly using large public datasets. To correct the potential eddy-current effect introduced by the curved trajectory, we use a pencil-beam trajectory mapping technique. In both simulations and in-vivo experiments, the learned trajectory demonstrates significantly improved image quality compared to previous model-based and learning-based trajectory optimization methods for 20x acceleration factors. Though trained with neural network-based reconstruction, the proposed trajectory also leads to improved image quality with compressed sensing-based reconstruction.