Minimax Rates of Estimation for Optimal Transport Map between Infinite-Dimensional Spaces

We investigate the estimation of an optimal transport map between probability measures on an infinite-dimensional space and reveal its minimax optimal rate. Optimal transport theory defines distances within a space of probability measures, utilizing an optimal transport map as its key component. Estimating the optimal transport map from samples finds several applications, such as simulating dynamics between probability measures and functional data analysis. However, some transport maps on infinite-dimensional spaces require exponential-order data for estimation, which undermines their applicability. In this paper, we investigate the estimation of an optimal transport map between infinite-dimensional spaces, focusing on optimal transport maps characterized by the notion of $\gamma$-smoothness. Consequently, we show that the order of the minimax risk is polynomial rate in the sample size even in the infinite-dimensional setup. We also develop an estimator whose estimation error matches the minimax optimal rate. With these results, we obtain a class of reasonably estimable optimal transport maps on infinite-dimensional spaces and a method for their estimation. Our experiments validate the theory and practical utility of our approach with application to functional data analysis.

coverforest: Conformal Predictions with Random Forest in Python

Conformal prediction provides a framework for uncertainty quantification, specifically in the forms of prediction intervals and sets with distribution-free guaranteed coverage. While recent cross-conformal techniques such as CV+ and Jackknife+-after-bootstrap achieve better data efficiency than traditional split conformal methods, they incur substantial computational costs due to required pairwise comparisons between training and test samples' out-of-bag scores. Observing that these methods naturally extend from ensemble models, particularly random forests, we leverage existing optimized random forest implementations to enable efficient cross-conformal predictions. We present coverforest, a Python package that implements efficient conformal prediction methods specifically optimized for random forests. coverforest supports both regression and classification tasks through various conformal prediction methods, including split conformal, CV+, Jackknife+-after-bootstrap, and adaptive prediction sets. Our package leverages parallel computing and Cython optimizations to speed up out-of-bag calculations. Our experiments demonstrate that coverforest's predictions achieve the desired level of coverage. In addition, its training and prediction times can be faster than an existing implementation by 2--9 times. The source code for the coverforest is hosted on GitHub at https://github.com/donlapark/coverforest.

Investigating Privacy Leakage in Dimensionality Reduction Methods via Reconstruction Attack

This study investigates privacy leakage in dimensionality reduction methods through a novel machine learning-based reconstruction attack. Employing an \emph{informed adversary} threat model, we develop a neural network capable of reconstructing high-dimensional data from low-dimensional embeddings. We evaluate six popular dimensionality reduction techniques: PCA, sparse random projection (SRP), multidimensional scaling (MDS), Isomap, $t$-SNE, and UMAP. Using both MNIST and NIH Chest X-ray datasets, we perform a qualitative analysis to identify key factors affecting reconstruction quality. Furthermore, we assess the effectiveness of an additive noise mechanism in mitigating these reconstruction attacks.

An Explainable Machine Learning Approach to Visual-Interactive Labeling: A Case Study on Non-communicable Disease Data

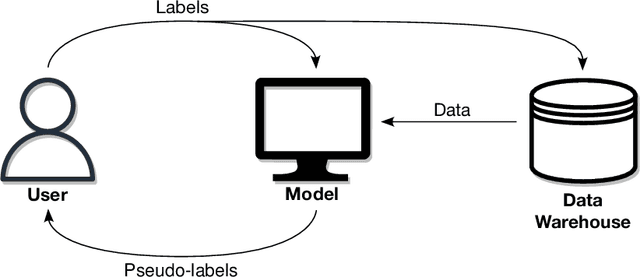
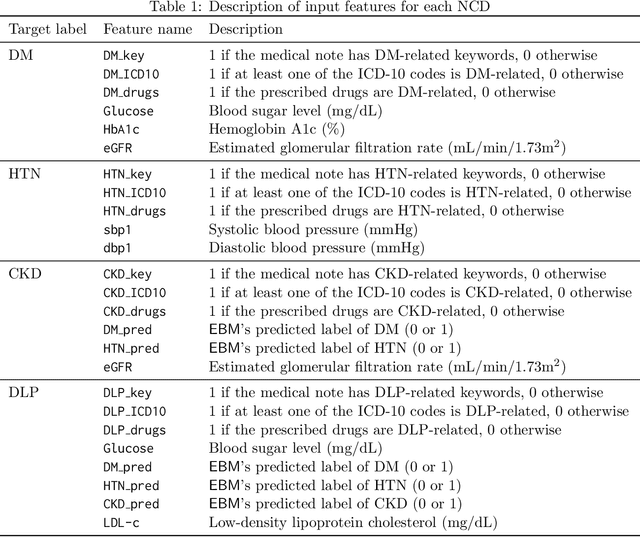
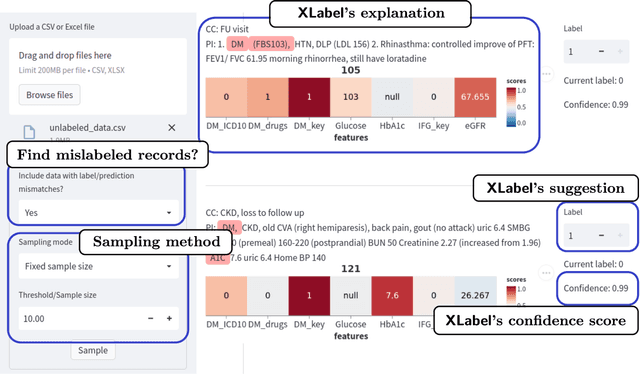
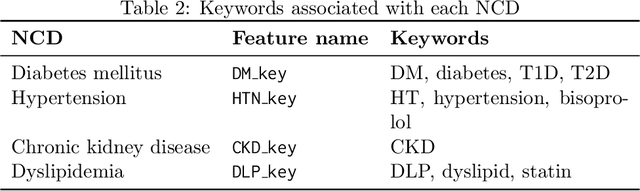
We introduce a new visual-interactive tool: Explainable Labeling Assistant (XLabel) that takes an explainable machine learning approach to data labeling. The main component of XLabel is the Explainable Boosting Machine (EBM), a predictive model that can calculate the contribution of each input feature towards the final prediction. As a case study, we use XLabel to predict the labels of four non-communicable diseases (NCDs): diabetes, hypertension, chronic kidney disease, and dyslipidemia. We demonstrate that EBM is an excellent choice of predictive model by comparing it against a rule-based and four other machine learning models. By performing 5-fold cross-validation on 427 medical records, EBM's prediction accuracy, precision, and F1-score are greater than 0.95 in all four NCDs. It performed as well as two black-box models and outperformed the other models in these metrics. In an additional experiment, when 40% of the records were intentionally mislabeled, EBM could recall the correct labels of more than 90% of these records.

Differential Privacy of Dirichlet Posterior Sampling

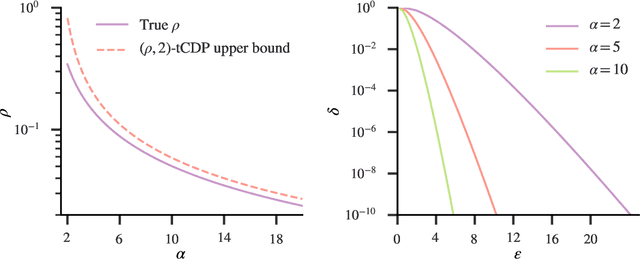
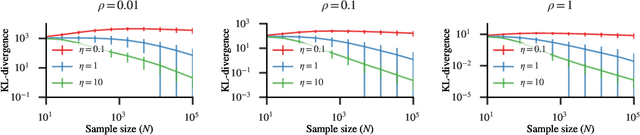
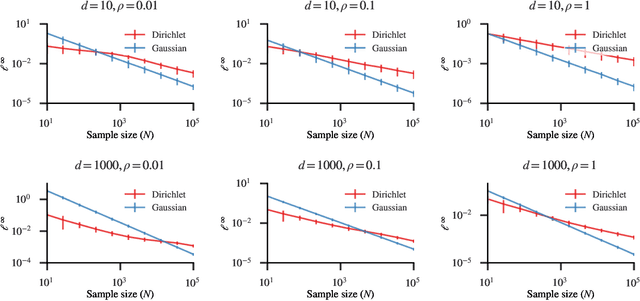
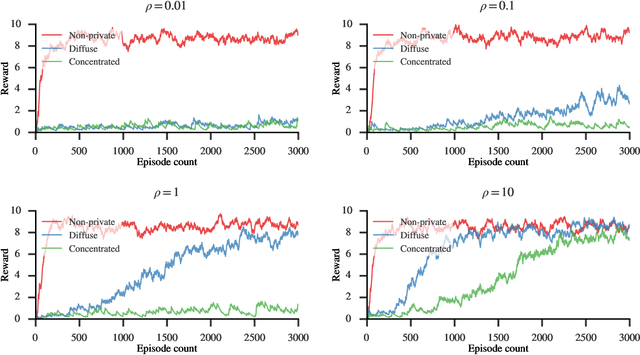
Besides the Laplace distribution and the Gaussian distribution, there are many more probability distributions which is not well-understood in terms of privacy-preserving property of a random draw -- one of which is the Dirichlet distribution. In this work, we study the inherent privacy of releasing a single draw from a Dirichlet posterior distribution. As a complement to the previous study that provides general theories on the differential privacy of posterior sampling from exponential families, this study focuses specifically on the Dirichlet posterior sampling and its privacy guarantees. With the notion of truncated concentrated differential privacy (tCDP), we are able to derive a simple privacy guarantee of the Dirichlet posterior sampling, which effectively allows us to analyze its utility in various settings. Specifically, we prove accuracy guarantees of private Multinomial-Dirichlet sampling, which is prevalent in Bayesian tasks, and private release of a normalized histogram. In addition, with our results, it is possible to make Bayesian reinforcement learning differentially private by modifying the Dirichlet sampling for state transition probabilities.

Short-term daily precipitation forecasting with seasonally-integrated autoencoder

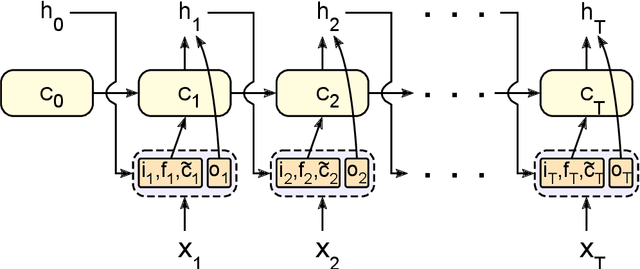
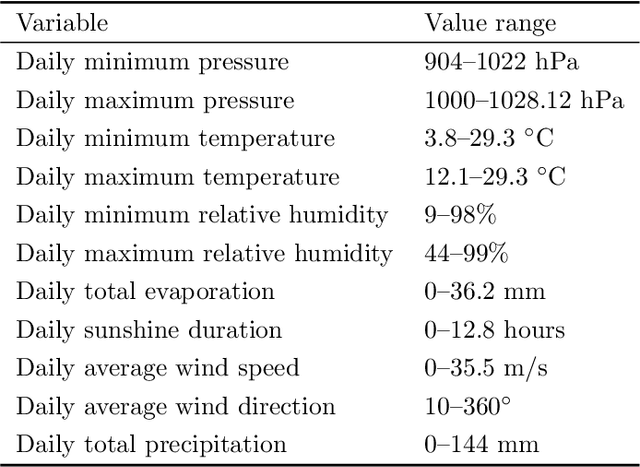
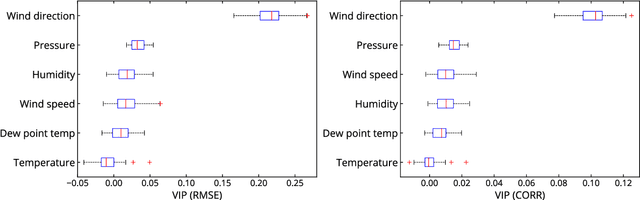
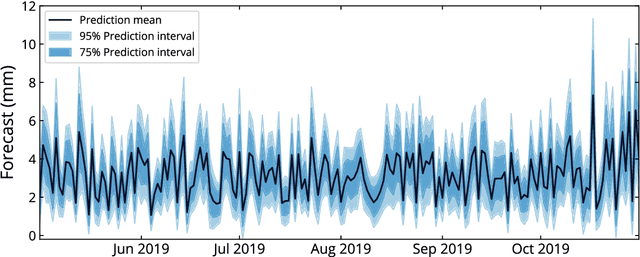
Short-term precipitation forecasting is essential for planning of human activities in multiple scales, ranging from individuals' planning, urban management to flood prevention. Yet the short-term atmospheric dynamics are highly nonlinear that it cannot be easily captured with classical time series models. On the other hand, deep learning models are good at learning nonlinear interactions, but they are not designed to deal with the seasonality in time series. In this study, we aim to develop a forecasting model that can both handle the nonlinearities and detect the seasonality hidden within the daily precipitation data. To this end, we propose a seasonally-integrated autoencoder (SSAE) consisting of two long short-term memory (LSTM) autoencoders: one for learning short-term dynamics, and the other for learning the seasonality in the time series. Our experimental results show that not only does the SSAE outperform various time series models regardless of the climate type, but it also has low output variance compared to other deep learning models. The results also show that the seasonal component of the SSAE helped improve the correlation between the forecast and the actual values from 4% at horizon 1 to 37% at horizon 3.

Universal consistency of Wasserstein $k$-NN classifier

The Wasserstein distance provides a notion of dissimilarities between probability measures, which has recent applications in learning of structured data with varying size such as images and text documents. In this work, we analyze the $k$-nearest neighbor classifier ($k$-NN) under the Wasserstein distance and establish the universal consistency on families of distributions. Using previous known results on the consistency of the $k$-NN classifier on infinite dimensional metric spaces, it suffices to show that the families is a countable union of finite dimensional components. As a result, we are able to prove universal consistency of $k$-NN on spaces of finitely supported measures, the space of finite wavelet series and the spaces of Gaussian measures with commuting covariance matrices.