A Robust Monotonic Single-Index Model for Skewed and Heavy-Tailed Data: A Deep Neural Network Approach Applied to Periodontal Studies

Periodontal pocket depth is a widely used biomarker for diagnosing risk of periodontal disease. However, pocket depth typically exhibits skewness and heavy-tailedness, and its relationship with clinical risk factors is often nonlinear. Motivated by periodontal studies, this paper develops a robust single-index modal regression framework for analyzing skewed and heavy-tailed data. Our method has the following novel features: (1) a flexible two-piece scale Student-$t$ error distribution that generalizes both normal and two-piece scale normal distributions; (2) a deep neural network with guaranteed monotonicity constraints to estimate the unknown single-index function; and (3) theoretical guarantees, including model identifiability and a universal approximation theorem. Our single-index model combines the flexibility of neural networks and the two-piece scale Student-$t$ distribution, delivering robust mode-based estimation that is resistant to outliers, while retaining clinical interpretability through parametric index coefficients. We demonstrate the performance of our method through simulation studies and an application to periodontal disease data from the HealthPartners Institute of Minnesota. The proposed methodology is implemented in the \textsf{R} package \href{https://doi.org/10.32614/CRAN.package.DNNSIM}{\textsc{DNNSIM}}.

Bayesian nonparametric multiway regression for clustered binomial data

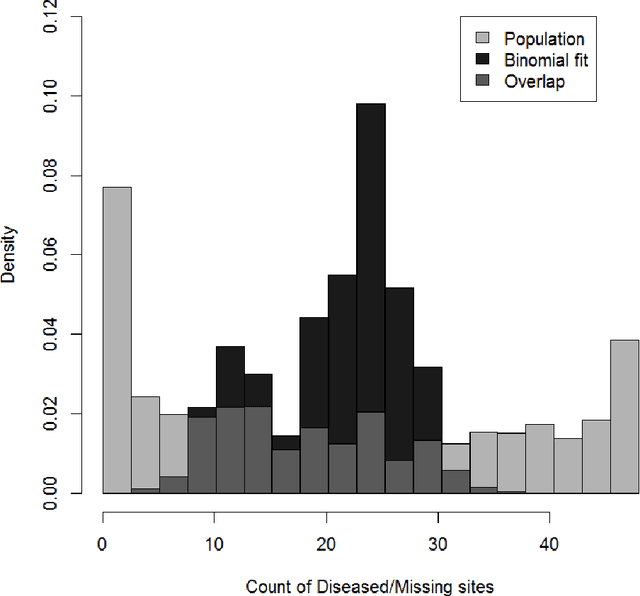
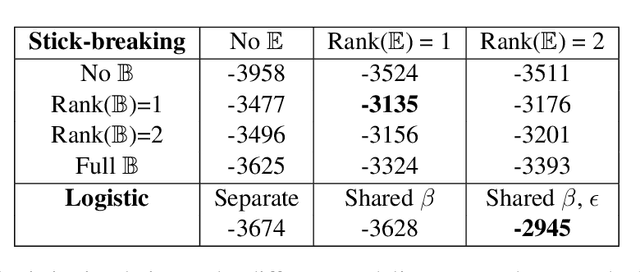
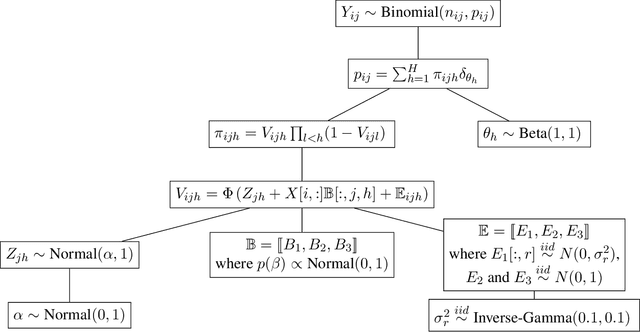
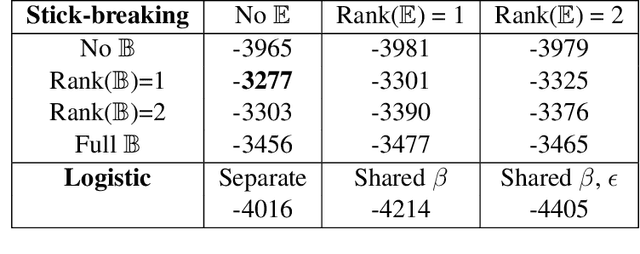
We introduce a Bayesian nonparametric regression model for data with multiway (tensor) structure, motivated by an application to periodontal disease (PD) data. Our outcome is the number of diseased sites measured over four different tooth types for each subject, with subject-specific covariates available as predictors. The outcomes are not well-characterized by simple parametric models, so we use a nonparametric approach with a binomial likelihood wherein the latent probabilities are drawn from a mixture with an arbitrary number of components, analogous to a Dirichlet Process (DP). We use a flexible probit stick-breaking formulation for the component weights that allows for covariate dependence and clustering structure in the outcomes. The parameter space for this model is large and multiway: patients $\times$ tooth types $\times$ covariates $\times$ components. We reduce its effective dimensionality, and account for the multiway structure, via low-rank assumptions. We illustrate how this can improve performance, and simplify interpretation, while still providing sufficient flexibility. We describe a general and efficient Gibbs sampling algorithm for posterior computation. The resulting fit to the PD data outperforms competitors, and is interpretable and well-calibrated. An interactive visual of the predictive model is available at http://ericfrazerlock.com/toothdata/ToothDisplay.html , and the code is available at https://github.com/lockEF/NonparametricMultiway .