Probabilistic quantile factor analysis

This paper extends quantile factor analysis to a probabilistic variant that incorporates regularization and computationally efficient variational approximations. By means of synthetic and real data experiments it is established that the proposed estimator can achieve, in many cases, better accuracy than a recently proposed loss-based estimator. We contribute to the literature on measuring uncertainty by extracting new indexes of low, medium and high economic policy uncertainty, using the probabilistic quantile factor methodology. Medium and high indexes have clear contractionary effects, while the low index is benign for the economy, showing that not all manifestations of uncertainty are the same.

High-dimensional macroeconomic forecasting using message passing algorithms

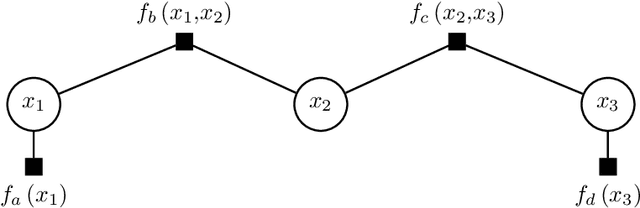
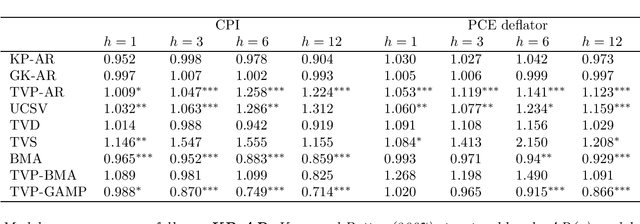
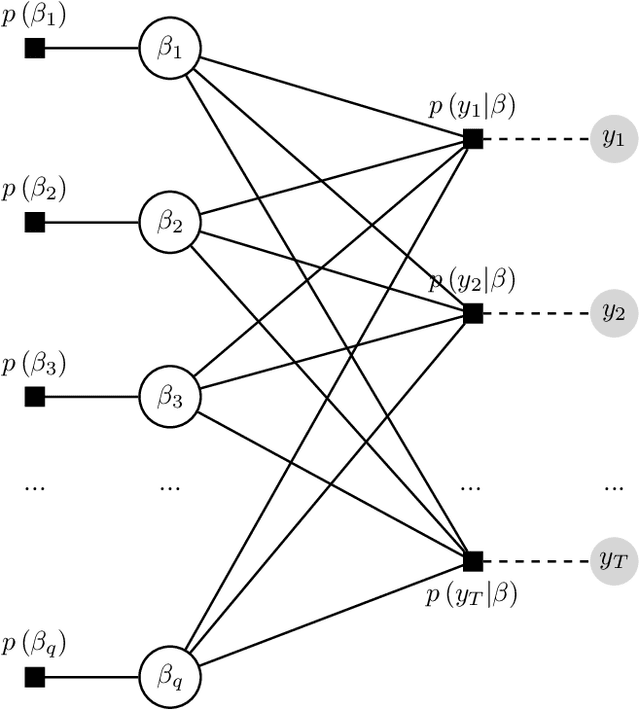
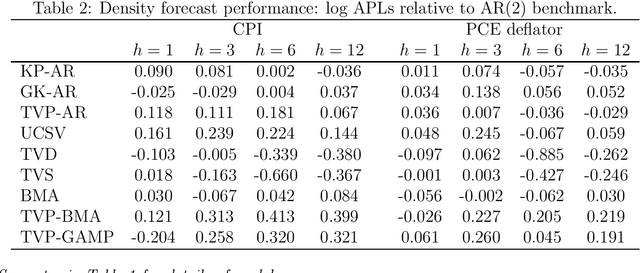
This paper proposes two distinct contributions to econometric analysis of large information sets and structural instabilities. First, it treats a regression model with time-varying coefficients, stochastic volatility and exogenous predictors, as an equivalent high-dimensional static regression problem with thousands of covariates. Inference in this specification proceeds using Bayesian hierarchical priors that shrink the high-dimensional vector of coefficients either towards zero or time-invariance. Second, it introduces the frameworks of factor graphs and message passing as a means of designing efficient Bayesian estimation algorithms. In particular, a Generalized Approximate Message Passing (GAMP) algorithm is derived that has low algorithmic complexity and is trivially parallelizable. The result is a comprehensive methodology that can be used to estimate time-varying parameter regressions with arbitrarily large number of exogenous predictors. In a forecasting exercise for U.S. price inflation this methodology is shown to work very well.