An Information-Minimal Geometry for Qubit-Efficient Optimization

Qubit-efficient optimization seeks to represent an $N$-variable combinatorial problem within a Hilbert space smaller than $2^N$, using only as much quantum structure as the objective itself requires. Quadratic unconstrained binary optimization (QUBO) problems, for example, depend only on pairwise information -- expectations and correlations between binary variables -- yet standard quantum circuits explore exponentially large state spaces. We recast qubit-efficient optimization as a geometry problem: the minimal representation should match the $O(N^2)$ structure of quadratic objectives. The key insight is that the local-consistency problem -- ensuring that pairwise marginals correspond to a realizable global distribution -- coincides exactly with the Sherali-Adams level-2 polytope $\mathrm{SA}(2)$, the tightest convex relaxation expressible at the two-body level. Previous qubit-efficient approaches enforced this consistency only implicitly. Here we make it explicit: (a) anchoring learning to the $\mathrm{SA}(2)$ geometry, (b) projecting via a differentiable iterative-proportional-fitting (IPF) step, and (c) decoding through a maximum-entropy Gibbs sampler. This yields a logarithmic-width pipeline ($2\lceil\log_2 N\rceil + 2$ qubits) that is classically simulable yet achieves strong empirical performance. On Gset Max-Cut instances (N=800--2000), depth-2--3 circuits reach near-optimal ratios ($r^* \approx 0.99$), surpassing direct $\mathrm{SA}(2)$ baselines. The framework resolves the local-consistency gap by giving it a concrete convex geometry and a minimal differentiable projection, establishing a clean polyhedral baseline. Extending beyond $\mathrm{SA}(2)$ naturally leads to spectrahedral geometries, where curvature encodes global coherence and genuine quantum structure becomes necessary.

Fock State-enhanced Expressivity of Quantum Machine Learning Models

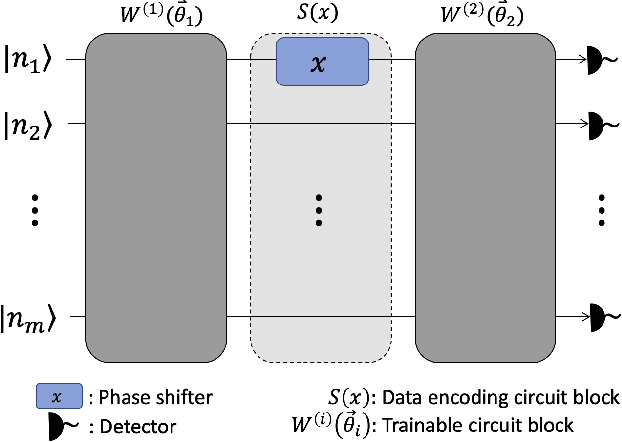
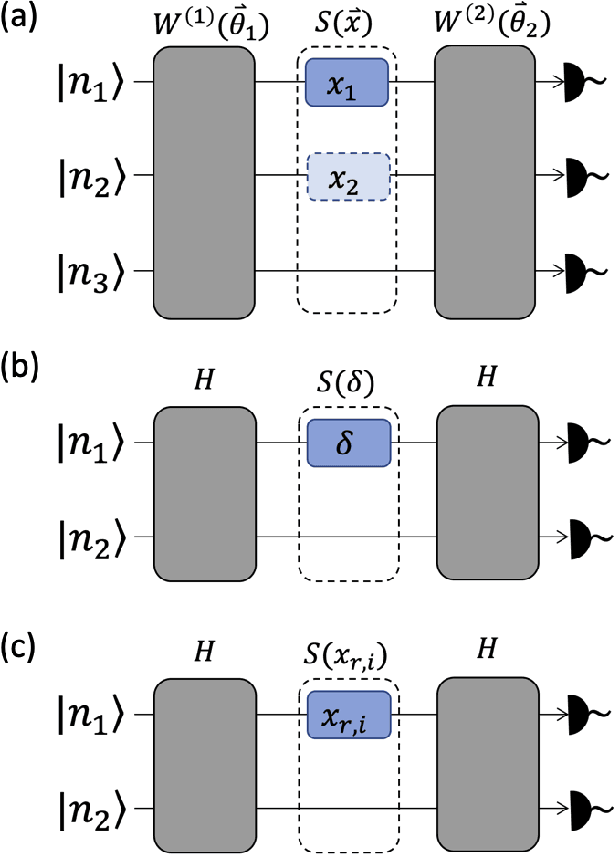
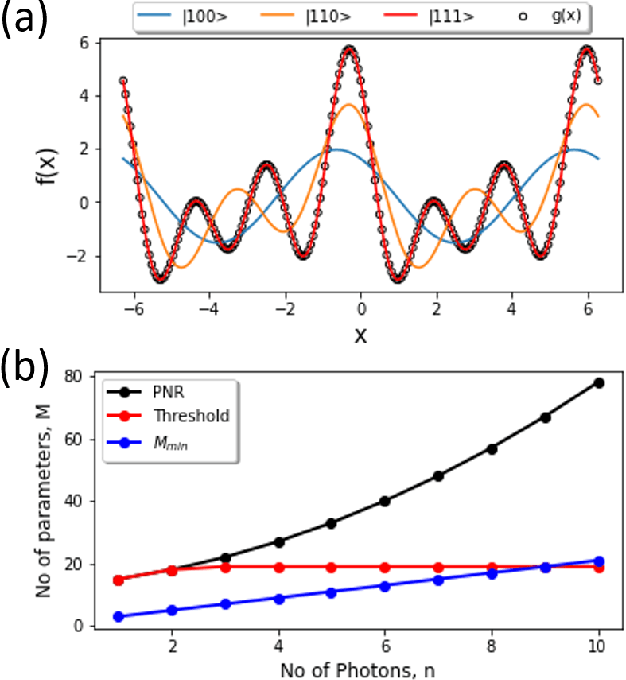
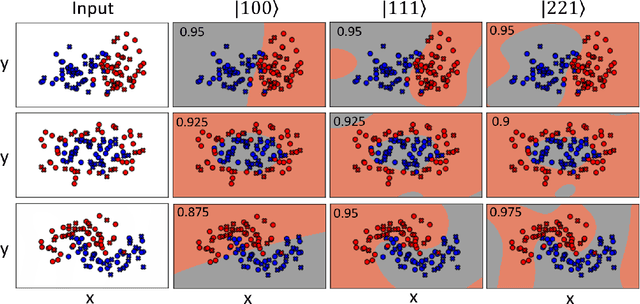
The data-embedding process is one of the bottlenecks of quantum machine learning, potentially negating any quantum speedups. In light of this, more effective data-encoding strategies are necessary. We propose a photonic-based bosonic data-encoding scheme that embeds classical data points using fewer encoding layers and circumventing the need for nonlinear optical components by mapping the data points into the high-dimensional Fock space. The expressive power of the circuit can be controlled via the number of input photons. Our work shed some light on the unique advantages offers by quantum photonics on the expressive power of quantum machine learning models. By leveraging the photon-number dependent expressive power, we propose three different noisy intermediate-scale quantum-compatible binary classification methods with different scaling of required resources suitable for different supervised classification tasks.