Shapley Revisited: Tractable Responsibility Measures for Query Answers

The Shapley value, originating from cooperative game theory, has been employed to define responsibility measures that quantify the contributions of database facts to obtaining a given query answer. For non-numeric queries, this is done by considering a cooperative game whose players are the facts and whose wealth function assigns 1 or 0 to each subset of the database, depending on whether the query answer holds in the given subset. While conceptually simple, this approach suffers from a notable drawback: the problem of computing such Shapley values is #P-hard in data complexity, even for simple conjunctive queries. This motivates us to revisit the question of what constitutes a reasonable responsibility measure and to introduce a new family of responsibility measures -- weighted sums of minimal supports (WSMS) -- which satisfy intuitive properties. Interestingly, while the definition of WSMSs is simple and bears no obvious resemblance to the Shapley value formula, we prove that every WSMS measure can be equivalently seen as the Shapley value of a suitably defined cooperative game. Moreover, WSMS measures enjoy tractable data complexity for a large class of queries, including all unions of conjunctive queries. We further explore the combined complexity of WSMS computation and establish (in)tractability results for various subclasses of conjunctive queries.

Shapley Value Computation in Ontology-Mediated Query Answering

The Shapley value, originally introduced in cooperative game theory for wealth distribution, has found use in KR and databases for the purpose of assigning scores to formulas and database tuples based upon their contribution to obtaining a query result or inconsistency. In the present paper, we explore the use of Shapley values in ontology-mediated query answering (OMQA) and present a detailed complexity analysis of Shapley value computation (SVC) in the OMQA setting. In particular, we establish a PF/#P-hard dichotomy for SVC for ontology-mediated queries (T,q) composed of an ontology T formulated in the description logic ELHI_\bot and a connected constant-free homomorphism-closed query q. We further show that the #P-hardness side of the dichotomy can be strengthened to cover possibly disconnected queries with constants. Our results exploit recently discovered connections between SVC and probabilistic query evaluation and allow us to generalize existing results on probabilistic OMQA.

PDL on Steroids: on Expressive Extensions of PDL with Intersection and Converse

We introduce CPDL+, a family of expressive logics rooted in Propositional Dynamic Logic (PDL). In terms of expressive power, CPDL+ strictly contains PDL extended with intersection and converse (a.k.a. ICPDL) as well as Conjunctive Queries (CQ), Conjunctive Regular Path Queries (CRPQ), or some known extensions thereof (Regular Queries and CQPDL). We investigate the expressive power, characterization of bisimulation, satisfiability, and model checking for CPDL+. We argue that natural subclasses of CPDL+ can be defined in terms of the tree-width of the underlying graphs of the formulas. We show that the class of CPDL+ formulas of tree-width 2 is equivalent to ICPDL, and that it also coincides with CPDL+ formulas of tree-width 1. However, beyond tree-width 2, incrementing the tree-width strictly increases the expressive power. We characterize the expressive power for every class of fixed tree-width formulas in terms of a bisimulation game with pebbles. Based on this characterization, we show that CPDL+ has a tree-like model property. We prove that the satisfiability problem is decidable in 2ExpTime on fixed tree-width formulas, coinciding with the complexity of ICPDL. We also exhibit classes for which satisfiability is reduced to ExpTime. Finally, we establish that the model checking problem for fixed tree-width formulas is in \ptime, contrary to the full class CPDL+.

Containment of Simple Regular Path Queries

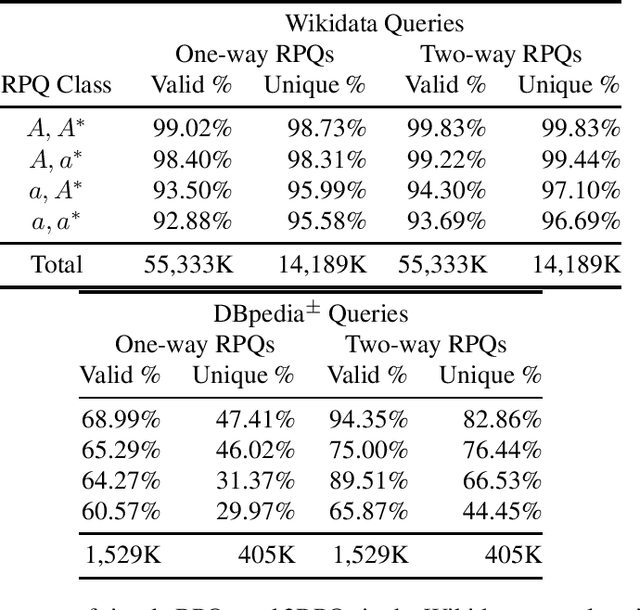
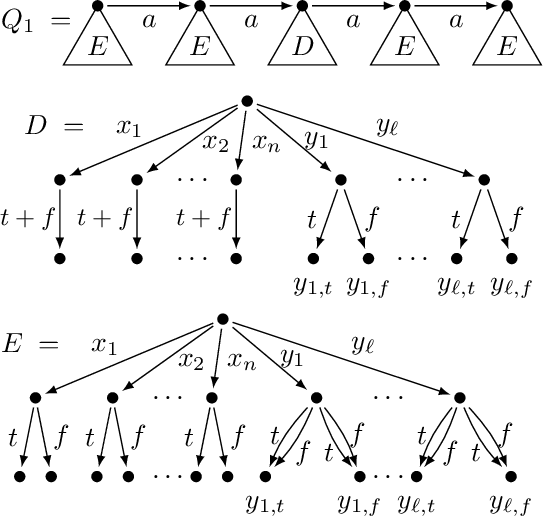
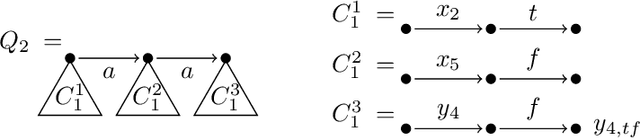
Testing containment of queries is a fundamental reasoning task in knowledge representation. We study here the containment problem for Conjunctive Regular Path Queries (CRPQs), a navigational query language extensively used in ontology and graph database querying. While it is known that containment of CRPQs is expspace-complete in general, we focus here on severely restricted fragments, which are known to be highly relevant in practice according to several recent studies. We obtain a detailed overview of the complexity of the containment problem, depending on the features used in the regular expressions of the queries, with completeness results for np, pitwo, pspace or expspace.