Lipschitz constant estimation for general neural network architectures using control tools

This paper is devoted to the estimation of the Lipschitz constant of neural networks using semidefinite programming. For this purpose, we interpret neural networks as time-varying dynamical systems, where the $k$-th layer corresponds to the dynamics at time $k$. A key novelty with respect to prior work is that we use this interpretation to exploit the series interconnection structure of neural networks with a dynamic programming recursion. Nonlinearities, such as activation functions and nonlinear pooling layers, are handled with integral quadratic constraints. If the neural network contains signal processing layers (convolutional or state space model layers), we realize them as 1-D/2-D/N-D systems and exploit this structure as well. We distinguish ourselves from related work on Lipschitz constant estimation by more extensive structure exploitation (scalability) and a generalization to a large class of common neural network architectures. To show the versatility and computational advantages of our method, we apply it to different neural network architectures trained on MNIST and CIFAR-10.

State space representations of the Roesser type for convolutional layers

From the perspective of control theory, convolutional layers (of neural networks) are 2-D (or N-D) linear time-invariant dynamical systems. The usual representation of convolutional layers by the convolution kernel corresponds to the representation of a dynamical system by its impulse response. However, many analysis tools from control theory, e.g., involving linear matrix inequalities, require a state space representation. For this reason, we explicitly provide a state space representation of the Roesser type for 2-D convolutional layers with $c_\mathrm{in}r_1 + c_\mathrm{out}r_2$ states, where $c_\mathrm{in}$/$c_\mathrm{out}$ is the number of input/output channels of the layer and $r_1$/$r_2$ characterizes the width/length of the convolution kernel. This representation is shown to be minimal for $c_\mathrm{in} = c_\mathrm{out}$. We further construct state space representations for dilated, strided, and N-D convolutions.

Convolutional Neural Networks as 2-D systems

This paper introduces a novel representation of convolutional Neural Networks (CNNs) in terms of 2-D dynamical systems. To this end, the usual description of convolutional layers with convolution kernels, i.e., the impulse responses of linear filters, is realized in state space as a linear time-invariant 2-D system. The overall convolutional Neural Network composed of convolutional layers and nonlinear activation functions is then viewed as a 2-D version of a Lur'e system, i.e., a linear dynamical system interconnected with static nonlinear components. One benefit of this 2-D Lur'e system perspective on CNNs is that we can use robust control theory much more efficiently for Lipschitz constant estimation than previously possible.

Lipschitz constant estimation for 1D convolutional neural networks

In this work, we propose a dissipativity-based method for Lipschitz constant estimation of 1D convolutional neural networks (CNNs). In particular, we analyze the dissipativity properties of convolutional, pooling, and fully connected layers making use of incremental quadratic constraints for nonlinear activation functions and pooling operations. The Lipschitz constant of the concatenation of these mappings is then estimated by solving a semidefinite program which we derive from dissipativity theory. To make our method as efficient as possible, we take the structure of convolutional layers into account realizing these finite impulse response filters as causal dynamical systems in state space and carrying out the dissipativity analysis for the state space realizations. The examples we provide show that our Lipschitz bounds are advantageous in terms of accuracy and scalability.

Neural network training under semidefinite constraints

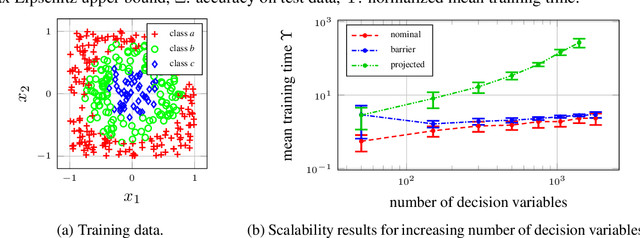
This paper is concerned with the training of neural networks (NNs) under semidefinite constraints. This type of training problems has recently gained popularity since semidefinite constraints can be used to verify interesting properties for NNs that include, e.g., the estimation of an upper bound on the Lipschitz constant, which relates to the robustness of an NN, or the stability of dynamic systems with NN controllers. The utilized semidefinite constraints are based on sector constraints satisfied by the underlying activation functions. Unfortunately, one of the biggest bottlenecks of these new results is the required computational effort for incorporating the semidefinite constraints into the training of NNs which is limiting their scalability to large NNs. We address this challenge by developing interior point methods for NN training that we implement using barrier functions for semidefinite constraints. In order to efficiently compute the gradients of the barrier terms, we exploit the structure of the semidefinite constraints. In experiments, we demonstrate the superior efficiency of our training method over previous approaches, which allows us, e.g., to use semidefinite constraints in the training of Wasserstein generative adversarial networks, where the discriminator must satisfy a Lipschitz condition.

Linear systems with neural network nonlinearities: Improved stability analysis via acausal Zames-Falb multipliers

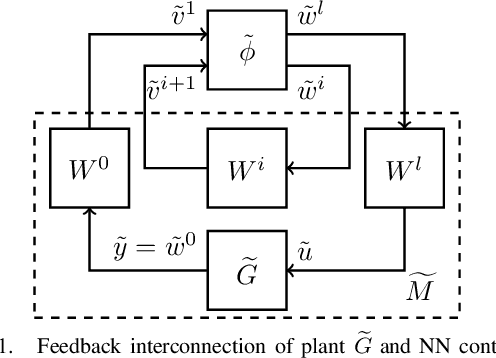
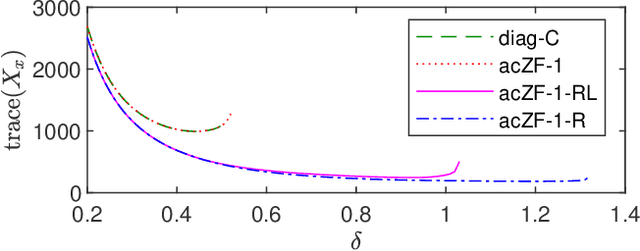
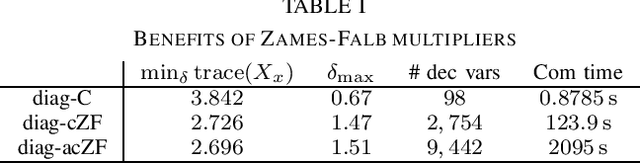
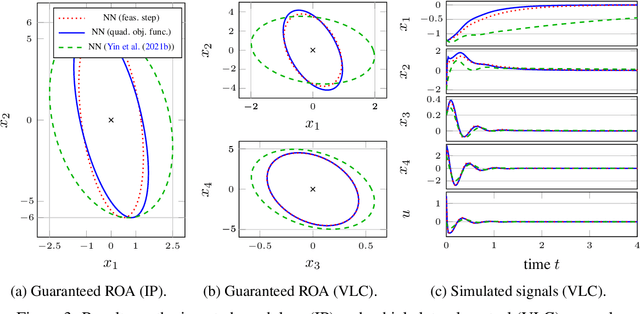
In this paper, we analyze the stability of feedback interconnections of a linear time-invariant system with a neural network nonlinearity in discrete time. Our analysis is based on abstracting neural networks using integral quadratic constraints (IQCs), exploiting the sector-bounded and slope-restricted structure of the underlying activation functions. In contrast to existing approaches, we leverage the full potential of dynamic IQCs to describe the nonlinear activation functions in a less conservative fashion. To be precise, we consider multipliers based on the full-block Yakubovich / circle criterion in combination with acausal Zames-Falb multipliers, leading to linear matrix inequality based stability certificates. Our approach provides a flexible and versatile framework for stability analysis of feedback interconnections with neural network nonlinearities, allowing to trade off computational efficiency and conservatism. Finally, we provide numerical examples that demonstrate the applicability of the proposed framework and the achievable improvements over previous approaches.