Deniz Akdemir
Le Cam Distortion: A Decision-Theoretic Framework for Robust Transfer Learning
Dec 29, 2025Abstract:Distribution shift is the defining challenge of real-world machine learning. The dominant paradigm--Unsupervised Domain Adaptation (UDA)--enforces feature invariance, aligning source and target representations via symmetric divergence minimization [Ganin et al., 2016]. We demonstrate that this approach is fundamentally flawed: when domains are unequally informative (e.g., high-quality vs degraded sensors), strict invariance necessitates information destruction, causing "negative transfer" that can be catastrophic in safety-critical applications [Wang et al., 2019]. We propose a decision-theoretic framework grounded in Le Cam's theory of statistical experiments [Le Cam, 1986], using constructive approximations to replace symmetric invariance with directional simulability. We introduce Le Cam Distortion, quantified by the Deficiency Distance $δ(E_1, E_2)$, as a rigorous upper bound for transfer risk conditional on simulability. Our framework enables transfer without source degradation by learning a kernel that simulates the target from the source. Across five experiments (genomics, vision, reinforcement learning), Le Cam Distortion achieves: (1) near-perfect frequency estimation in HLA genomics (correlation $r=0.999$, matching classical methods), (2) zero source utility loss in CIFAR-10 image classification (81.2% accuracy preserved vs 34.7% drop for CycleGAN), and (3) safe policy transfer in RL control where invariance-based methods suffer catastrophic collapse. Le Cam Distortion provides the first principled framework for risk-controlled transfer learning in domains where negative transfer is unacceptable: medical imaging, autonomous systems, and precision medicine.
TabMixNN: A Unified Deep Learning Framework for Structural Mixed Effects Modeling on Tabular Data
Dec 29, 2025Abstract:We present TabMixNN, a flexible PyTorch-based deep learning framework that synthesizes classical mixed-effects modeling with modern neural network architectures for tabular data analysis. TabMixNN addresses the growing need for methods that can handle hierarchical data structures while supporting diverse outcome types including regression, classification, and multitask learning. The framework implements a modular three-stage architecture: (1) a mixed-effects encoder with variational random effects and flexible covariance structures, (2) backbone architectures including Generalized Structural Equation Models (GSEM) and spatial-temporal manifold networks, and (3) outcome-specific prediction heads supporting multiple outcome families. Key innovations include an R-style formula interface for accessibility, support for directed acyclic graph (DAG) constraints for causal structure learning, Stochastic Partial Differential Equation (SPDE) kernels for spatial modeling, and comprehensive interpretability tools including SHAP values and variance decomposition. We demonstrate the framework's flexibility through applications to longitudinal data analysis, genomic prediction, and spatial-temporal modeling. TabMixNN provides a unified interface for researchers to leverage deep learning while maintaining the interpretability and theoretical grounding of classical mixed-effects models.
Likelihood-Preserving Embeddings for Statistical Inference
Dec 27, 2025Abstract:Modern machine learning embeddings provide powerful compression of high-dimensional data, yet they typically destroy the geometric structure required for classical likelihood-based statistical inference. This paper develops a rigorous theory of likelihood-preserving embeddings: learned representations that can replace raw data in likelihood-based workflows -- hypothesis testing, confidence interval construction, model selection -- without altering inferential conclusions. We introduce the Likelihood-Ratio Distortion metric $Δ_n$, which measures the maximum error in log-likelihood ratios induced by an embedding. Our main theoretical contribution is the Hinge Theorem, which establishes that controlling $Δ_n$ is necessary and sufficient for preserving inference. Specifically, if the distortion satisfies $Δ_n = o_p(1)$, then (i) all likelihood-ratio based tests and Bayes factors are asymptotically preserved, and (ii) surrogate maximum likelihood estimators are asymptotically equivalent to full-data MLEs. We prove an impossibility result showing that universal likelihood preservation requires essentially invertible embeddings, motivating the need for model-class-specific guarantees. We then provide a constructive framework using neural networks as approximate sufficient statistics, deriving explicit bounds connecting training loss to inferential guarantees. Experiments on Gaussian and Cauchy distributions validate the sharp phase transition predicted by exponential family theory, and applications to distributed clinical inference demonstrate practical utility.
Selection of training populations (and other subset selection problems) with an accelerated genetic algorithm (STPGA: An R-package for selection of training populations with a genetic algorithm)
Feb 26, 2017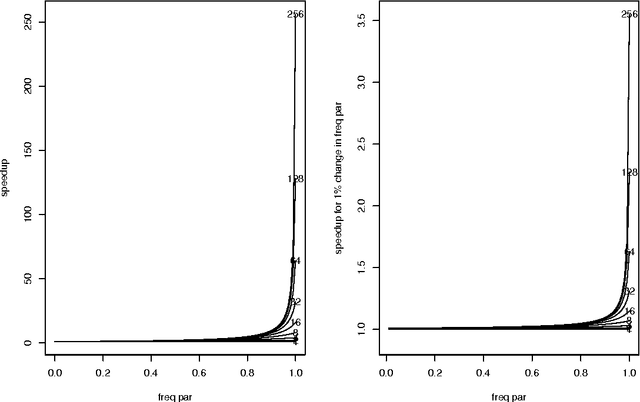
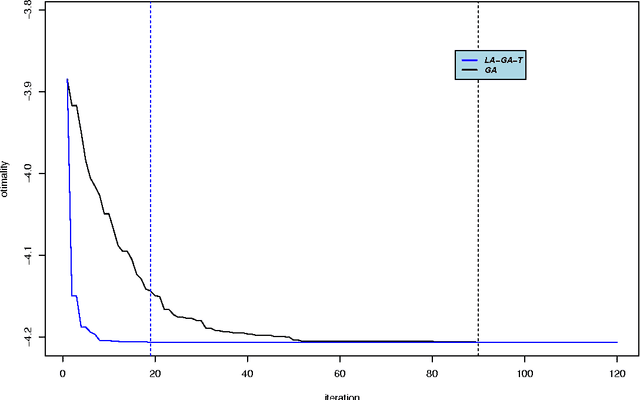
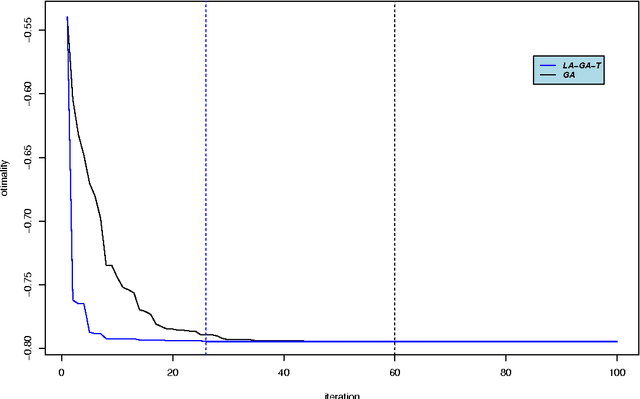
Abstract:Optimal subset selection is an important task that has numerous algorithms designed for it and has many application areas. STPGA contains a special genetic algorithm supplemented with a tabu memory property (that keeps track of previously tried solutions and their fitness for a number of iterations), and with a regression of the fitness of the solutions on their coding that is used to form the ideal estimated solution (look ahead property) to search for solutions of generic optimal subset selection problems. I have initially developed the programs for the specific problem of selecting training populations for genomic prediction or association problems, therefore I give discussion of the theory behind optimal design of experiments to explain the default optimization criteria in STPGA, and illustrate the use of the programs in this endeavor. Nevertheless, I have picked a few other areas of application: supervised and unsupervised variable selection based on kernel alignment, supervised variable selection with design criteria, influential observation identification for regression, solving mixed integer quadratic optimization problems, balancing gains and inbreeding in a breeding population. Some of these illustrations pertain new statistical approaches.
Locally Epistatic Models for Genome-wide Prediction and Association by Importance Sampling
Mar 29, 2016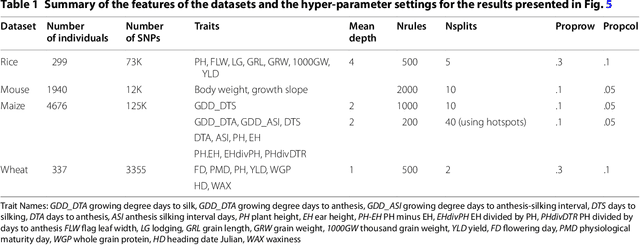
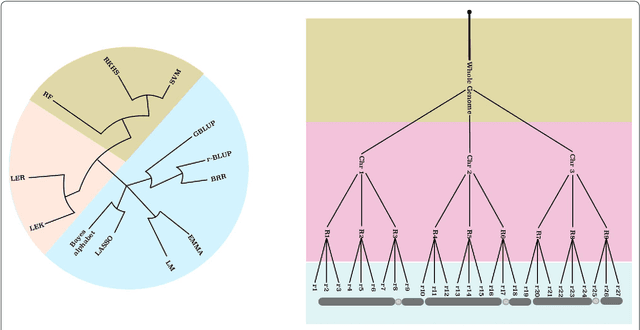

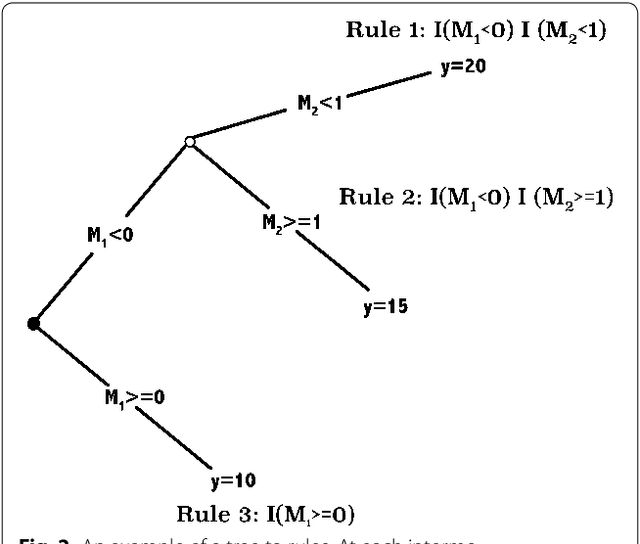
Abstract:In statistical genetics an important task involves building predictive models for the genotype-phenotype relationships and thus attribute a proportion of the total phenotypic variance to the variation in genotypes. Numerous models have been proposed to incorporate additive genetic effects into models for prediction or association. However, there is a scarcity of models that can adequately account for gene by gene or other forms of genetical interactions. In addition, there is an increased interest in using marker annotations in genome-wide prediction and association. In this paper, we discuss an hybrid modeling methodology which combines the parametric mixed modeling approach and the non-parametric rule ensembles. This approach gives us a flexible class of models that can be used to capture additive, locally epistatic genetic effects, gene x background interactions and allows us to incorporate one or more annotations into the genomic selection or association models. We use benchmark data sets covering a range of organisms and traits in addition to simulated data sets to illustrate the strengths of this approach. The improvement of model accuracies and association results suggest that a part of the "missing heritability" in complex traits can be captured by modeling local epistasis.
Likelihood Estimation with Incomplete Array Variate Observations
Jan 05, 2015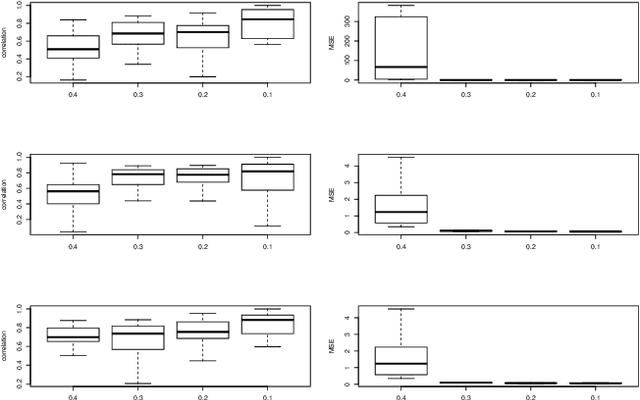
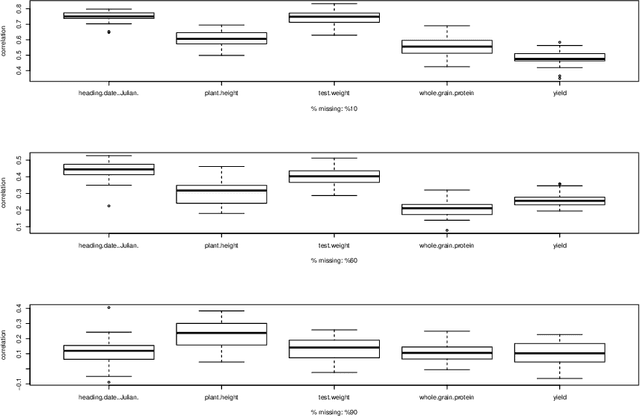
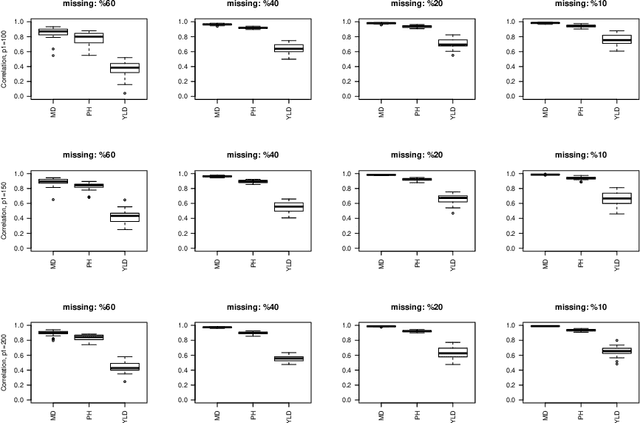
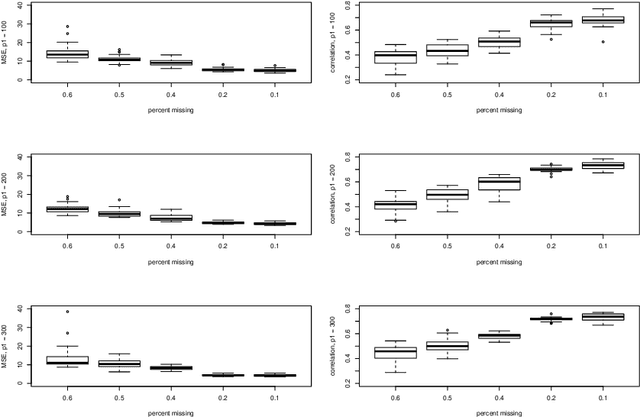
Abstract:Missing data is an important challenge when dealing with high dimensional data arranged in the form of an array. In this paper, we propose methods for estimation of the parameters of array variate normal probability model from partially observed multiway data. The methods developed here are useful for missing data imputation, estimation of mean and covariance parameters for multiway data. A multiway semi-parametric mixed effects model that allows separation of multiway covariance effects is also defined and an efficient algorithm for estimation is recommended. We provide simulation results along with real life data from genetics to demonstrate these methods.
Genomic Prediction of Quantitative Traits using Sparse and Locally Epistatic Models
Feb 10, 2014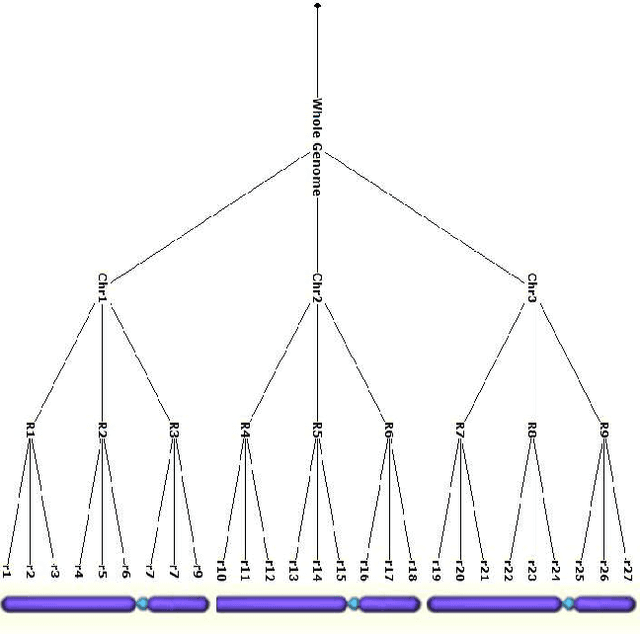
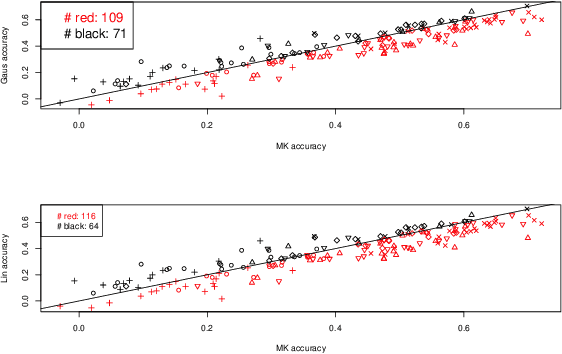
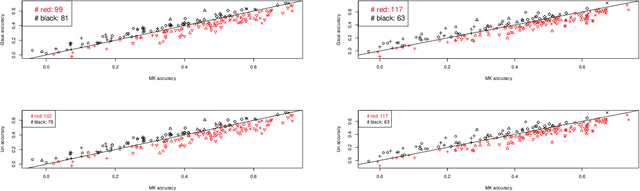
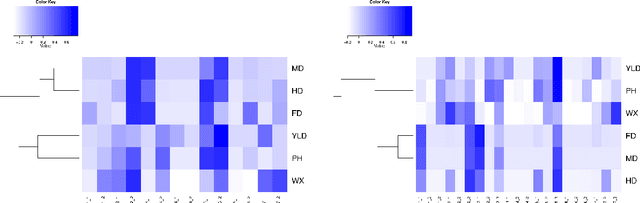
Abstract:In plant and animal breeding studies a distinction is made between the genetic value (additive + epistatic genetic effects) and the breeding value (additive genetic effects) of an individual since it is expected that some of the epistatic genetic effects will be lost due to recombination. In this paper, we argue that the breeder can take advantage of some of the epistatic marker effects in regions of low recombination. The models introduced here aim to estimate local epistatic line heritability by using the genetic map information and combine the local additive and epistatic effects. To this end, we have used semi-parametric mixed models with multiple local genomic relationship matrices with hierarchical designs and lasso post-processing for sparsity in the final model. Our models produce good predictive performance along with good explanatory information.
Locally epistatic genomic relationship matrices for genomic association, prediction and selection
Aug 14, 2013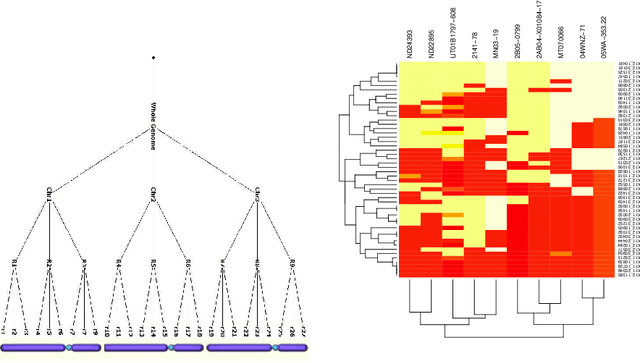

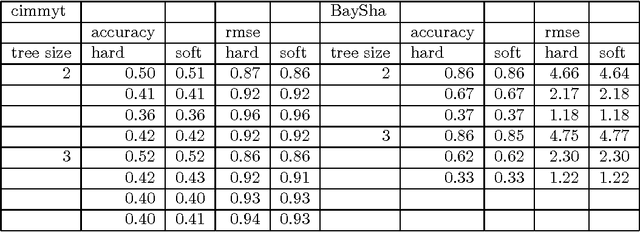
Abstract:As the amount and complexity of genetic information increases it is necessary that we explore some efficient ways of handling these data. This study takes the "divide and conquer" approach for analyzing high dimensional genomic data. Our aims include reducing the dimensionality of the problem that has to be dealt one at a time, improving the performance and interpretability of the models. We propose using the inherent structures in the genome; to divide the bigger problem into manageable parts. In plant and animal breeding studies a distinction is made between the commercial value (additive + epistatic genetic effects) and the breeding value (additive genetic effects) of an individual since it is expected that some of the epistatic genetic effects will be lost due to recombination. In this paper, we argue that the breeder can take advantage of some of the epistatic marker effects in regions of low recombination. The models introduced here aim to estimate local epistatic line heritability by using the genetic map information and combine the local additive and epistatic effects. To this end, we have used semi-parametric mixed models with multiple local genomic relationship matrices with hierarchical testing designs and lasso post-processing for sparsity in the final model and speed. Our models produce good predictive performance along with genetic association information.
Soft Rule Ensembles for Statistical Learning
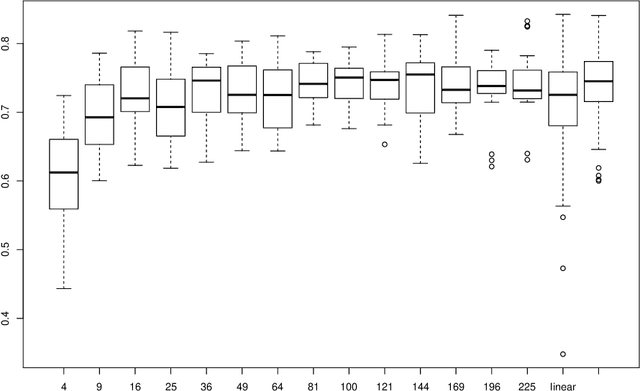
Feb 22, 2013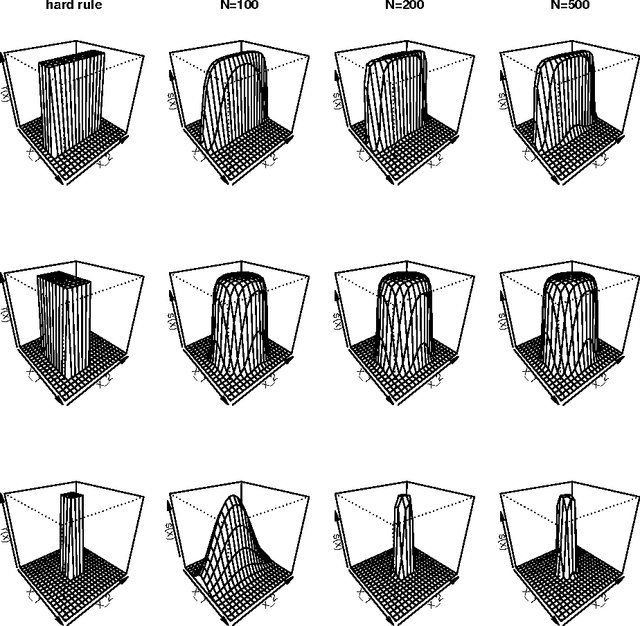
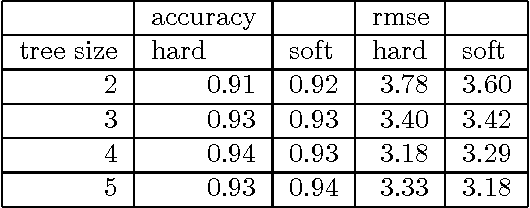
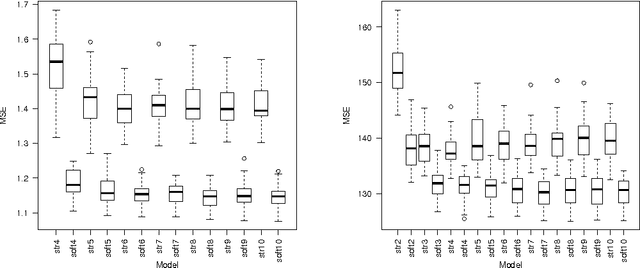
Abstract:In this article supervised learning problems are solved using soft rule ensembles. We first review the importance sampling learning ensembles (ISLE) approach that is useful for generating hard rules. The soft rules are then obtained with logistic regression from the corresponding hard rules. In order to deal with the perfect separation problem related to the logistic regression, Firth's bias corrected likelihood is used. Various examples and simulation results show that soft rule ensembles can improve predictive performance over hard rule ensembles.
Ensemble Clustering with Logic Rules
Nov 15, 2012Abstract:In this article, the logic rule ensembles approach to supervised learning is applied to the unsupervised or semi-supervised clustering. Logic rules which were obtained by combining simple conjunctive rules are used to partition the input space and an ensemble of these rules is used to define a similarity matrix. Similarity partitioning is used to partition the data in an hierarchical manner. We have used internal and external measures of cluster validity to evaluate the quality of clusterings or to identify the number of clusters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge