Information Theoretic Perspective on Representation Learning

An information-theoretic framework is introduced to analyze last-layer embedding, focusing on learned representations for regression tasks. We define representation-rate and derive limits on the reliability with which input-output information can be represented as is inherently determined by the input-source entropy. We further define representation capacity in a perturbed setting, and representation rate-distortion for a compressed output. We derive the achievable capacity, the achievable representation-rate, and their converse. Finally, we combine the results in a unified setting.

On Inverse Problems, Parameter Estimation, and Domain Generalization

Signal restoration and inverse problems are key elements in most real-world data science applications. In the past decades, with the emergence of machine learning methods, inversion of measurements has become a popular step in almost all physical applications, which is normally executed prior to downstream tasks that often involve parameter estimation. In this work, we analyze the general problem of parameter estimation in an inverse problem setting. First, we address the domain-shift problem by re-formulating it in direct relation with the discrete parameter estimation analysis. We analyze a significant vulnerability in current attempts to enforce domain generalization, which we dubbed the Double Meaning Theorem. Our theoretical findings are experimentally illustrated for domain shift examples in image deblurring and speckle suppression in medical imaging. We then proceed to a theoretical analysis of parameter estimation given observed measurements before and after data processing involving an inversion of the observations. We compare this setting for invertible and non-invertible (degradation) processes. We distinguish between continuous and discrete parameter estimation, corresponding with regression and classification problems, respectively. Our theoretical findings align with the well-known information-theoretic data processing inequality, and to a certain degree question the common misconception that data-processing for inversion, based on modern generative models that may often produce outstanding perceptual quality, will necessarily improve the following parameter estimation objective. It is our hope that this paper will provide practitioners with deeper insights that may be leveraged in the future for the development of more efficient and informed strategic system planning, critical in safety-sensitive applications.

One-Shot Image Restoration

Image restoration, or inverse problems in image processing, has long been an extensively studied topic. In recent years supervised learning approaches have become a popular strategy attempting to tackle this task. Unfortunately, most supervised learning-based methods are highly demanding in terms of computational resources and training data (sample complexity). In addition, trained models are sensitive to domain changes, such as varying acquisition systems, signal sampling rates, resolution and contrast. In this work, we try to answer a fundamental question: Can supervised learning models generalize well solely by learning from one image or even part of an image? If so, then what is the minimal amount of patches required to achieve acceptable generalization? To this end, we focus on an efficient patch-based learning framework that requires a single image input-output pair for training. Experimental results demonstrate the applicability, robustness and computational efficiency of the proposed approach for supervised image deblurring and super-resolution. Our results showcase significant improvement of learning models' sample efficiency, generalization and time complexity, that can hopefully be leveraged for future real-time applications, and applied to other signals and modalities.

Back to Basics: Fast Denoising Iterative Algorithm

We introduce Back to Basics (BTB), a fast iterative algorithm for noise reduction. Our method is computationally efficient, does not require training or ground truth data, and can be applied in the presence of independent noise, as well as correlated (coherent) noise, where the noise level is unknown. We examine three study cases: natural image denoising in the presence of additive white Gaussian noise, Poisson-distributed image denoising, and speckle suppression in optical coherence tomography (OCT). Experimental results demonstrate that the proposed approach can effectively improve image quality, in challenging noise settings. Theoretical guarantees are provided for convergence stability.

Domain-Aware Few-Shot Learning for Optical Coherence Tomography Noise Reduction

Speckle noise has long been an extensively studied problem in medical imaging. In recent years, there have been significant advances in leveraging deep learning methods for noise reduction. Nevertheless, adaptation of supervised learning models to unseen domains remains a challenging problem. Specifically, deep neural networks (DNNs) trained for computational imaging tasks are vulnerable to changes in the acquisition system's physical parameters, such as: sampling space, resolution, and contrast. Even within the same acquisition system, performance degrades across datasets of different biological tissues. In this work, we propose a few-shot supervised learning framework for optical coherence tomography (OCT) noise reduction, that offers a dramatic increase in training speed and requires only a single image, or part of an image, and a corresponding speckle suppressed ground truth, for training. Furthermore, we formulate the domain shift problem for OCT diverse imaging systems, and prove that the output resolution of a despeckling trained model is determined by the source domain resolution. We also provide possible remedies. We propose different practical implementations of our approach, verify and compare their applicability, robustness, and computational efficiency. Our results demonstrate significant potential for generally improving sample complexity, generalization, and time efficiency, for coherent and non-coherent noise reduction via supervised learning models, that can also be leveraged for other real-time computer vision applications.

Less is More: Rethinking Few-Shot Learning and Recurrent Neural Nets

The statistical supervised learning framework assumes an input-output set with a joint probability distribution that is reliably represented by the training dataset. The learner is then required to output a prediction rule learned from the training dataset's input-output pairs. In this work, we provide meaningful insights into the asymptotic equipartition property (AEP) \citep{Shannon:1948} in the context of machine learning, and illuminate some of its potential ramifications for few-shot learning. We provide theoretical guarantees for reliable learning under the information-theoretic AEP, and for the generalization error with respect to the sample size. We then focus on a highly efficient recurrent neural net (RNN) framework and propose a reduced-entropy algorithm for few-shot learning. We also propose a mathematical intuition for the RNN as an approximation of a sparse coding solver. We verify the applicability, robustness, and computational efficiency of the proposed approach with image deblurring and optical coherence tomography (OCT) speckle suppression. Our experimental results demonstrate significant potential for improving learning models' sample efficiency, generalization, and time complexity, that can therefore be leveraged for practical real-time applications.

Convolutional Sparse Coding Fast Approximation with Application to Seismic Reflectivity Estimation

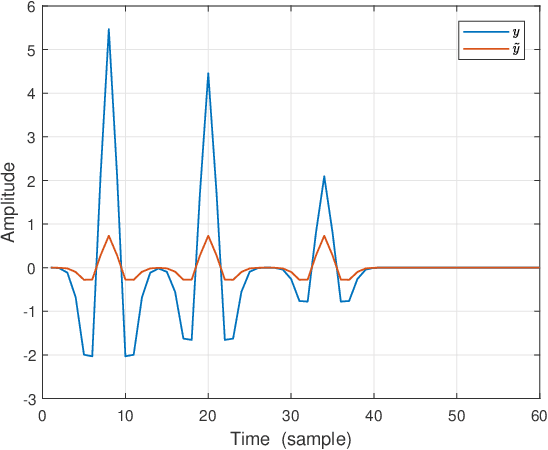
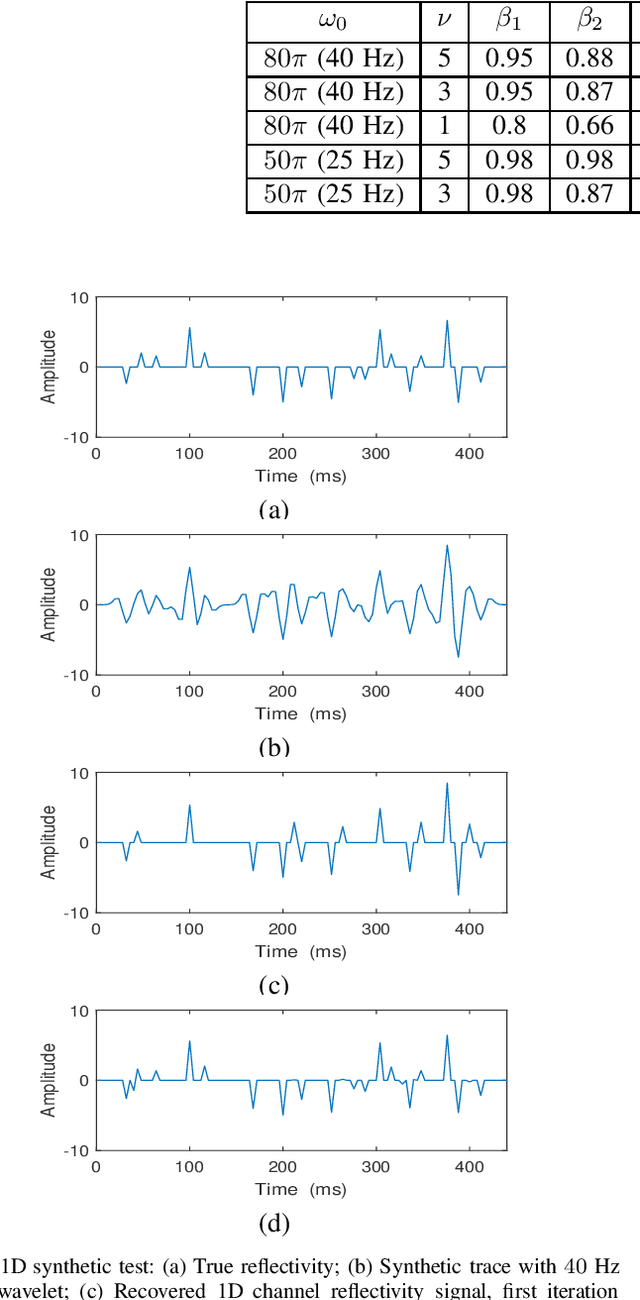
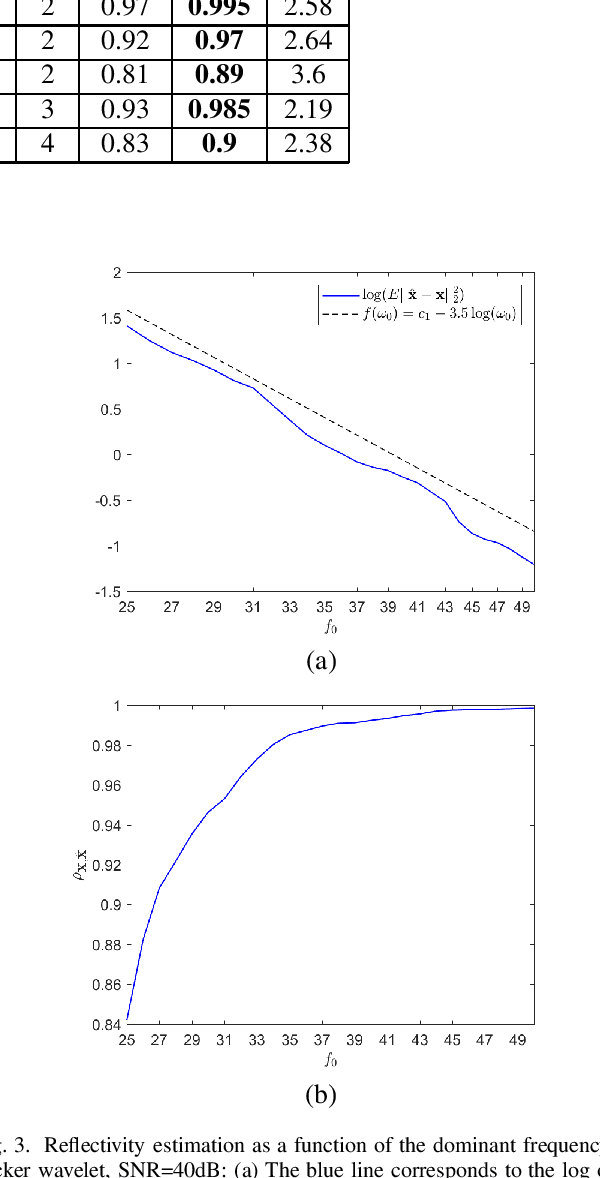
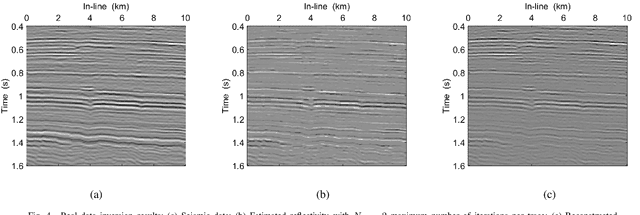
In sparse coding, we attempt to extract features of input vectors, assuming that the data is inherently structured as a sparse superposition of basic building blocks. Similarly, neural networks perform a given task by learning features of the training data set. Recently both data-driven and model-driven feature extracting methods have become extremely popular and have achieved remarkable results. Nevertheless, practical implementations are often too slow to be employed in real-life scenarios, especially for real-time applications. We propose a speed-up upgraded version of the classic iterative thresholding algorithm, that produces a good approximation of the convolutional sparse code within 2-5 iterations. The speed advantage is gained mostly from the observation that most solvers are slowed down by inefficient global thresholding. The main idea is to normalize each data point by the local receptive field energy, before applying a threshold. This way, the natural inclination towards strong feature expressions is suppressed, so that one can rely on a global threshold that can be easily approximated, or learned during training. The proposed algorithm can be employed with a known predetermined dictionary, or with a trained dictionary. The trained version is implemented as a neural net designed as the unfolding of the proposed solver. The performance of the proposed solution is demonstrated via the seismic inversion problem in both synthetic and real data scenarios. We also provide theoretical guarantees for a stable support recovery. Namely, we prove that under certain conditions the true support is perfectly recovered within the first iteration.

Blind Deconvolution via Maximum Kurtosis Adaptive Filtering

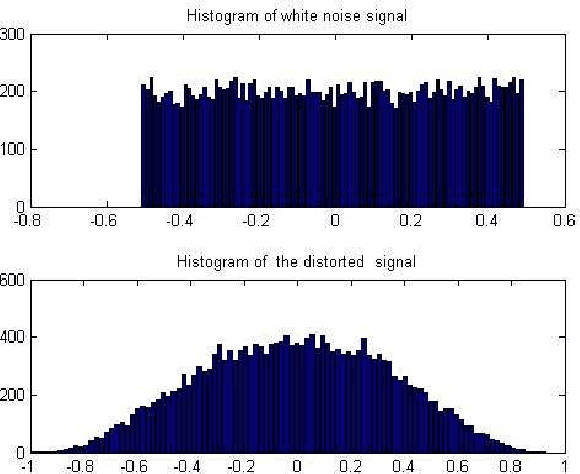
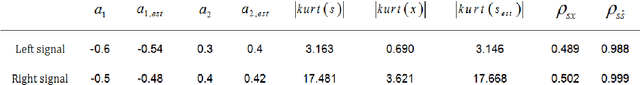
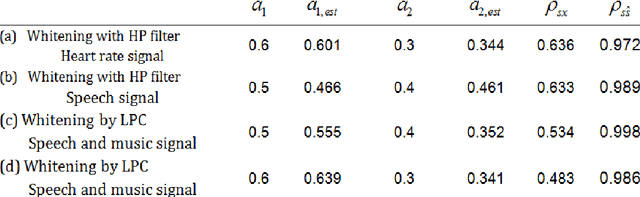
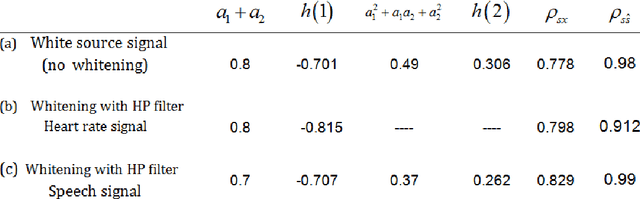
In this paper, we present an algorithm for identifying a parametrically described destructive unknown system based on a non-gaussianity measure. It is known that under certain conditions the output of a linear system is more gaussian than the input. Hence, an inverse filter is searched, such that its output is minimally gaussian. We use the kurtosis as a measure of the non-gaussianity of the signal. A maximum of the kurtosis as a function of the deconvolving filter coefficients is searched. The search is done iteratively using the gradient ascent algorithm, and the coefficients at the maximum point correspond to the inverse filter coefficients. This filter may be applied to the distorted signal to obtain the original undistorted signal. While a similar approach has been used before, it was always directed at a particular kind of a signal, commonly of impulsive characteristics. In this paper a successful attempt has been made to apply the algorithm to a wider range of signals, such as to process distorted audio signals and destructed images. This innovative implementation required the revelation of a way to preprocess the distorted signal at hand. The experimental results show very good performance in terms of recovering audio signals and blurred images, both for an FIR and IIR distorting filters.