Communication Efficient Decentralization for Smoothed Online Convex Optimization

We study the multi-agent Smoothed Online Convex Optimization (SOCO) problem, where $N$ agents interact through a communication graph. In each round, each agent $i$ receives a strongly convex hitting cost function $f^i_t$ in an online fashion and selects an action $x^i_t \in \mathbb{R}^d$. The objective is to minimize the global cumulative cost, which includes the sum of individual hitting costs $f^i_t(x^i_t)$, a temporal "switching cost" for changing decisions, and a spatial "dissimilarity cost" that penalizes deviations in decisions among neighboring agents. We propose the first decentralized algorithm for multi-agent SOCO and prove its asymptotic optimality. Our approach allows each agent to operate using only local information from its immediate neighbors in the graph. For finite-time performance, we establish that the optimality gap in competitive ratio decreases with the time horizon $T$ and can be conveniently tuned based on the per-round computation available to each agent. Moreover, our results hold even when the communication graph changes arbitrarily and adaptively over time. Finally, we establish that the computational complexity per round depends only logarithmically on the number of agents and almost linearly on their degree within the graph, ensuring scalability for large-system implementations.

Best of Both Worlds: Stochastic and Adversarial Convex Function Chasing

Convex function chasing (CFC) is an online optimization problem in which during each round $t$, a player plays an action $x_t$ in response to a hitting cost $f_t(x_t)$ and an additional cost of $c(x_t,x_{t-1})$ for switching actions. We study the CFC problem in stochastic and adversarial environments, giving algorithms that achieve performance guarantees simultaneously in both settings. Specifically, we consider the squared $\ell_2$-norm switching costs and a broad class of quadratic hitting costs for which the sequence of minimizers either forms a martingale or is chosen adversarially. This is the first work that studies the CFC problem using a stochastic framework. We provide a characterization of the optimal stochastic online algorithm and, drawing a comparison between the stochastic and adversarial scenarios, we demonstrate that the adversarial-optimal algorithm exhibits suboptimal performance in the stochastic context. Motivated by this, we provide a best-of-both-worlds algorithm that obtains robust adversarial performance while simultaneously achieving near-optimal stochastic performance.

Online Optimization with Untrusted Predictions

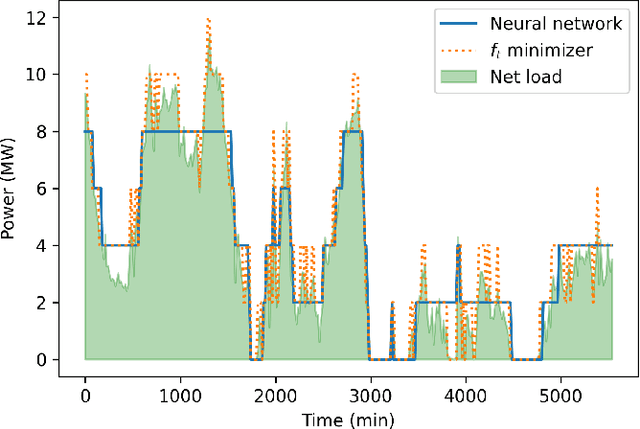
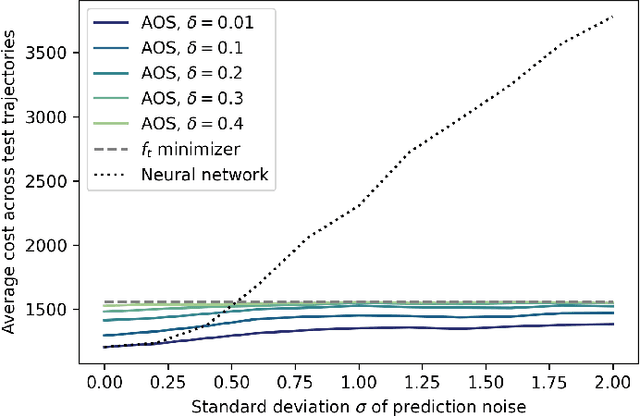
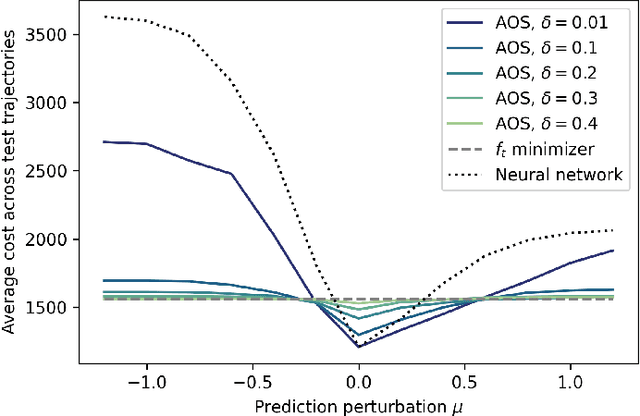
We examine the problem of online optimization, where a decision maker must sequentially choose points in a general metric space to minimize the sum of per-round, non-convex hitting costs and the costs of switching decisions between rounds. The decision maker has access to a black-box oracle, such as a machine learning model, that provides untrusted and potentially inaccurate predictions of the optimal decision in each round. The goal of the decision maker is to exploit the predictions if they are accurate, while guaranteeing performance that is not much worse than the hindsight optimal sequence of decisions, even when predictions are inaccurate. We impose the standard assumption that hitting costs are globally $\alpha$-polyhedral. We propose a novel algorithm, Adaptive Online Switching (AOS), and prove that, for any desired $\delta > 0$, it is $(1+2\delta)$-competitive if predictions are perfect, while also maintaining a uniformly bounded competitive ratio of $2^{\tilde{\mathcal{O}}(1/(\alpha \delta))}$ even when predictions are adversarial. Further, we prove that this trade-off is necessary and nearly optimal in the sense that any deterministic algorithm which is $(1+\delta)$-competitive if predictions are perfect must be at least $2^{\tilde{\Omega}(1/(\alpha \delta))}$-competitive when predictions are inaccurate.

A New Approach to Capacity Scaling Augmented With Unreliable Machine Learning Predictions

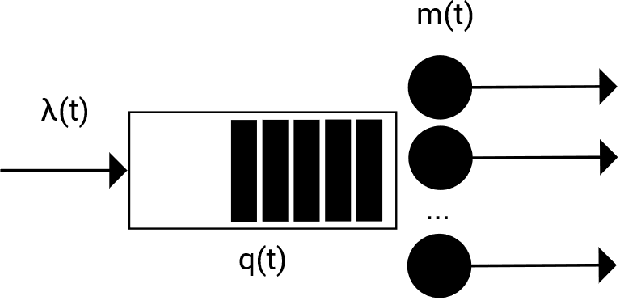
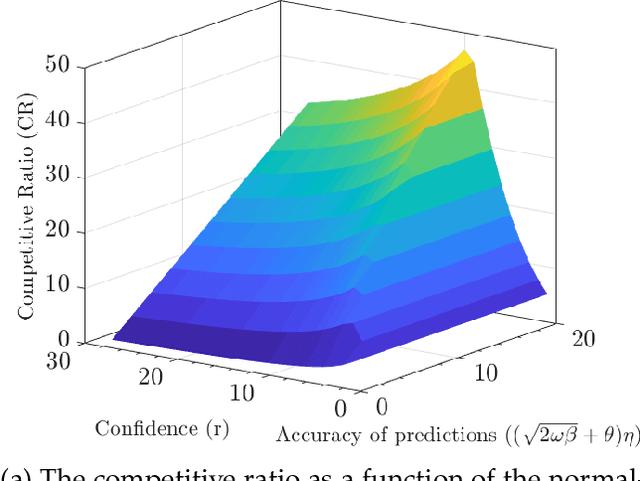
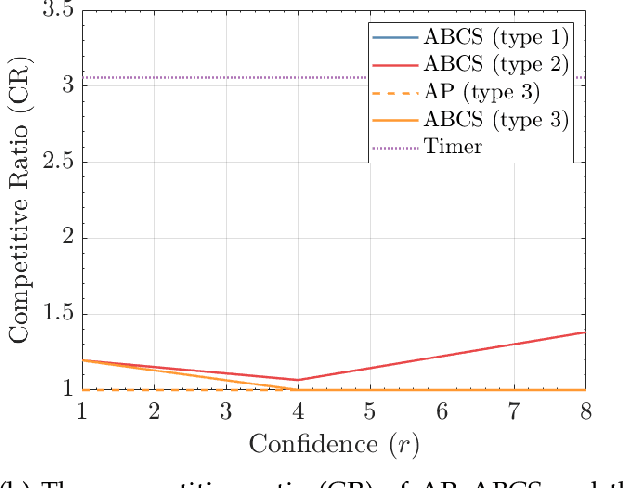
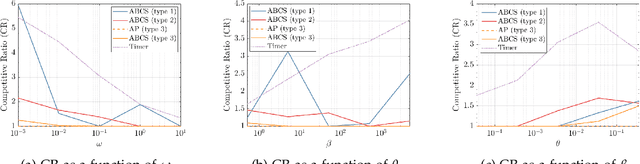
Modern data centers suffer from immense power consumption. The erratic behavior of internet traffic forces data centers to maintain excess capacity in the form of idle servers in case the workload suddenly increases. As an idle server still consumes a significant fraction of the peak energy, data center operators have heavily invested in capacity scaling solutions. In simple terms, these aim to deactivate servers if the demand is low and to activate them again when the workload increases. To do so, an algorithm needs to strike a delicate balance between power consumption, flow-time, and switching costs. Over the last decade, the research community has developed competitive online algorithms with worst-case guarantees. In the presence of historic data patterns, prescription from Machine Learning (ML) predictions typically outperform such competitive algorithms. This, however, comes at the cost of sacrificing the robustness of performance, since unpredictable surges in the workload are not uncommon. The current work builds on the emerging paradigm of augmenting unreliable ML predictions with online algorithms to develop novel robust algorithms that enjoy the benefits of both worlds. We analyze a continuous-time model for capacity scaling, where the goal is to minimize the weighted sum of flow-time, switching cost, and power consumption in an online fashion. We propose a novel algorithm, called Adaptive Balanced Capacity Scaling (ABCS), that has access to black-box ML predictions, but is completely oblivious to the accuracy of these predictions. In particular, if the predictions turn out to be accurate in hindsight, we prove that ABCS is $(1+\varepsilon)$-competitive. Moreover, even when the predictions are inaccurate, ABCS guarantees a bounded competitive ratio. The performance of the ABCS algorithm on a real-world dataset positively support the theoretical results.