Causal Characterization of Measurement and Mechanistic Anomalies

Root cause analysis of anomalies aims to identify those features that cause the deviation from the normal process. Existing methods ignore, however, that anomalies can arise through two fundamentally different processes: measurement errors, where data was generated normally but one or more values were recorded incorrectly, and mechanism shifts, where the causal process generating the data changed. While measurement errors can often be safely corrected, mechanistic anomalies require careful consideration. We define a causal model that explicitly captures both types by treating outliers as latent interventions on latent ("true") and observed ("measured") variables. We show that they are identifiable, and propose a maximum likelihood estimation approach to put this to practice. Experiments show that our method matches state-of-the-art performance in root cause localization, while it additionally enables accurate classification of anomaly types, and remains robust even when the causal DAG is unknown.

We Are Not Your Real Parents: Telling Causal from Confounded using MDL

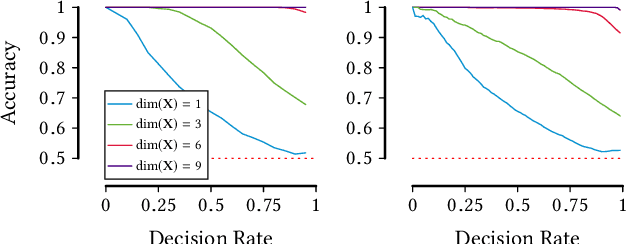
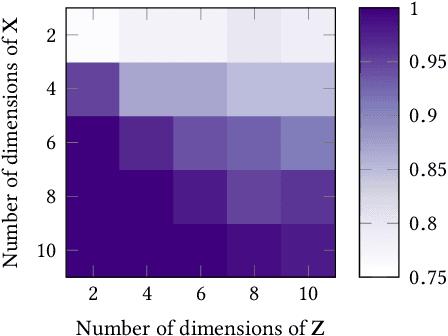
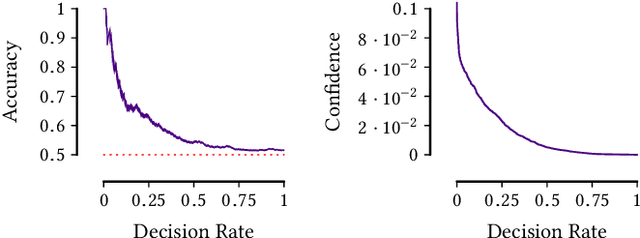
Given data over variables $(X_1,...,X_m, Y)$ we consider the problem of finding out whether $X$ jointly causes $Y$ or whether they are all confounded by an unobserved latent variable $Z$. To do so, we take an information-theoretic approach based on Kolmogorov complexity. In a nutshell, we follow the postulate that first encoding the true cause, and then the effects given that cause, results in a shorter description than any other encoding of the observed variables. The ideal score is not computable, and hence we have to approximate it. We propose to do so using the Minimum Description Length (MDL) principle. We compare the MDL scores under the models where $X$ causes $Y$ and where there exists a latent variables $Z$ confounding both $X$ and $Y$ and show our scores are consistent. To find potential confounders we propose using latent factor modeling, in particular, probabilistic PCA (PPCA). Empirical evaluation on both synthetic and real-world data shows that our method, CoCa, performs very well -- even when the true generating process of the data is far from the assumptions made by the models we use. Moreover, it is robust as its accuracy goes hand in hand with its confidence.