David Castanon
Learning Bregman Divergences
Jun 06, 2019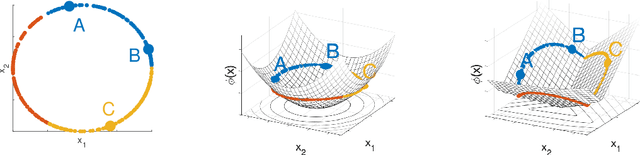
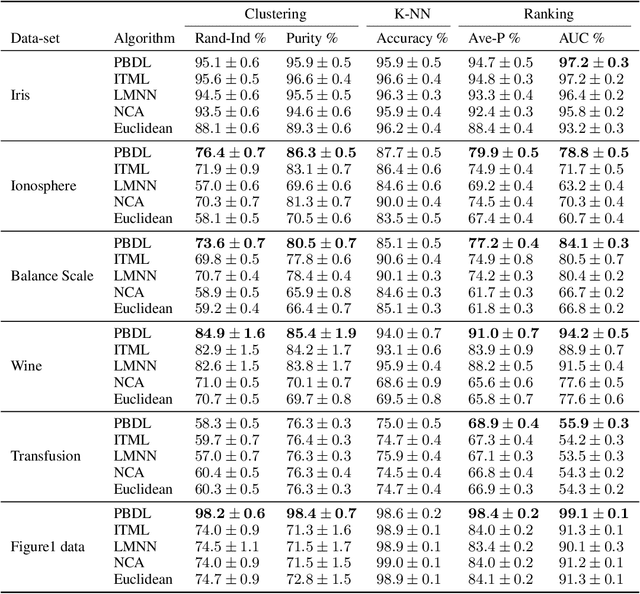
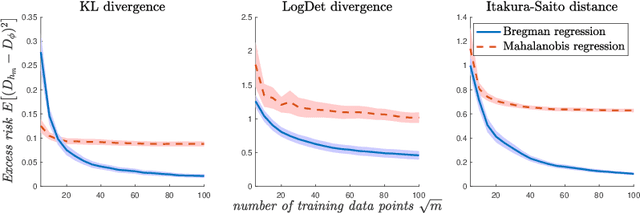
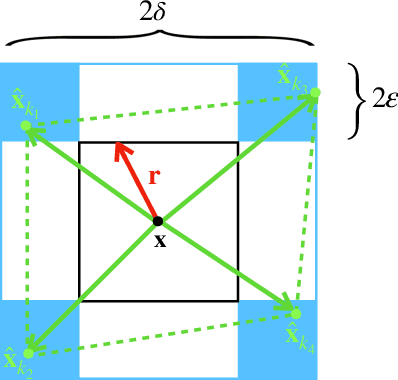
Abstract:Metric learning is the problem of learning a task-specific distance function given supervision. Classical linear methods for this problem (known as Mahalanobis metric learning approaches) are well-studied both theoretically and empirically, but are limited to Euclidean distances after learned linear transformations of the input space. In this paper, we consider learning a Bregman divergence, a rich and important class of divergences that includes Mahalanobis metrics as a special case but also includes the KL-divergence and others. We develop a formulation and algorithm for learning arbitrary Bregman divergences based on approximating their underlying convex generating function via a piecewise linear function. We show several theoretical results of our resulting model, including a PAC guarantee that the learned Bregman divergence approximates an arbitrary Bregman divergence with error O_p (m^(-1/(d+2))), where m is the number of training points and d is the dimension of the data. We provide empirical results on using the learned divergences for classification, semi-supervised clustering, and ranking problems.
Multi-Stage Classifier Design
Jan 29, 2013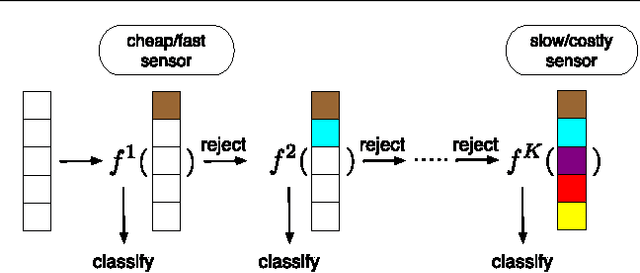

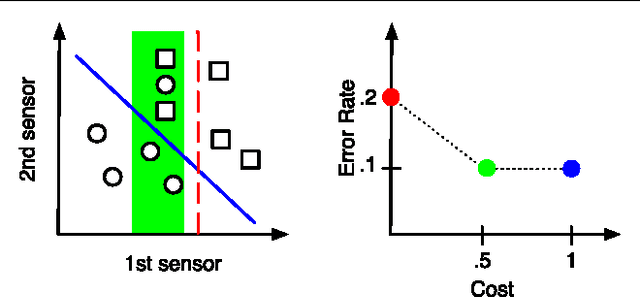
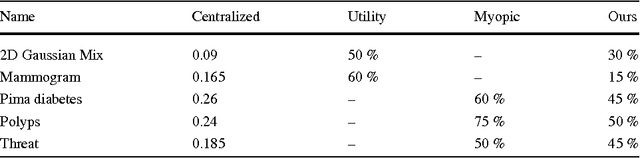
Abstract:In many classification systems, sensing modalities have different acquisition costs. It is often {\it unnecessary} to use every modality to classify a majority of examples. We study a multi-stage system in a prediction time cost reduction setting, where the full data is available for training, but for a test example, measurements in a new modality can be acquired at each stage for an additional cost. We seek decision rules to reduce the average measurement acquisition cost. We formulate an empirical risk minimization problem (ERM) for a multi-stage reject classifier, wherein the stage $k$ classifier either classifies a sample using only the measurements acquired so far or rejects it to the next stage where more attributes can be acquired for a cost. To solve the ERM problem, we show that the optimal reject classifier at each stage is a combination of two binary classifiers, one biased towards positive examples and the other biased towards negative examples. We use this parameterization to construct stage-by-stage global surrogate risk, develop an iterative algorithm in the boosting framework and present convergence and generalization results. We test our work on synthetic, medical and explosives detection datasets. Our results demonstrate that substantial cost reduction without a significant sacrifice in accuracy is achievable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge