Posterior Contraction Rates for Graph-Based Semi-Supervised Classification

This paper studies Bayesian nonparametric estimation of a binary regression function in a semi-supervised setting. We assume that the features are supported on a hidden manifold, and use unlabeled data to construct a sequence of graph-based priors over the regression function restricted to the given features. We establish contraction rates for the corresponding graph-based posteriors, interpolated to be supported over regression functions on the underlying manifold. Minimax optimal contraction rates are achieved under certain conditions. Our results provide novel understanding on why and how unlabeled data are helpful in Bayesian semi-supervised classification.

Local Regularization of Noisy Point Clouds: Improved Global Geometric Estimates and Data Analysis

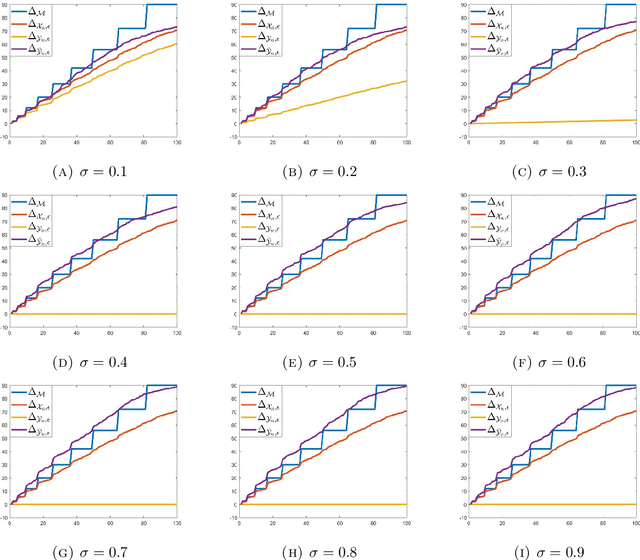
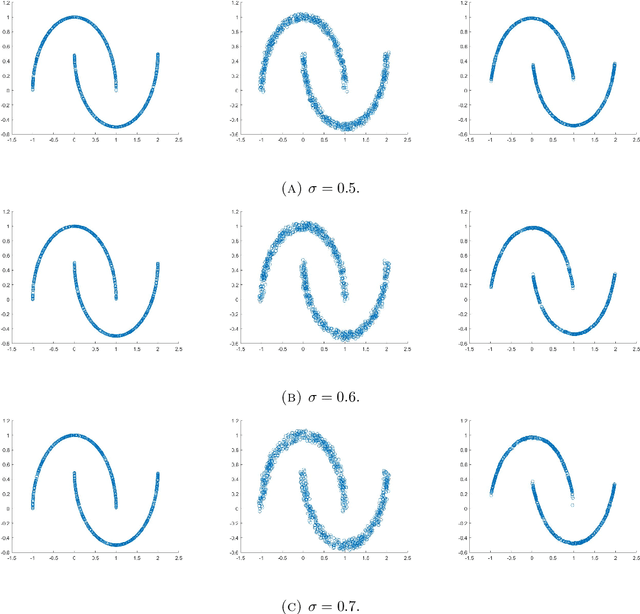
Several data analysis techniques employ similarity relationships between data points to uncover the intrinsic dimension and geometric structure of the underlying data-generating mechanism. In this paper we work under the model assumption that the data is made of random perturbations of feature vectors lying on a low-dimensional manifold. We study two questions: how to define the similarity relationship over noisy data points, and what is the resulting impact of the choice of similarity in the extraction of global geometric information from the underlying manifold. We provide concrete mathematical evidence that using a local regularization of the noisy data to define the similarity improves the approximation of the hidden Euclidean distance between unperturbed points. Furthermore, graph-based objects constructed with the locally regularized similarity function satisfy better error bounds in their recovery of global geometric ones. Our theory is supported by numerical experiments that demonstrate that the gain in geometric understanding facilitated by local regularization translates into a gain in classification accuracy in simulated and real data.

Variational Characterizations of Local Entropy and Heat Regularization in Deep Learning

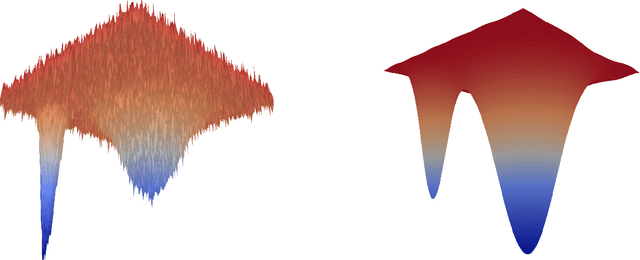
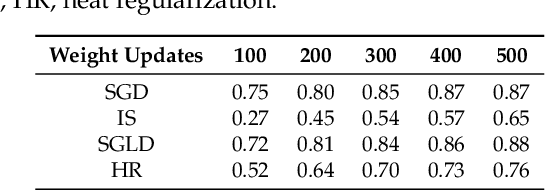
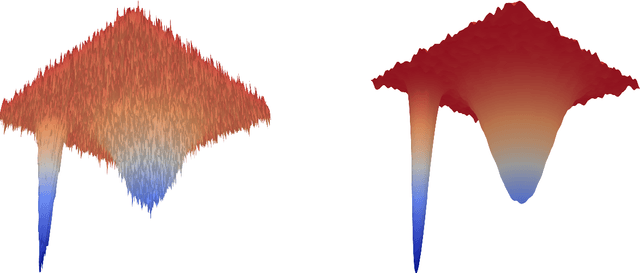
The aim of this paper is to provide new theoretical and computational understanding on two loss regularizations employed in deep learning, known as local entropy and heat regularization. For both regularized losses we introduce variational characterizations that naturally suggest a two-step scheme for their optimization, based on the iterative shift of a probability density and the calculation of a best Gaussian approximation in Kullback-Leibler divergence. Under this unified light, the optimization schemes for local entropy and heat regularized loss differ only over which argument of the Kullback-Leibler divergence is used to find the best Gaussian approximation. Local entropy corresponds to minimizing over the second argument, and the solution is given by moment matching. This allows to replace traditional back-propagation calculation of gradients by sampling algorithms, opening an avenue for gradient-free, parallelizable training of neural networks.

On the Consistency of Graph-based Bayesian Learning and the Scalability of Sampling Algorithms

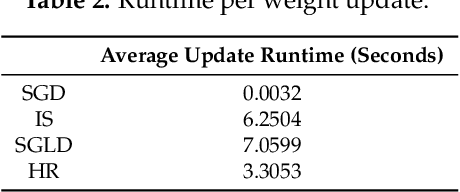
A popular approach to semi-supervised learning proceeds by endowing the input data with a graph structure in order to extract geometric information and incorporate it into a Bayesian framework. We introduce new theory that gives appropriate scalings of graph parameters that provably lead to a well-defined limiting posterior as the size of the unlabeled data set grows. Furthermore, we show that these consistency results have profound algorithmic implications. When consistency holds, carefully designed graph-based Markov chain Monte Carlo algorithms are proved to have a uniform spectral gap, independent of the number of unlabeled inputs. Several numerical experiments corroborate both the statistical consistency and the algorithmic scalability established by the theory.

Continuum Limit of Posteriors in Graph Bayesian Inverse Problems

We consider the problem of recovering a function input of a differential equation formulated on an unknown domain $M$. We assume to have access to a discrete domain $M_n=\{x_1, \dots, x_n\} \subset M$, and to noisy measurements of the output solution at $p\le n$ of those points. We introduce a graph-based Bayesian inverse problem, and show that the graph-posterior measures over functions in $M_n$ converge, in the large $n$ limit, to a posterior over functions in $M$ that solves a Bayesian inverse problem with known domain. The proofs rely on the variational formulation of the Bayesian update, and on a new topology for the study of convergence of measures over functions on point clouds to a measure over functions on the continuum. Our framework, techniques, and results may serve to lay the foundations of robust uncertainty quantification of graph-based tasks in machine learning. The ideas are presented in the concrete setting of recovering the initial condition of the heat equation on an unknown manifold.