Conserved active information

We introduce conserved active information $I^\oplus$, a symmetric extension of active information that quantifies net information gain/loss across the entire search space, respecting No-Free-Lunch conservation. Through Bernoulli and uniform-baseline examples, we show $I^\oplus$ reveals regimes hidden from KL divergence, such as when strong knowledge reduces global disorder. Such regimes are proven formally under uniform baseline, distinguishing disorder (increasing mild knowledge from order-imposing strong knowledge. We further illustrate these regimes with examples from Markov chains and cosmological fine-tuning. This resolves a longstanding critique of active information while enabling applications in search, optimization, and beyond.

Forecast Ergodicity: Prediction Modeling Using Algorithmic Information Theory

The capabilities of machine intelligence are bounded by the potential of data from the past to forecast the future. Deep learning tools are used to find structures in the available data to make predictions about the future. Such structures have to be present in the available data in the first place and they have to be applicable in the future. Forecast ergodicity is a measure of the ability to forecast future events from data in the past. We model this bound by the algorithmic complexity of the available data.

Mode hunting through active information

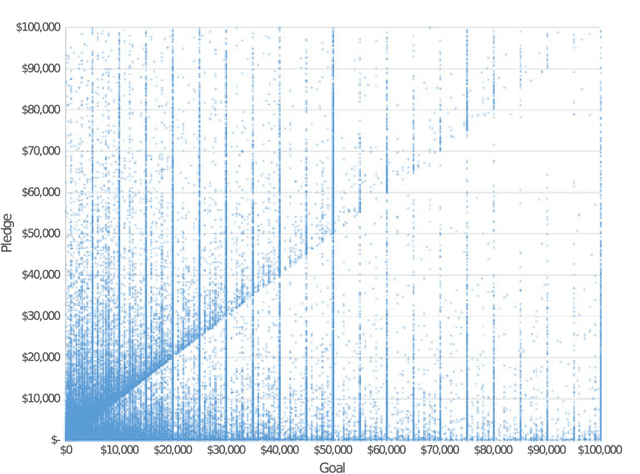
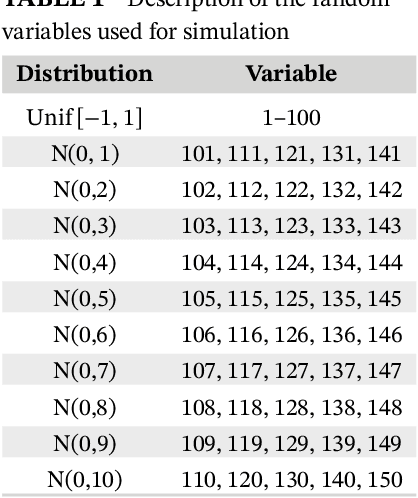
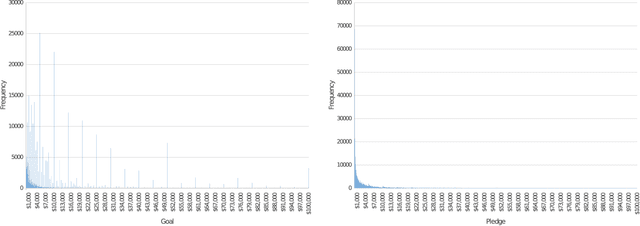
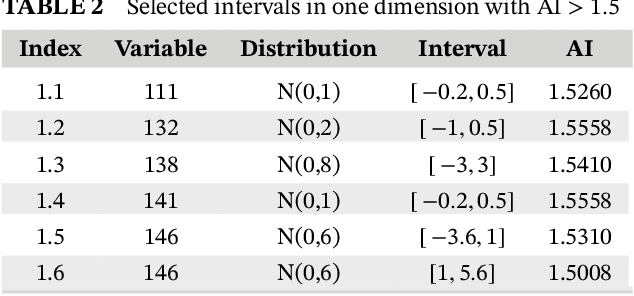
We propose a new method to find modes based on active information. We develop an algorithm that, when applied to the whole space, will say whether there are any modes present \textit{and} where they are; this algorithm will reduce the dimensionality without resorting to Principal Components; and more importantly, population-wise, will not detect modes when they are not present.