Transfer Learning Across Fixed-Income Product Classes

We propose a framework for transfer learning of discount curves across different fixed-income product classes. Motivated by challenges in estimating discount curves from sparse or noisy data, we extend kernel ridge regression (KR) to a vector-valued setting, formulating a convex optimization problem in a vector-valued reproducing kernel Hilbert space (RKHS). Each component of the solution corresponds to the discount curve implied by a specific product class. We introduce an additional regularization term motivated by economic principles, promoting smoothness of spread curves between product classes, and show that it leads to a valid separable kernel structure. A main theoretical contribution is a decomposition of the vector-valued RKHS norm induced by separable kernels. We further provide a Gaussian process interpretation of vector-valued KR, enabling quantification of estimation uncertainty. Illustrative examples demonstrate that transfer learning significantly improves extrapolation performance and tightens confidence intervals compared to single-curve estimation.

Kernel Density Machines

We introduce kernel density machines (KDM), a novel density ratio estimator in a reproducing kernel Hilbert space setting. KDM applies to general probability measures on countably generated measurable spaces without restrictive assumptions on continuity, or the existence of a Lebesgue density. For computational efficiency, we incorporate a low-rank approximation with precisely controlled error that grants scalability to large-sample settings. We provide rigorous theoretical guarantees, including asymptotic consistency, a functional central limit theorem, and finite-sample error bounds, establishing a strong foundation for practical use. Empirical results based on simulated and real data demonstrate the efficacy and precision of KDM.

Joint Estimation of Conditional Mean and Covariance for Unbalanced Panels

We propose a novel nonparametric kernel-based estimator of cross-sectional conditional mean and covariance matrices for large unbalanced panels. We show its consistency and provide finite-sample guarantees. In an empirical application, we estimate conditional mean and covariance matrices for a large unbalanced panel of monthly stock excess returns given macroeconomic and firm-specific covariates from 1962 to 2021.The estimator performs well with respect to statistical measures. It is informative for empirical asset pricing, generating conditional mean-variance efficient portfolios with substantial out-of-sample Sharpe ratios far beyond equal-weighted benchmarks.

Adaptive joint distribution learning

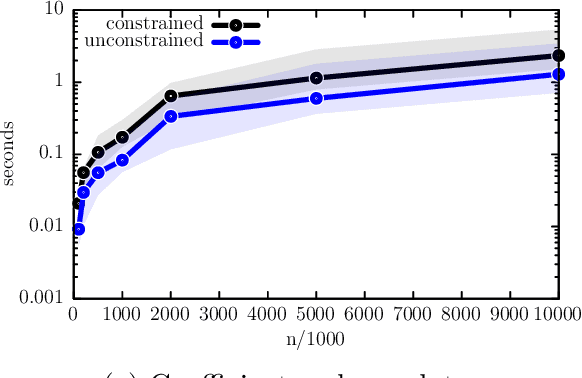
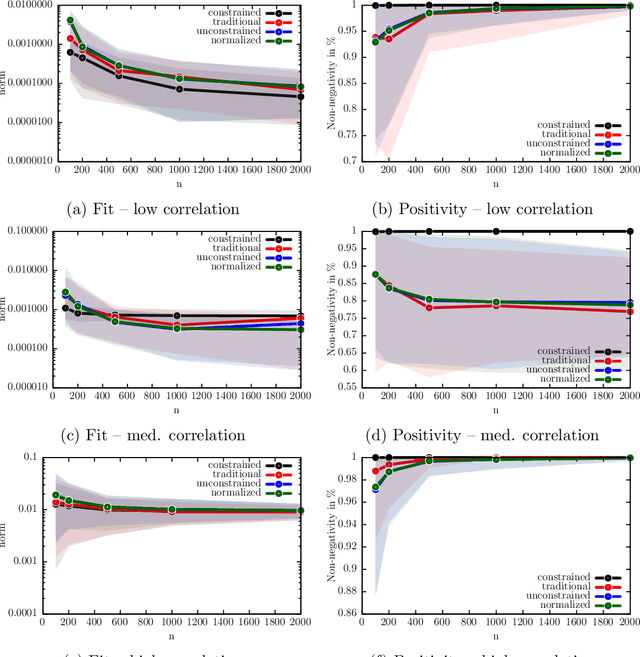
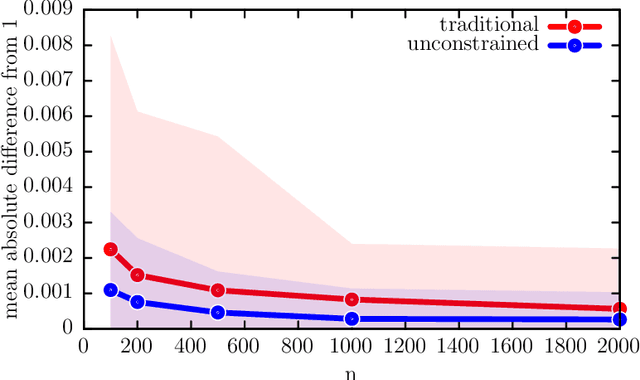
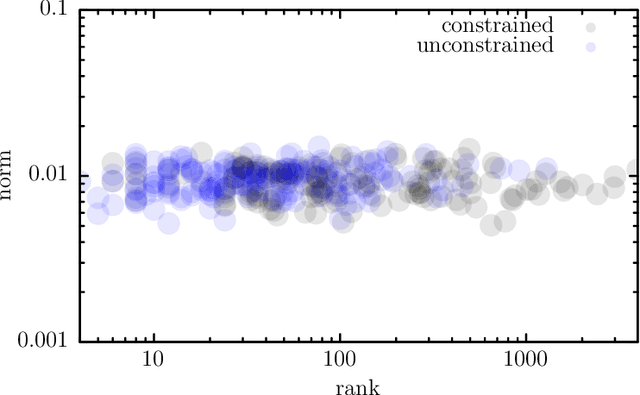
We develop a new framework for embedding (joint) probability distributions in tensor product reproducing kernel Hilbert spaces (RKHS). This framework accommodates a low-dimensional, positive, and normalized model of a Radon-Nikodym derivative, estimated from sample sizes of up to several million data points, alleviating the inherent limitations of RKHS modeling. Well-defined normalized and positive conditional distributions are natural by-products to our approach. The embedding is fast to compute and naturally accommodates learning problems ranging from prediction to classification. The theoretical findings are supplemented by favorable numerical results.