Clustering of Nonnegative Data and an Application to Matrix Completion

In this paper, we propose a simple algorithm to cluster nonnegative data lying in disjoint subspaces. We analyze its performance in relation to a certain measure of correlation between said subspaces. We use our clustering algorithm to develop a matrix completion algorithm which can outperform standard matrix completion algorithms on data matrices satisfying certain natural conditions.

Lower Memory Oblivious (Tensor) Subspace Embeddings with Fewer Random Bits: Modewise Methods for Least Squares

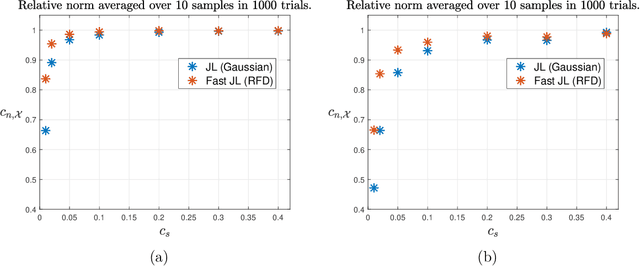
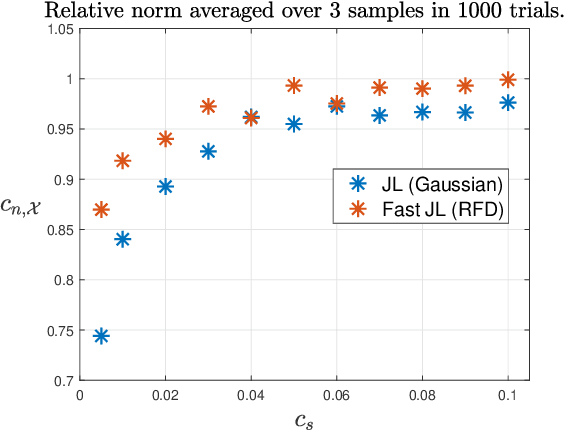
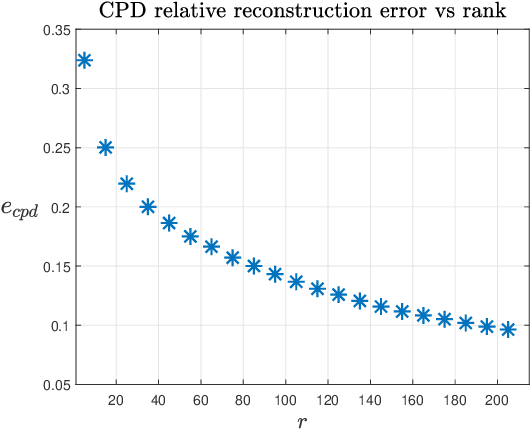
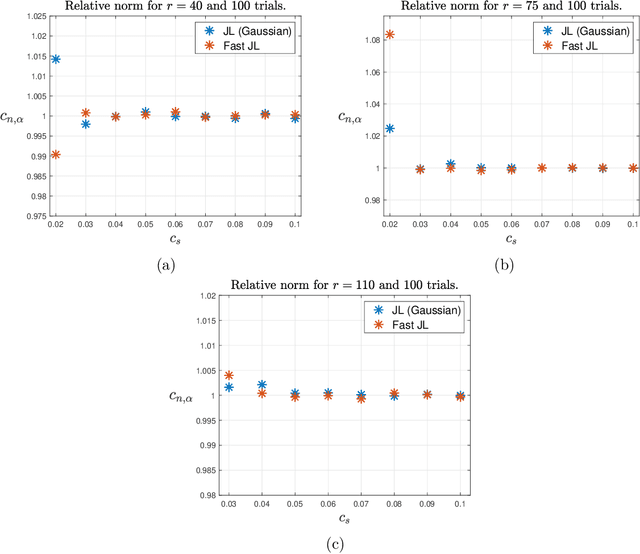
In this paper new general modewise Johnson-Lindenstrauss (JL) subspace embeddings are proposed that are both considerably faster to generate and easier to store than traditional JL embeddings when working with extremely large vectors and/or tensors. Corresponding embedding results are then proven for two different types of low-dimensional (tensor) subspaces. The first of these new subspace embedding results produces improved space complexity bounds for embeddings of rank-$r$ tensors whose CP decompositions are contained in the span of a fixed (but unknown) set of $r$ rank-one basis tensors. In the traditional vector setting this first result yields new and very general near-optimal oblivious subspace embedding constructions that require fewer random bits to generate than standard JL embeddings when embedding subspaces of $\mathbb{C}^N$ spanned by basis vectors with special Kronecker structure. The second result proven herein provides new fast JL embeddings of arbitrary $r$-dimensional subspaces $\mathcal{S} \subset \mathbb{C}^N$ which also require fewer random bits (and so are easier to store - i.e., require less space) than standard fast JL embedding methods in order to achieve small $\epsilon$-distortions. These new oblivious subspace embedding results work by $(i)$ effectively folding any given vector in $\mathcal{S}$ into a (not necessarily low-rank) tensor, and then $(ii)$ embedding the resulting tensor into $\mathbb{C}^m$ for $m \leq C r \log^c(N) / \epsilon^2$. Applications related to compression and fast compressed least squares solution methods are also considered, including those used for fitting low-rank CP decompositions, and the proposed JL embedding results are shown to work well numerically in both settings.

Spectral Clustering: An empirical study of Approximation Algorithms and its Application to the Attrition Problem

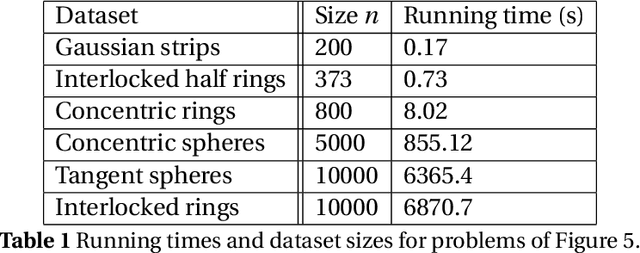
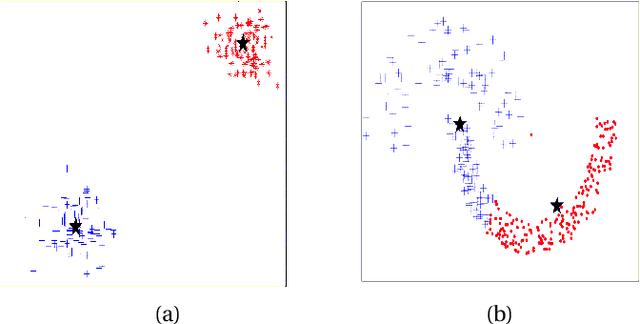
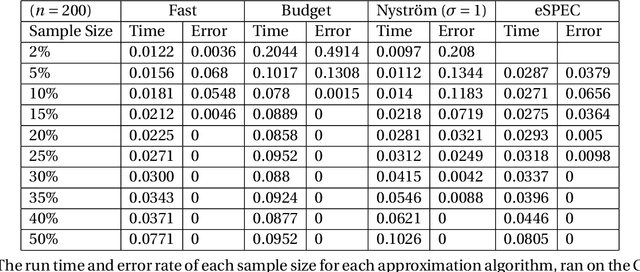
Clustering is the problem of separating a set of objects into groups (called clusters) so that objects within the same cluster are more similar to each other than to those in different clusters. Spectral clustering is a now well-known method for clustering which utilizes the spectrum of the data similarity matrix to perform this separation. Since the method relies on solving an eigenvector problem, it is computationally expensive for large datasets. To overcome this constraint, approximation methods have been developed which aim to reduce running time while maintaining accurate classification. In this article, we summarize and experimentally evaluate several approximation methods for spectral clustering. From an applications standpoint, we employ spectral clustering to solve the so-called attrition problem, where one aims to identify from a set of employees those who are likely to voluntarily leave the company from those who are not. Our study sheds light on the empirical performance of existing approximate spectral clustering methods and shows the applicability of these methods in an important business optimization related problem.