Recommender systems inspired by the structure of quantum theory

Physicists use quantum models to describe the behavior of physical systems. Quantum models owe their success to their interpretability, to their relation to probabilistic models (quantization of classical models) and to their high predictive power. Beyond physics, these properties are valuable in general data science. This motivates the use of quantum models to analyze general nonphysical datasets. Here we provide both empirical and theoretical insights into the application of quantum models in data science. In the theoretical part of this paper, we firstly show that quantum models can be exponentially more efficient than probabilistic models because there exist datasets that admit low-dimensional quantum models and only exponentially high-dimensional probabilistic models. Secondly, we explain in what sense quantum models realize a useful relaxation of compressed probabilistic models. Thirdly, we show that sparse datasets admit low-dimensional quantum models and finally, we introduce a method to compute hierarchical orderings of properties of users (e.g., personality traits) and items (e.g., genres of movies). In the empirical part of the paper, we evaluate quantum models in item recommendation and observe that the predictive power of quantum-inspired recommender systems can compete with state-of-the-art recommender systems like SVD++ and PureSVD. Furthermore, we make use of the interpretability of quantum models by computing hierarchical orderings of properties of users and items. This work establishes a connection between data science (item recommendation), information theory (communication complexity), mathematical programming (positive semidefinite factorizations) and physics (quantum models).

Top-N recommendations from expressive recommender systems

Normalized nonnegative models assign probability distributions to users and random variables to items; see [Stark, 2015]. Rating an item is regarded as sampling the random variable assigned to the item with respect to the distribution assigned to the user who rates the item. Models of that kind are highly expressive. For instance, using normalized nonnegative models we can understand users' preferences as mixtures of interpretable user stereotypes, and we can arrange properties of users and items in a hierarchical manner. These features would not be useful if the predictive power of normalized nonnegative models was poor. Thus, we analyze here the performance of normalized nonnegative models for top-N recommendation and observe that their performance matches the performance of methods like PureSVD which was introduced in [Cremonesi et al., 2010]. We conclude that normalized nonnegative models not only provide accurate recommendations but they also deliver (for free) representations that are interpretable. We deepen the discussion of normalized nonnegative models by providing further theoretical insights. In particular, we introduce total variational distance as an operational similarity measure, we discover scenarios where normalized nonnegative models yield unique representations of users and items, we prove that the inference of optimal normalized nonnegative models is NP-hard and finally, we discuss the relationship between normalized nonnegative models and nonnegative matrix factorization.

Expressive recommender systems through normalized nonnegative models

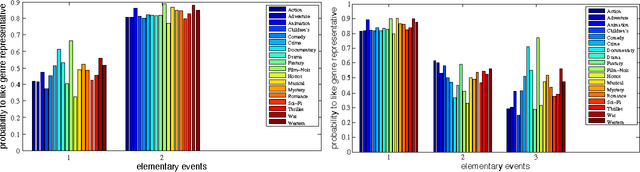
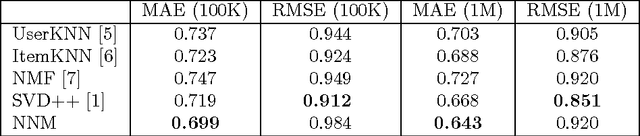
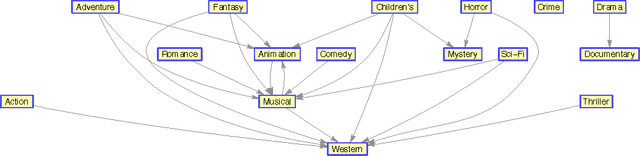
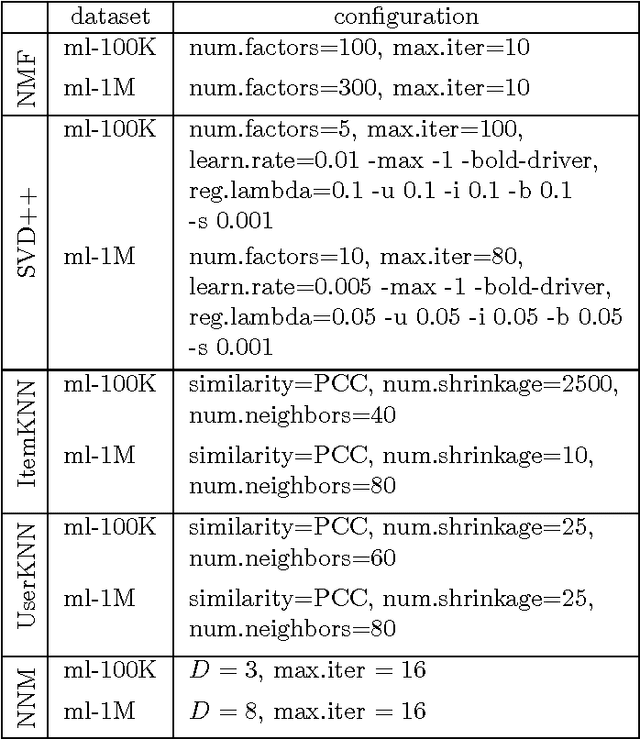
We introduce normalized nonnegative models (NNM) for explorative data analysis. NNMs are partial convexifications of models from probability theory. We demonstrate their value at the example of item recommendation. We show that NNM-based recommender systems satisfy three criteria that all recommender systems should ideally satisfy: high predictive power, computational tractability, and expressive representations of users and items. Expressive user and item representations are important in practice to succinctly summarize the pool of customers and the pool of items. In NNMs, user representations are expressive because each user's preference can be regarded as normalized mixture of preferences of stereotypical users. The interpretability of item and user representations allow us to arrange properties of items (e.g., genres of movies or topics of documents) or users (e.g., personality traits) hierarchically.