Claude-Guy Quimper
Proving Conjectures Acquired by Composing Multiple Biases
Dec 14, 2023


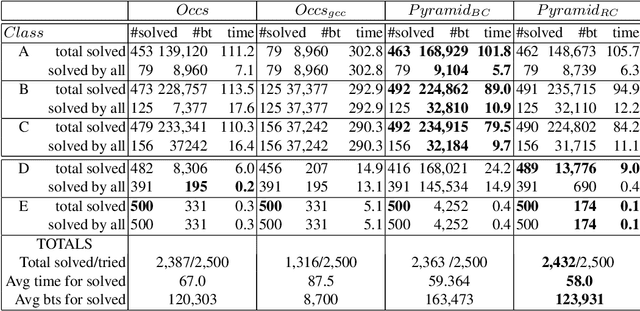
Abstract:We present the proofs of the conjectures mentioned in the paper published in the proceedings of the 2024 AAAI conference [1], and discovered by the decomposition methods presented in the same paper.
Partial Queries for Constraint Acquisition
Mar 14, 2020
Abstract:Learning constraint networks is known to require a number of membership queries exponential in the number of variables. In this paper, we learn constraint networks by asking the user partial queries. That is, we ask the user to classify assignments to subsets of the variables as positive or negative. We provide an algorithm, called QUACQ, that, given a negative example, focuses onto a constraint of the target network in a number of queries logarithmic in the size of the example. The whole constraint network can then be learned with a polynomial number of partial queries. We give information theoretic lower bounds for learning some simple classes of constraint networks and show that our generic algorithm is optimal in some cases.
Classifying Pattern and Feature Properties to Get a $Θ(n)$ Checker and Reformulation for Sliding Time-Series Constraints
Dec 03, 2019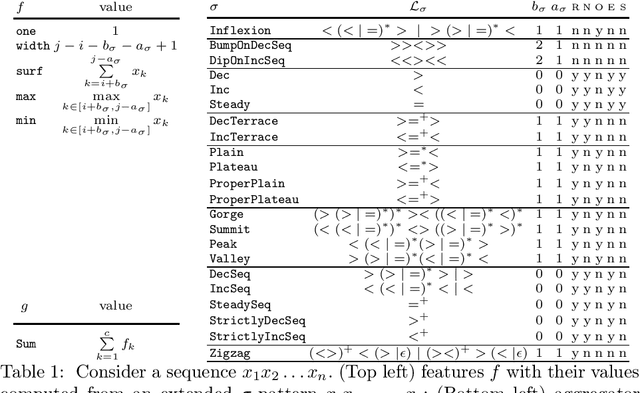

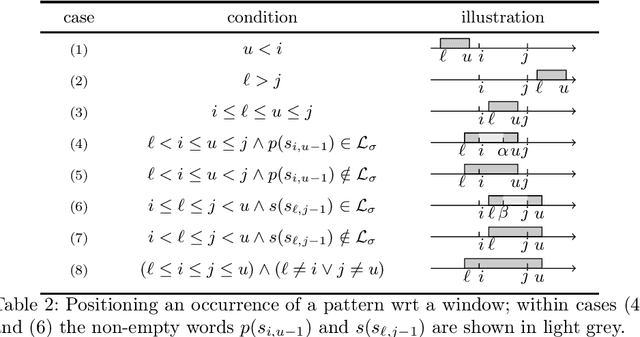
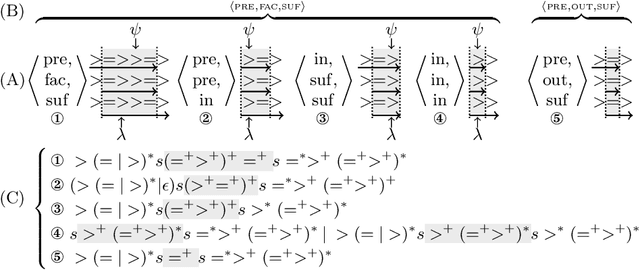
Abstract:Given, a sequence $\mathcal{X}$ of $n$ variables, a time-series constraint ctr using the Sum aggregator, and a sliding time-series constraint enforcing the constraint ctr on each sliding window of $\mathcal{X}$ of $m$ consecutive variables, we describe a $\Theta(n)$ time complexity checker, as well as a $\Theta(n)$ space complexity reformulation for such sliding constraint.
Counting-Based Search: Branching Heuristics for Constraint Satisfaction Problems
Jan 18, 2014
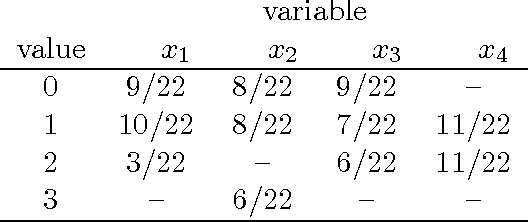
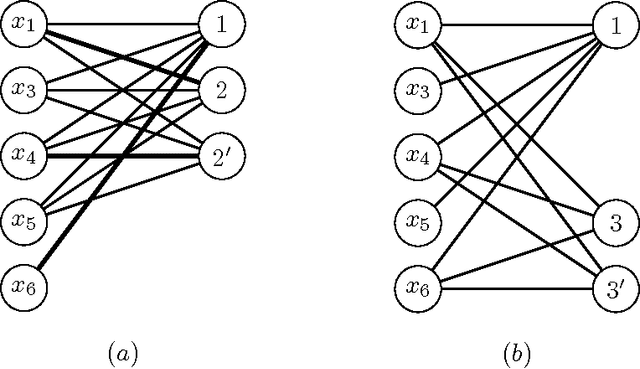
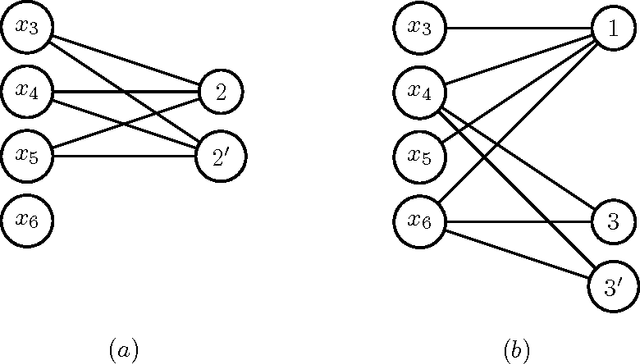
Abstract:Designing a search heuristic for constraint programming that is reliable across problem domains has been an important research topic in recent years. This paper concentrates on one family of candidates: counting-based search. Such heuristics seek to make branching decisions that preserve most of the solutions by determining what proportion of solutions to each individual constraint agree with that decision. Whereas most generic search heuristics in constraint programming rely on local information at the level of the individual variable, our search heuristics are based on more global information at the constraint level. We design several algorithms that are used to count the number of solutions to specific families of constraints and propose some search heuristics exploiting such information. The experimental part of the paper considers eight problem domains ranging from well-established benchmark puzzles to rostering and sport scheduling. An initial empirical analysis identifies heuristic maxSD as a robust candidate among our proposals.eWe then evaluate the latter against the state of the art, including the latest generic search heuristics, restarts, and discrepancy-based tree traversals. Experimental results show that counting-based search generally outperforms other generic heuristics.
The AllDifferent Constraint with Precedences
Mar 19, 2011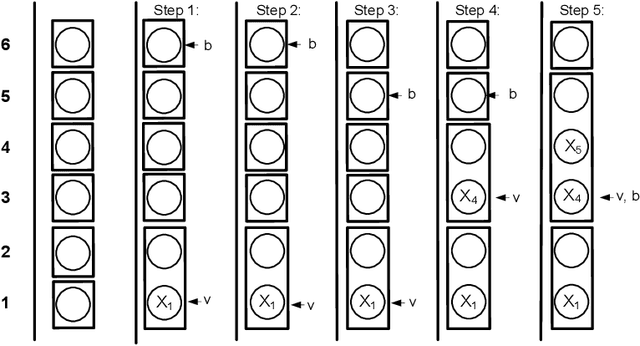
Abstract:We propose AllDiffPrecedence, a new global constraint that combines together an AllDifferent constraint with precedence constraints that strictly order given pairs of variables. We identify a number of applications for this global constraint including instruction scheduling and symmetry breaking. We give an efficient propagation algorithm that enforces bounds consistency on this global constraint. We show how to implement this propagator using a decomposition that extends the bounds consistency enforcing decomposition proposed for the AllDifferent constraint. Finally, we prove that enforcing domain consistency on this global constraint is NP-hard in general.
Decomposition of the NVALUE constraint
Jul 05, 2010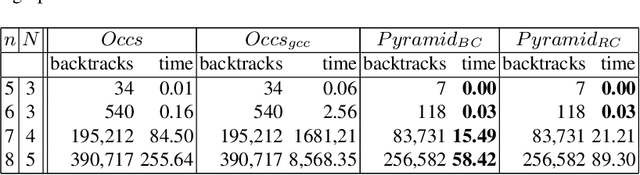
Abstract:We study decompositions of the global NVALUE constraint. Our main contribution is theoretical: we show that there are propagators for global constraints like NVALUE which decomposition can simulate with the same time complexity but with a much greater space complexity. This suggests that the benefit of a global propagator may often not be in saving time but in saving space. Our other theoretical contribution is to show for the first time that range consistency can be enforced on NVALUE with the same worst-case time complexity as bound consistency. Finally, the decompositions we study are readily encoded as linear inequalities. We are therefore able to use them in integer linear programs.
Propagating Conjunctions of AllDifferent Constraints
Apr 15, 2010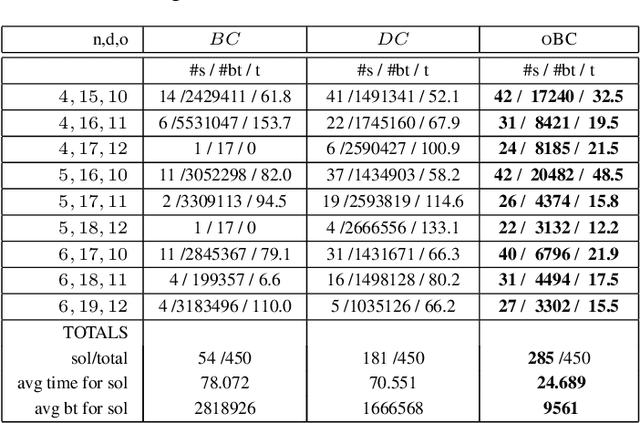
Abstract:We study propagation algorithms for the conjunction of two AllDifferent constraints. Solutions of an AllDifferent constraint can be seen as perfect matchings on the variable/value bipartite graph. Therefore, we investigate the problem of finding simultaneous bipartite matchings. We present an extension of the famous Hall theorem which characterizes when simultaneous bipartite matchings exists. Unfortunately, finding such matchings is NP-hard in general. However, we prove a surprising result that finding a simultaneous matching on a convex bipartite graph takes just polynomial time. Based on this theoretical result, we provide the first polynomial time bound consistency algorithm for the conjunction of two AllDifferent constraints. We identify a pathological problem on which this propagator is exponentially faster compared to existing propagators. Our experiments show that this new propagator can offer significant benefits over existing methods.
Flow-Based Propagators for the SEQUENCE and Related Global Constraints
Sep 24, 2009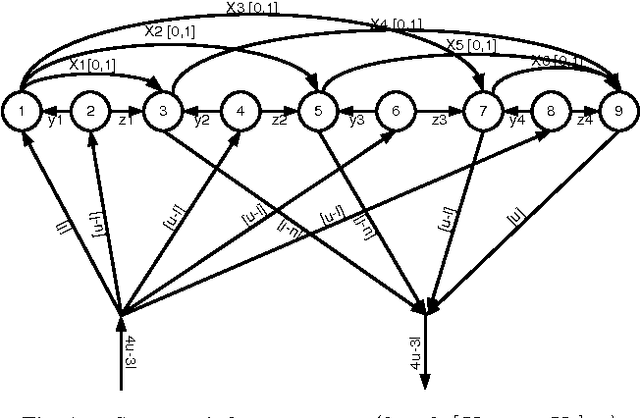
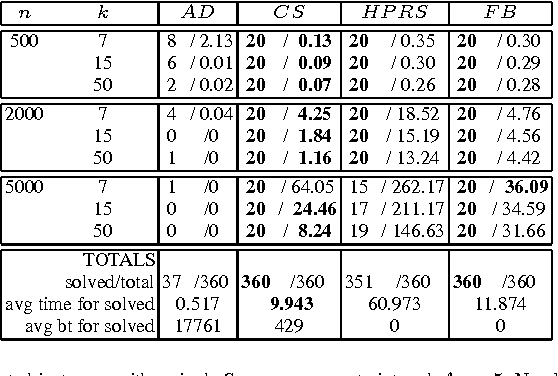
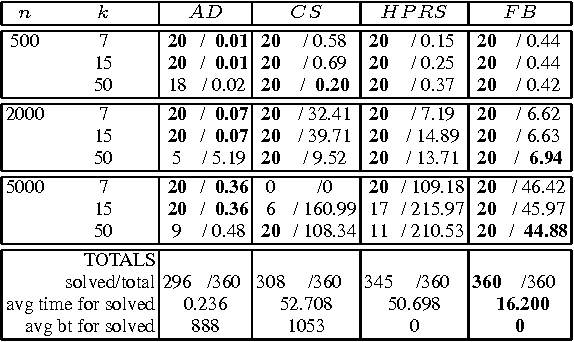
Abstract:We propose new filtering algorithms for the SEQUENCE constraint and some extensions of the SEQUENCE constraint based on network flows. We enforce domain consistency on the SEQUENCE constraint in $O(n^2)$ time down a branch of the search tree. This improves upon the best existing domain consistency algorithm by a factor of $O(\log n)$. The flows used in these algorithms are derived from a linear program. Some of them differ from the flows used to propagate global constraints like GCC since the domains of the variables are encoded as costs on the edges rather than capacities. Such flows are efficient for maintaining bounds consistency over large domains and may be useful for other global constraints.
Decompositions of All Different, Global Cardinality and Related Constraints
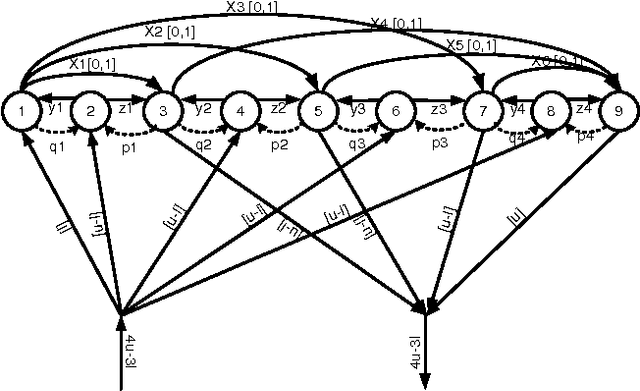
May 22, 2009
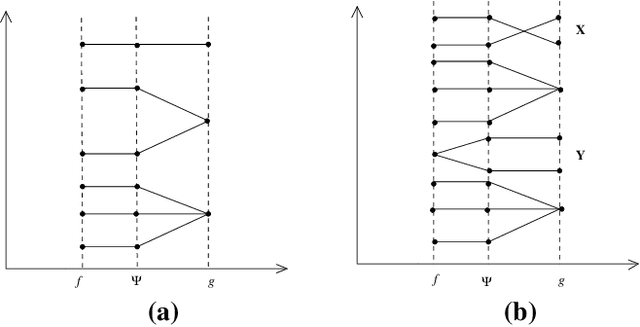
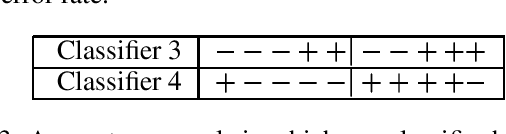
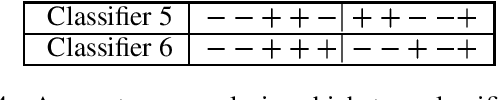
Abstract:We show that some common and important global constraints like ALL-DIFFERENT and GCC can be decomposed into simple arithmetic constraints on which we achieve bound or range consistency, and in some cases even greater pruning. These decompositions can be easily added to new solvers. They also provide other constraints with access to the state of the propagator by sharing of variables. Such sharing can be used to improve propagation between constraints. We report experiments with our decomposition in a pseudo-Boolean solver.
* Proceedings of the Twenty-first International Joint Conference on Artificial Intelligence (IJCAI-09)
Decompositions of Grammar Constraints
Mar 03, 2009Abstract:A wide range of constraints can be compactly specified using automata or formal languages. In a sequence of recent papers, we have shown that an effective means to reason with such specifications is to decompose them into primitive constraints. We can then, for instance, use state of the art SAT solvers and profit from their advanced features like fast unit propagation, clause learning, and conflict-based search heuristics. This approach holds promise for solving combinatorial problems in scheduling, rostering, and configuration, as well as problems in more diverse areas like bioinformatics, software testing and natural language processing. In addition, decomposition may be an effective method to propagate other global constraints.
* Proceedings of the Twenty-Third AAAI Conference on Artificial Intelligence
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge