Integrating overlapping datasets using bivariate causal discovery

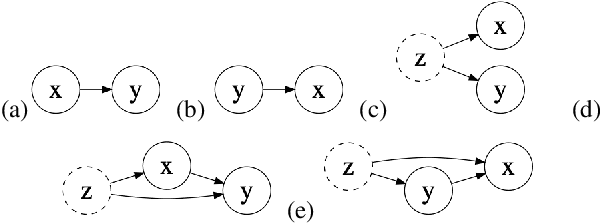
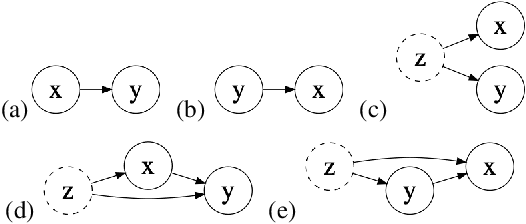
Causal knowledge is vital for effective reasoning in science, as causal relations, unlike correlations, allow one to reason about the outcomes of interventions. Algorithms that can discover causal relations from observational data are based on the assumption that all variables have been jointly measured in a single dataset. In many cases this assumption fails. Previous approaches to overcoming this shortcoming devised algorithms that returned all joint causal structures consistent with the conditional independence information contained in each individual dataset. But, as conditional independence tests only determine causal structure up to Markov equivalence, the number of consistent joint structures returned by these approaches can be quite large. The last decade has seen the development of elegant algorithms for discovering causal relations beyond conditional independence, which can distinguish among Markov equivalent structures. In this work we adapt and extend these so-called bivariate causal discovery algorithms to the problem of learning consistent causal structures from multiple datasets with overlapping variables belonging to the same generating process, providing a sound and complete algorithm that outperforms previous approaches on synthetic and real data.

Leveraging directed causal discovery to detect latent common causes

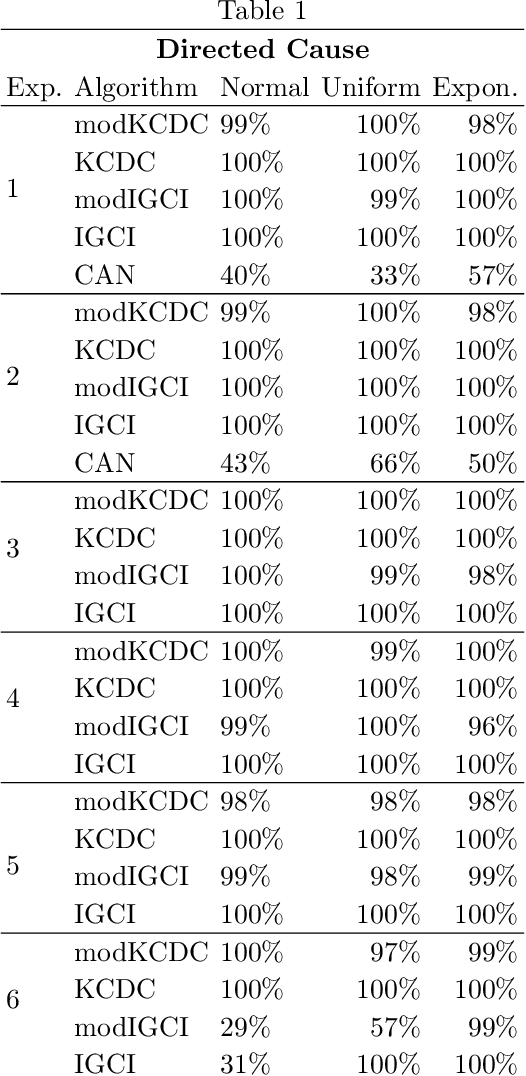
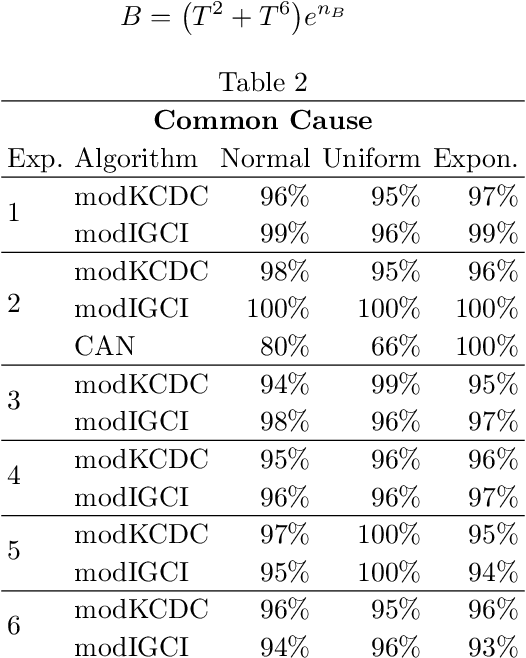
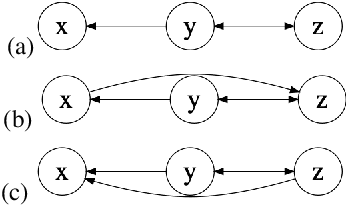
The discovery of causal relationships is a fundamental problem in science and medicine. In recent years, many elegant approaches to discovering causal relationships between two variables from uncontrolled data have been proposed. However, most of these deal only with purely directed causal relationships and cannot detect latent common causes. Here, we devise a general method which takes a purely directed causal discovery algorithm and modifies it so that it can also detect latent common causes. The identifiability of the modified algorithm depends on the identifiability of the original, as well as an assumption that the strength of noise be relatively small. We apply our method to two directed causal discovery algorithms, the Information Geometric Causal Inference of (Daniusis et al., 2010) and the Kernel Conditional Deviance for Causal Inference of (Mitrovic, Sejdinovic, and Teh, 2018), and extensively test on synthetic data---detecting latent common causes in additive, multiplicative and complex noise regimes---and on real data, where we are able to detect known common causes. In addition to detecting latent common causes, our experiments demonstrate that both modified algorithms preserve the performance of the original directed algorithm in distinguishing directed causal relations.

MultiVerse: Causal Reasoning using Importance Sampling in Probabilistic Programming

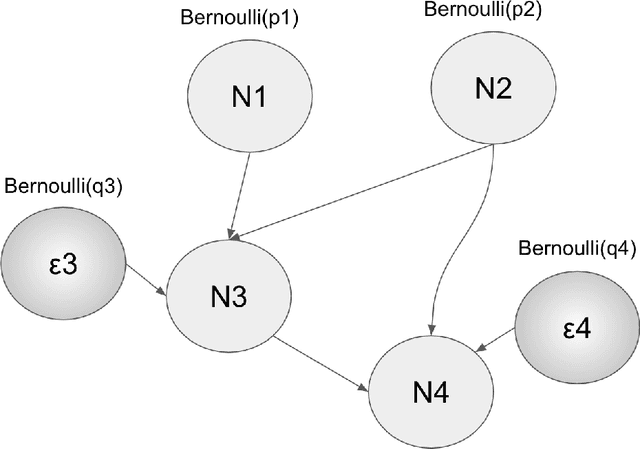
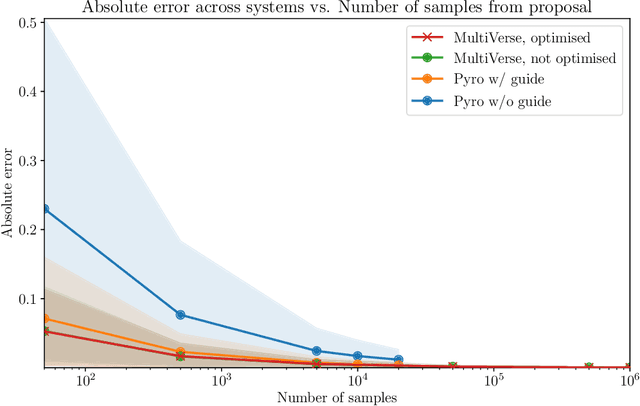
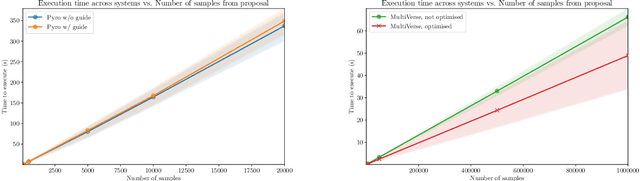
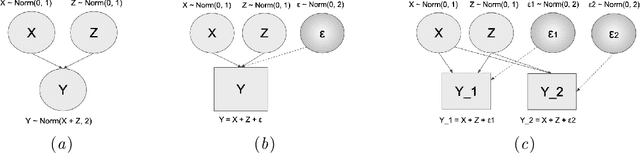
We elaborate on using importance sampling for causal reasoning, in particular for counterfactual inference. We show how this can be implemented natively in probabilistic programming. By considering the structure of the counterfactual query, one can significantly optimise the inference process. We also consider design choices to enable further optimisations. We introduce MultiVerse, a probabilistic programming prototype engine for approximate causal reasoning. We provide experimental results and compare with Pyro, an existing probabilistic programming framework with some of causal reasoning tools.

Causal inference via algebraic geometry: feasibility tests for functional causal structures with two binary observed variables

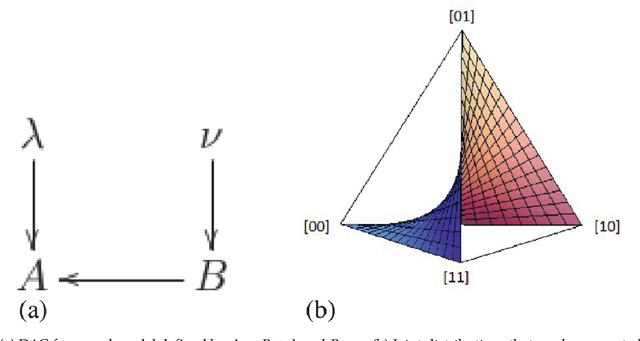
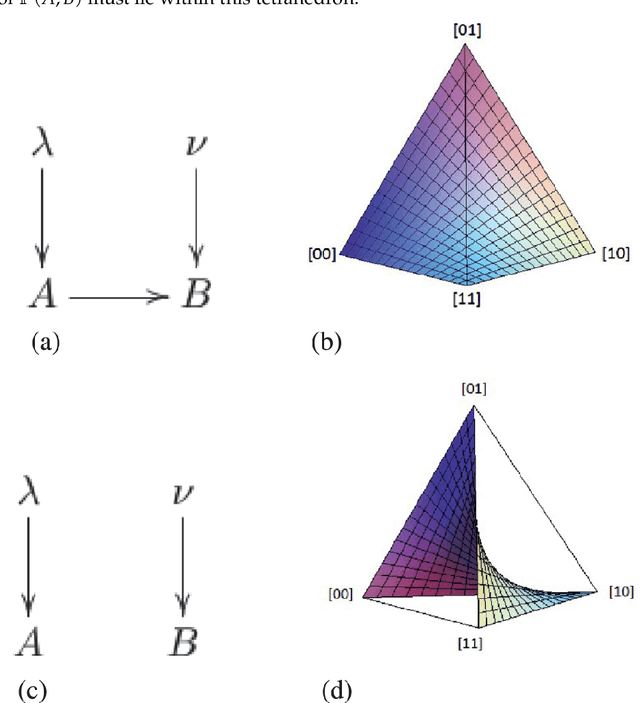
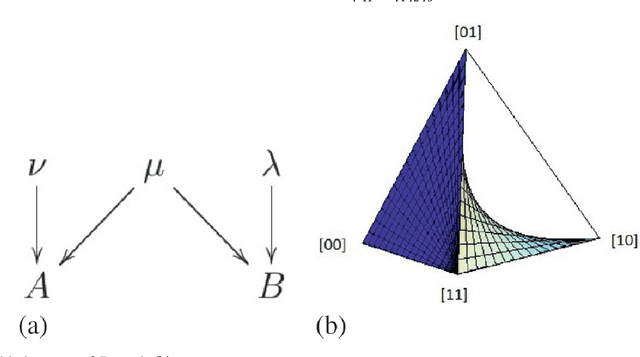
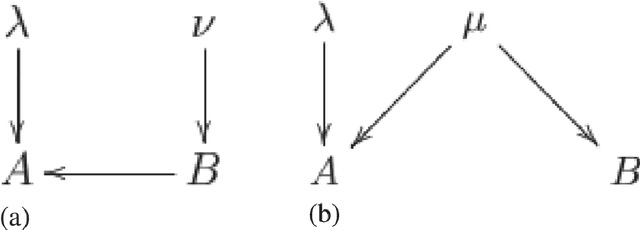
We provide a scheme for inferring causal relations from uncontrolled statistical data based on tools from computational algebraic geometry, in particular, the computation of Groebner bases. We focus on causal structures containing just two observed variables, each of which is binary. We consider the consequences of imposing different restrictions on the number and cardinality of latent variables and of assuming different functional dependences of the observed variables on the latent ones (in particular, the noise need not be additive). We provide an inductive scheme for classifying functional causal structures into distinct observational equivalence classes. For each observational equivalence class, we provide a procedure for deriving constraints on the joint distribution that are necessary and sufficient conditions for it to arise from a model in that class. We also demonstrate how this sort of approach provides a means of determining which causal parameters are identifiable and how to solve for these. Prospects for expanding the scope of our scheme, in particular to the problem of quantum causal inference, are also discussed.