Online learning to accelerate nonlinear PDE solvers: applied to multiphase porous media flow

We propose a novel type of nonlinear solver acceleration for systems of nonlinear partial differential equations (PDEs) that is based on online/adaptive learning. It is applied in the context of multiphase flow in porous media. The proposed method rely on four pillars: (i) dimensionless numbers as input parameters for the machine learning model, (ii) simplified numerical model (two-dimensional) for the offline training, (iii) dynamic control of a nonlinear solver tuning parameter (numerical relaxation), (iv) and online learning for real-time improvement of the machine learning model. This strategy decreases the number of nonlinear iterations by dynamically modifying a single global parameter, the relaxation factor, and by adaptively learning the attributes of each numerical model on-the-run. Furthermore, this work performs a sensitivity study in the dimensionless parameters (machine learning features), assess the efficacy of various machine learning models, demonstrate a decrease in nonlinear iterations using our method in more intricate, realistic three-dimensional models, and fully couple a machine learning model into an open-source multiphase flow simulator achieving up to 85\% reduction in computational time.

Data Assimilation Predictive GAN (DA-PredGAN): applied to determine the spread of COVID-19

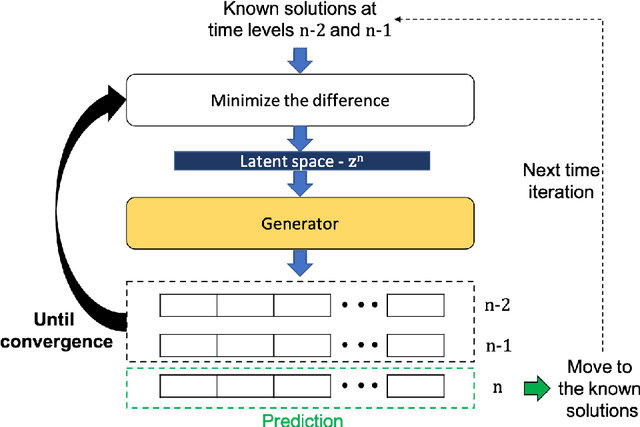
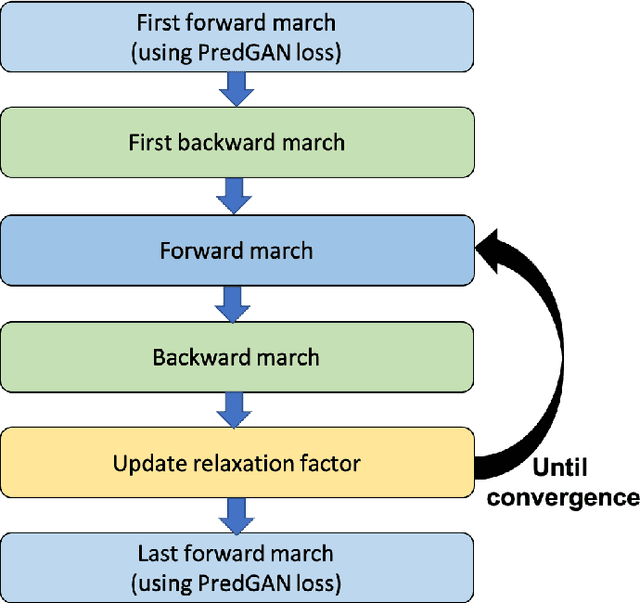
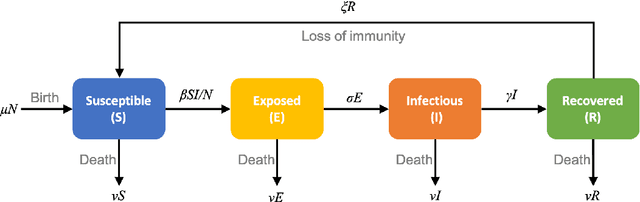
We propose the novel use of a generative adversarial network (GAN) (i) to make predictions in time (PredGAN) and (ii) to assimilate measurements (DA-PredGAN). In the latter case, we take advantage of the natural adjoint-like properties of generative models and the ability to simulate forwards and backwards in time. GANs have received much attention recently, after achieving excellent results for their generation of realistic-looking images. We wish to explore how this property translates to new applications in computational modelling and to exploit the adjoint-like properties for efficient data assimilation. To predict the spread of COVID-19 in an idealised town, we apply these methods to a compartmental model in epidemiology that is able to model space and time variations. To do this, the GAN is set within a reduced-order model (ROM), which uses a low-dimensional space for the spatial distribution of the simulation states. Then the GAN learns the evolution of the low-dimensional states over time. The results show that the proposed methods can accurately predict the evolution of the high-fidelity numerical simulation, and can efficiently assimilate observed data and determine the corresponding model parameters.