Proceedings of the 2024 XCSP3 Competition

This document represents the proceedings of the 2024 XCSP3 Competition. The results of this competition of constraint solvers were presented at CP'24 (30th International Conference on Principles and Practice of Constraint Programming).

Proceedings of the 2023 XCSP3 Competition

This document represents the proceedings of the 2023 XCSP3 Competition. The results of this competition of constraint solvers were presented at CP'23 (the 29th International Conference on Principles and Practice of Constraint Programming, held in Toronto, Canada from 27th to 31th August, 2023).

Proceedings of the 2022 XCSP3 Competition

This document represents the proceedings of the 2022 XCSP3 Competition. The results of this competition of constraint solvers were presented at FLOC (Federated Logic Conference) 2022 Olympic Games, held in Haifa, Israel from 31th July 2022 to 7th August, 2022.

XCSP3-core: A Format for Representing Constraint Satisfaction/Optimization Problems

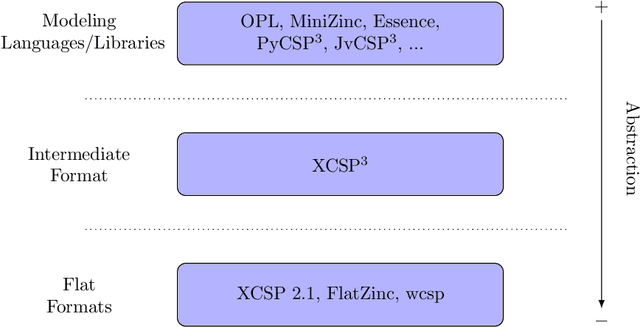
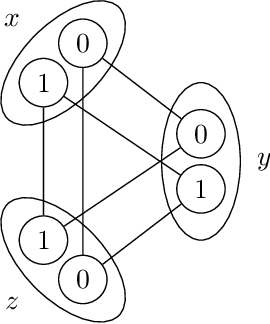
In this document, we introduce XCSP3-core, a subset of XCSP3 that allows us to represent constraint satisfaction/optimization problems. The interest of XCSP3-core is multiple: (i) focusing on the most popular frameworks (CSP and COP) and constraints, (ii) facilitating the parsing process by means of dedicated XCSP3-core parsers written in Java and C++ (using callback functions), (iii) and defining a core format for comparisons (competitions) of constraint solvers.

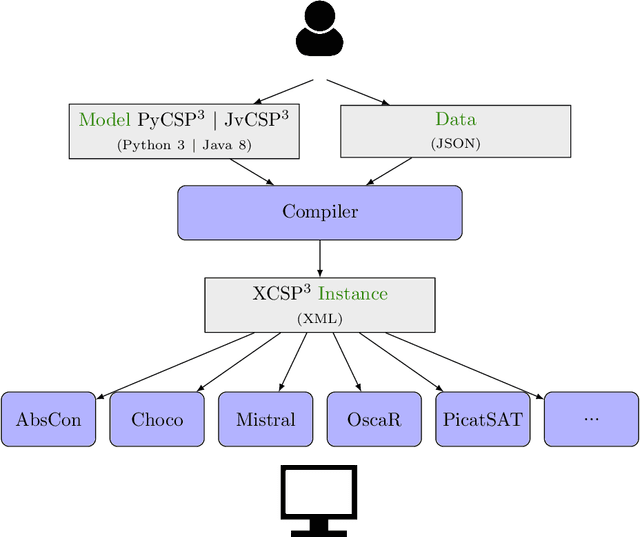
PYCSP3: Modeling Combinatorial Constrained Problems in Python

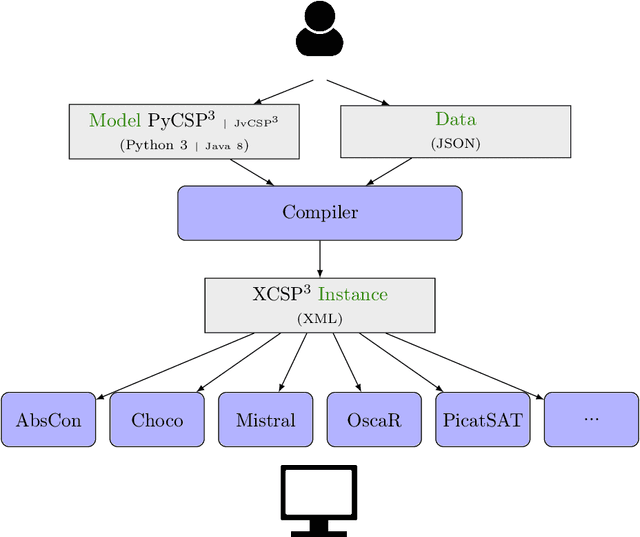
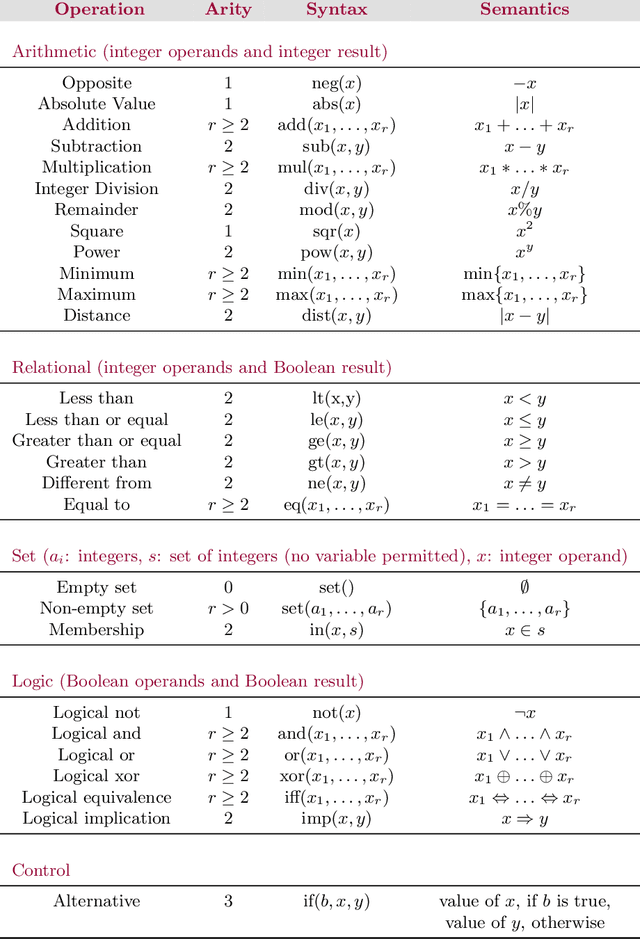
In this document, we introduce PYCSP$3$, a Python library that allows us to write models of combinatorial constrained problems in a simple and declarative way. Currently, with PyCSP$3$, you can write models of constraint satisfaction and optimization problems. More specifically, you can build CSP (Constraint Satisfaction Problem) and COP (Constraint Optimization Problem) models. Importantly, there is a complete separation between modeling and solving phases: you write a model, you compile it (while providing some data) in order to generate an XCSP3 instance (file), and you solve that problem instance by means of a constraint solver. In this document, you will find all that you need to know about PYCSP$3$, with more than 40 illustrative models.

Proceedings of the 2018 XCSP3 Competition

This document represents the proceedings of the 2018 XCSP3 Competition. The results of this competition of constraint solvers were presented at CP'18, the 24th International Conference on Principles and Practice of Constraint Programming, held in Lille, France from 27th August 2018 to 31th August, 2018.

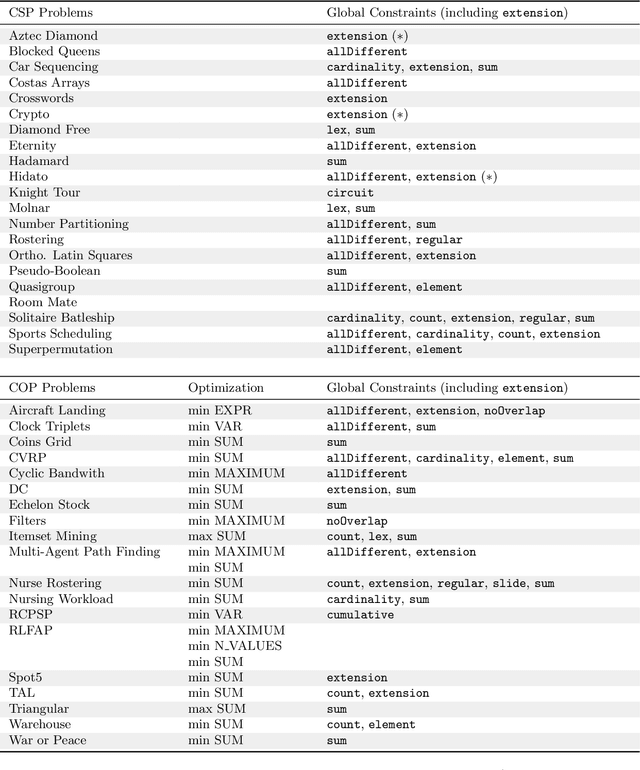
XCSP3: An Integrated Format for Benchmarking Combinatorial Constrained Problems

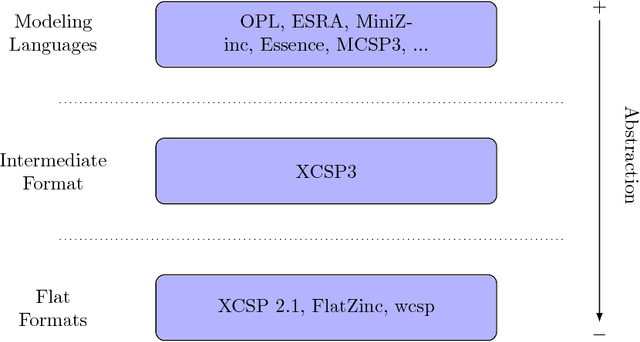
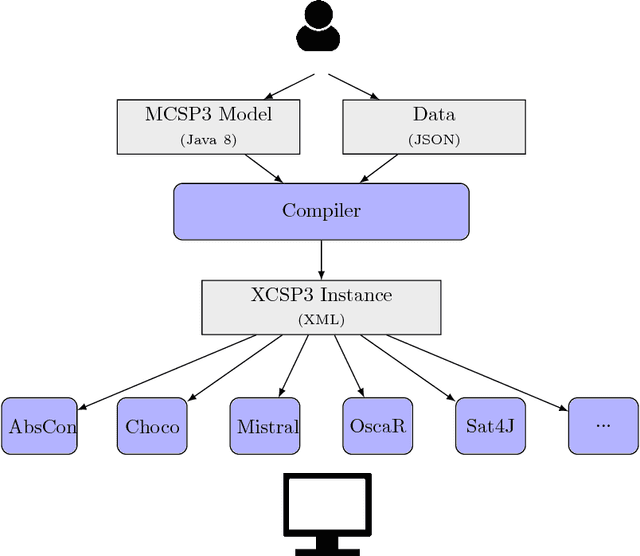
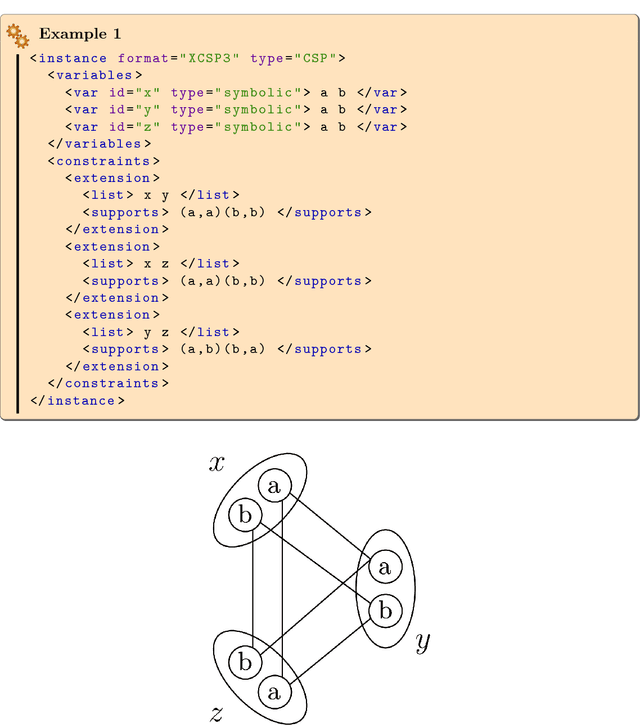
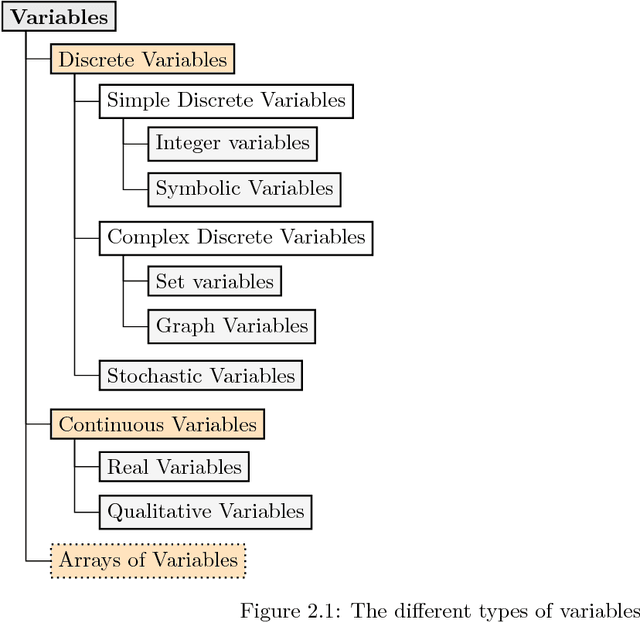
We propose a major revision of the format XCSP 2.1, called XCSP3, to build integrated representations of combinatorial constrained problems. This new format is able to deal with mono/multi optimization, many types of variables, cost functions, reification, views, annotations, variable quantification, distributed, probabilistic and qualitative reasoning. The new format is made compact, highly readable, and rather easy to parse. Interestingly, it captures the structure of the problem models, through the possibilities of declaring arrays of variables, and identifying syntactic and semantic groups of constraints. The number of constraints is kept under control by introducing a limited set of basic constraint forms, and producing almost automatically some of their variations through lifting, restriction, sliding, logical combination and relaxation mechanisms. As a result, XCSP3 encompasses practically all constraints that can be found in major constraint solvers developed by the CP community. A website, which is developed conjointly with the format, contains many models and series of instances. The user can make sophisticated queries for selecting instances from very precise criteria. The objective of XCSP3 is to ease the effort required to test and compare different algorithms by providing a common test-bed of combinatorial constrained instances.

Compact-Table: Efficiently Filtering Table Constraints with Reversible Sparse Bit-Sets

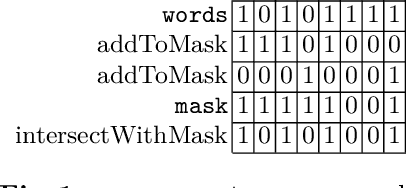
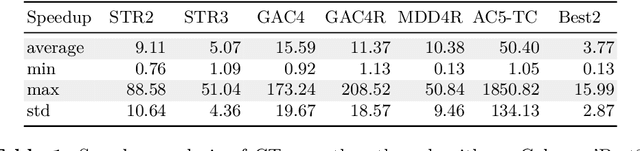
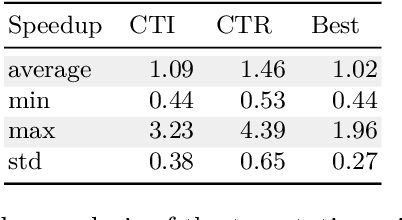
In this paper, we describe Compact-Table (CT), a bitwise algorithm to enforce Generalized Arc Consistency (GAC) on table con- straints. Although this algorithm is the default propagator for table constraints in or-tools and OscaR, two publicly available CP solvers, it has never been described so far. Importantly, CT has been recently improved further with the introduction of residues, resetting operations and a data-structure called reversible sparse bit-set, used to maintain tables of supports (following the idea of tabular reduction): tuples are invalidated incrementally on value removals by means of bit-set operations. The experimentation that we have conducted with OscaR shows that CT outperforms state-of-the-art algorithms STR2, STR3, GAC4R, MDD4R and AC5-TC on standard benchmarks.

Second-Order Consistencies

In this paper, we propose a comprehensive study of second-order consistencies (i.e., consistencies identifying inconsistent pairs of values) for constraint satisfaction. We build a full picture of the relationships existing between four basic second-order consistencies, namely path consistency (PC), 3-consistency (3C), dual consistency (DC) and 2-singleton arc consistency (2SAC), as well as their conservative and strong variants. Interestingly, dual consistency is an original property that can be established by using the outcome of the enforcement of generalized arc consistency (GAC), which makes it rather easy to obtain since constraint solvers typically maintain GAC during search. On binary constraint networks, DC is equivalent to PC, but its restriction to existing constraints, called conservative dual consistency (CDC), is strictly stronger than traditional conservative consistencies derived from path consistency, namely partial path consistency (PPC) and conservative path consistency (CPC). After introducing a general algorithm to enforce strong (C)DC, we present the results of an experimentation over a wide range of benchmarks that demonstrate the interest of (conservative) dual consistency. In particular, we show that enforcing (C)DC before search clearly improves the performance of MAC (the algorithm that maintains GAC during search) on several binary and non-binary structured problems.

Solving WCSP by Extraction of Minimal Unsatisfiable Cores

Usual techniques to solve WCSP are based on cost transfer operations coupled with a branch and bound algorithm. In this paper, we focus on an approach integrating extraction and relaxation of Minimal Unsatisfiable Cores in order to solve this problem. We decline our approach in two ways: an incomplete, greedy, algorithm and a complete one.