High Dimensional Time Series Regression Models: Applications to Statistical Learning Methods

These lecture notes provide an overview of existing methodologies and recent developments for estimation and inference with high dimensional time series regression models. First, we present main limit theory results for high dimensional dependent data which is relevant to covariance matrix structures as well as to dependent time series sequences. Second, we present main aspects of the asymptotic theory related to time series regression models with many covariates. Third, we discuss various applications of statistical learning methodologies for time series analysis purposes.

Forecast Evaluation in Large Cross-Sections of Realized Volatility

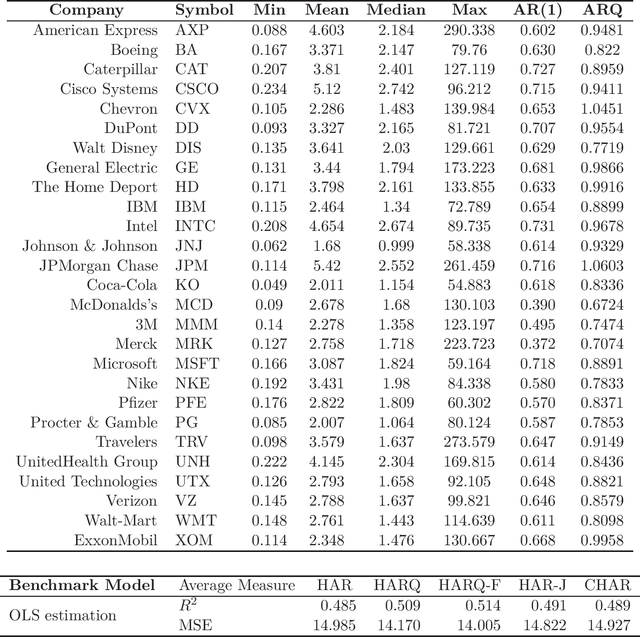
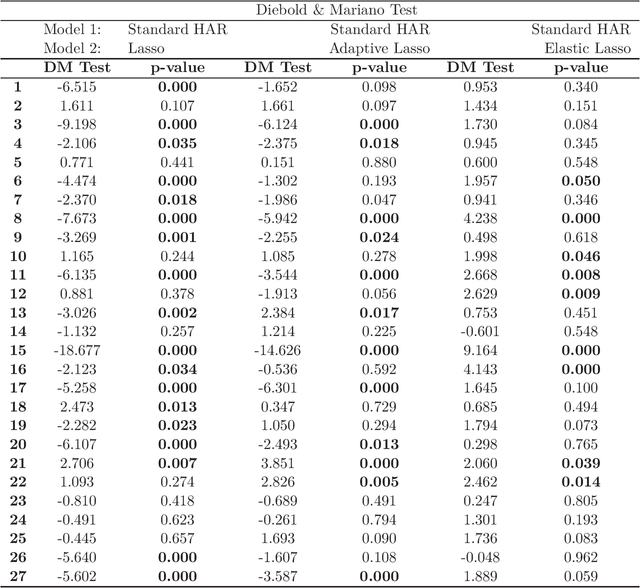
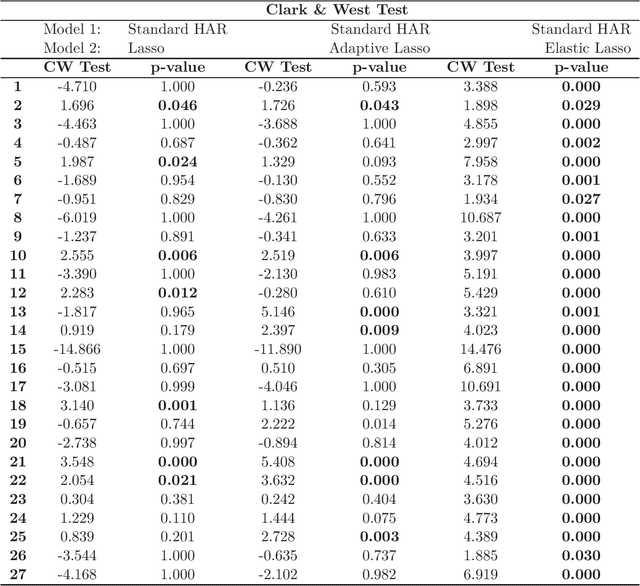
In this paper, we consider the forecast evaluation of realized volatility measures under cross-section dependence using equal predictive accuracy testing procedures. We evaluate the predictive accuracy of the model based on the augmented cross-section when forecasting Realized Volatility. Under the null hypothesis of equal predictive accuracy the benchmark model employed is a standard HAR model while under the alternative of non-equal predictive accuracy the forecast model is an augmented HAR model estimated via the LASSO shrinkage. We study the sensitivity of forecasts to the model specification by incorporating a measurement error correction as well as cross-sectional jump component measures. The out-of-sample forecast evaluation of the models is assessed with numerical implementations.