Dynamics of Supervised and Reinforcement Learning in the Non-Linear Perceptron

The ability of a brain or a neural network to efficiently learn depends crucially on both the task structure and the learning rule. Previous works have analyzed the dynamical equations describing learning in the relatively simplified context of the perceptron under assumptions of a student-teacher framework or a linearized output. While these assumptions have facilitated theoretical understanding, they have precluded a detailed understanding of the roles of the nonlinearity and input-data distribution in determining the learning dynamics, limiting the applicability of the theories to real biological or artificial neural networks. Here, we use a stochastic-process approach to derive flow equations describing learning, applying this framework to the case of a nonlinear perceptron performing binary classification. We characterize the effects of the learning rule (supervised or reinforcement learning, SL/RL) and input-data distribution on the perceptron's learning curve and the forgetting curve as subsequent tasks are learned. In particular, we find that the input-data noise differently affects the learning speed under SL vs. RL, as well as determines how quickly learning of a task is overwritten by subsequent learning. Additionally, we verify our approach with real data using the MNIST dataset. This approach points a way toward analyzing learning dynamics for more-complex circuit architectures.

Distinguishing Learning Rules with Brain Machine Interfaces

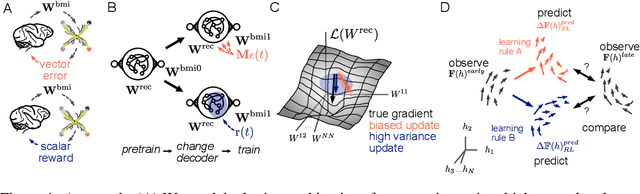
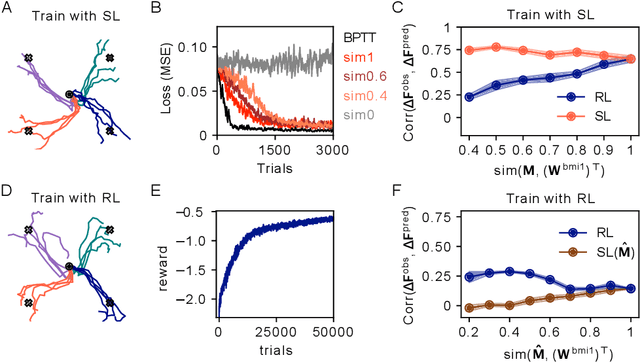
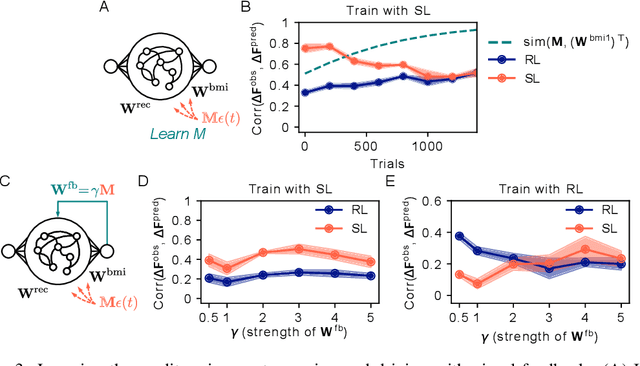
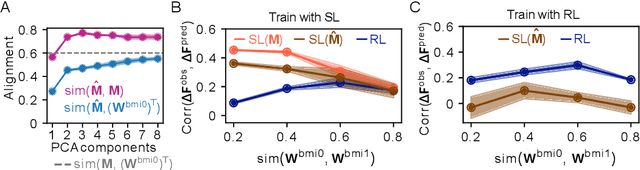
Despite extensive theoretical work on biologically plausible learning rules, it has been difficult to obtain clear evidence about whether and how such rules are implemented in the brain. We consider biologically plausible supervised- and reinforcement-learning rules and ask whether changes in network activity during learning can be used to determine which learning rule is being used. Supervised learning requires a credit-assignment model estimating the mapping from neural activity to behavior, and, in a biological organism, this model will inevitably be an imperfect approximation of the ideal mapping, leading to a bias in the direction of the weight updates relative to the true gradient. Reinforcement learning, on the other hand, requires no credit-assignment model and tends to make weight updates following the true gradient direction. We derive a metric to distinguish between learning rules by observing changes in the network activity during learning, given that the mapping from brain to behavior is known by the experimenter. Because brain-machine interface (BMI) experiments allow for perfect knowledge of this mapping, we focus on modeling a cursor-control BMI task using recurrent neural networks, showing that learning rules can be distinguished in simulated experiments using only observations that a neuroscience experimenter would plausibly have access to.